CV技术指南 | ICCV 2025 | Converse2D | 即插即用 | 卷积真正的逆 | 在图像恢复中的逆卷积

本文来源公众号“CV技术指南”，仅用于学术分享，侵权删，干货满满。

原文链接：ICCV 2025 | Converse2D | 即插即用 | 卷积真正的逆 | 在图像恢复中的逆卷积

前言 本文将逆卷积过程转为求解正则化最小二乘优化问题，引入正则化解决问题的不适定性，通过构建维纳滤波模型引入频域通过圆形边界条件求封闭解。

论文题目：Reverse Convolution and Its Applications to Image Restoration

论文链接：https://arxiv.org/pdf/2508.09824 

论文源码：https://github.com/cszn/ConverseNet

文章类型：结构创新型。

具体分类：卷积算子创新。

前置知识：卷积，反卷积，维纳滤波（Wiener Filter），最小二乘问题求解，正则化。

Motivation：下采样会造成信息丢失，卷积的逆问题又具有不适定性，为了创新卷积算子，找到卷积真正的逆运算

Method

• 卷积a、反卷积b、逆卷积c示意图。标准卷积和转置卷积将核应用于输入，但反向卷积将核应用于输出来重建输入。

  

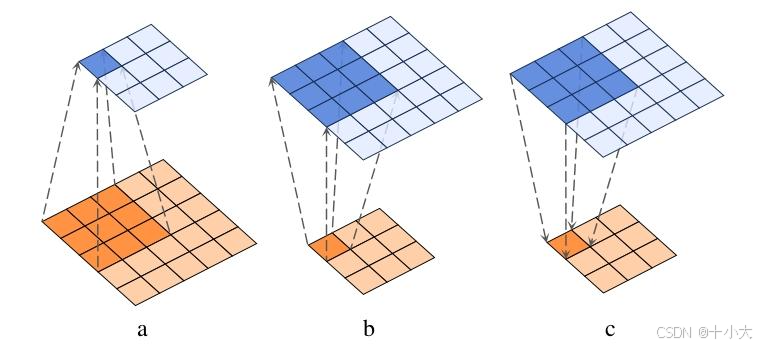
• 正向卷积过程：

  

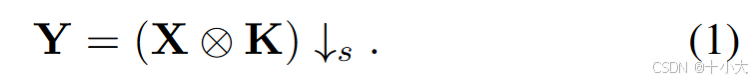
• 目的是求解X，转化为最小二乘问题：

  

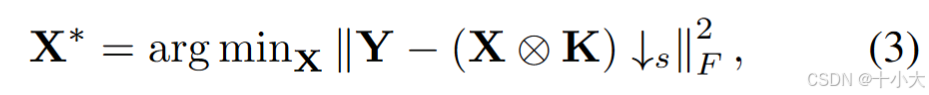
• 但问题具有不适定性，直接求解上述方程会导致不稳定的解。于是添加二次正则化项：

  

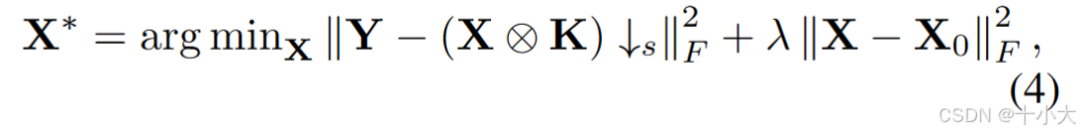
• 根据源码，X0由最近邻插值计算，控制权重参数由如下公式计算：

  

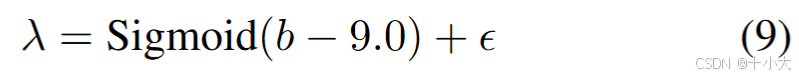
• 在卷积的圆形边界条件的假设下得到X的闭式解：

  

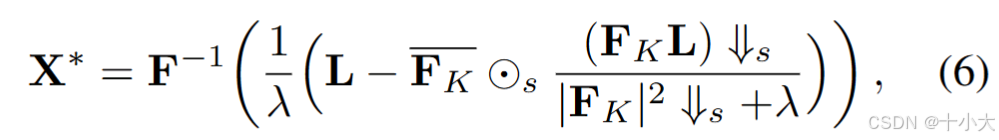
简化为（维纳滤波（Wiener Filter） 的频域形式，用于从降质观测信号中恢复真实信号）：

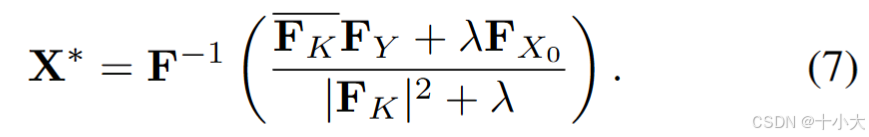
• F是快速傅里叶变换；

• FK：降质核（点扩散函数，PSF） 的傅里叶变换（即光学传递函数，OTF）；

• FY是观测信号（降质图像） 的傅里叶变换；

• FX0（插值后的低分辨率图像） 的傅里叶变换；

• FK_bar：FK的共轭（频域逆操作的核心）；

• 算法流程：

  

• Converse2D一些细节：

• 模糊核K：在预处理过程中对K应用Softmax归一化，以强制非负性和求和为一的约束；

• padding：模式为圆形填充(circular)，填充大小为4×4最优；

• X0初始化：零初始化不如插值初始化；

• Converse2D  Block：在新算子的基础上提出一个Trans-style Block，Converse2D可以增强中间特征

  

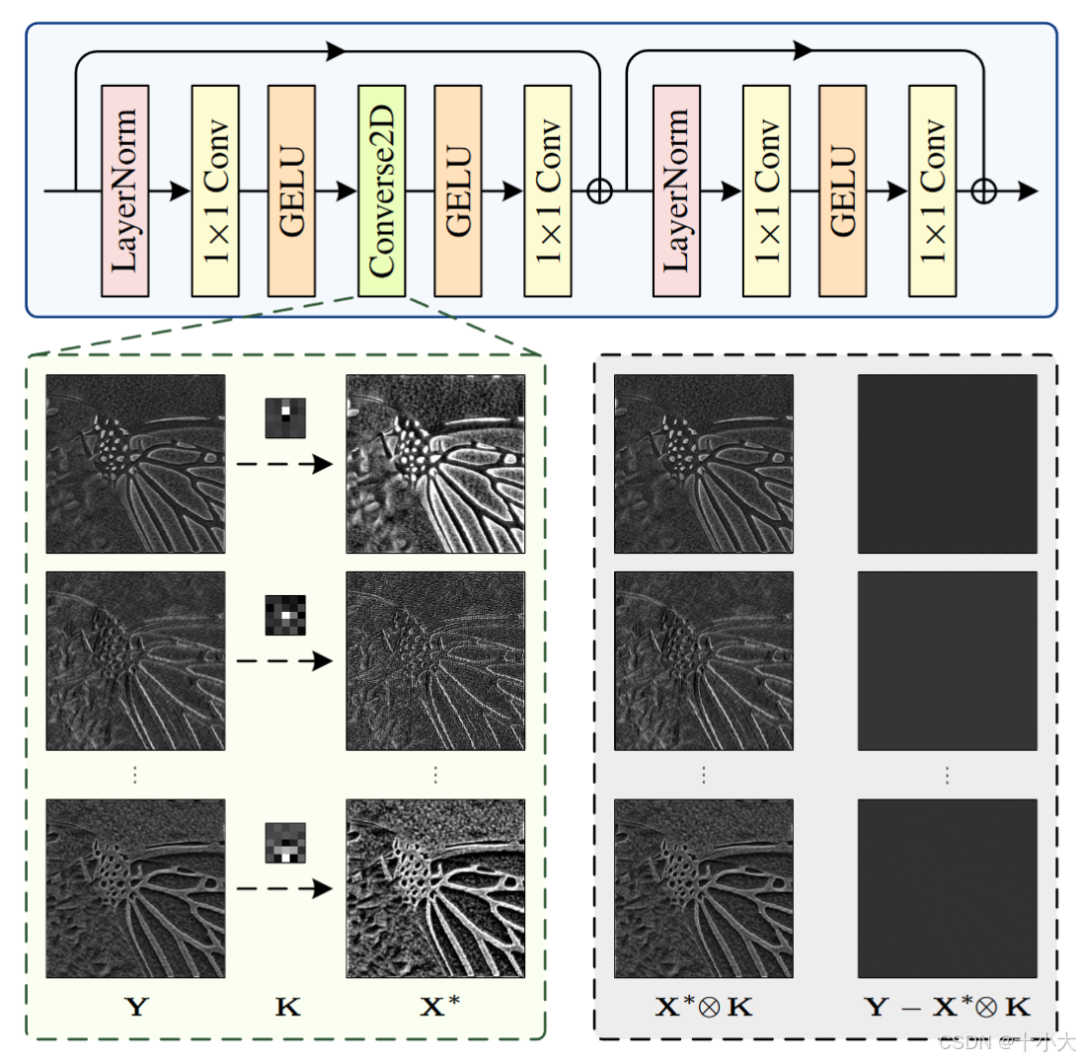
• 用Converse Block构建三种任务的网络：

  

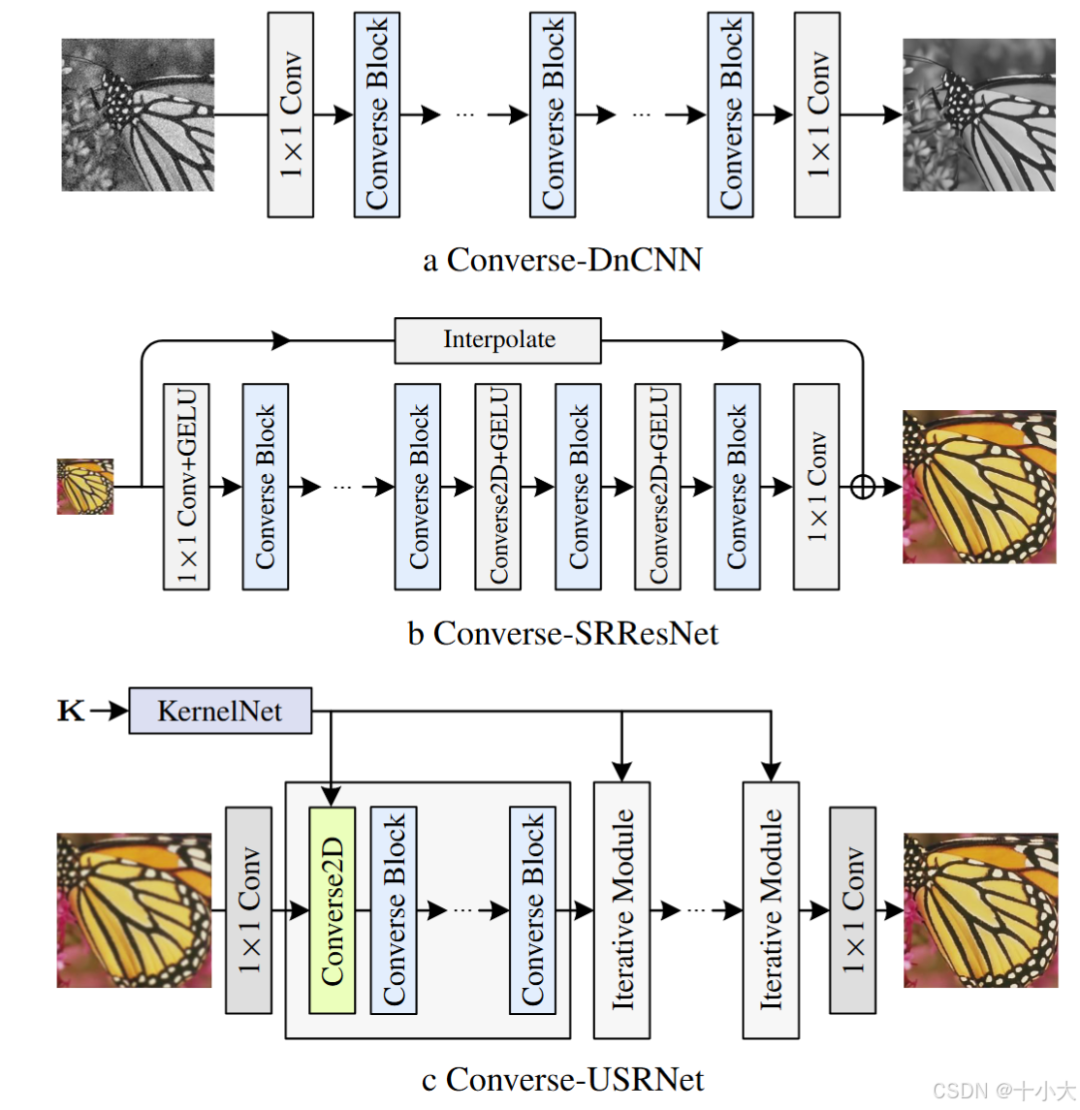
Experiment

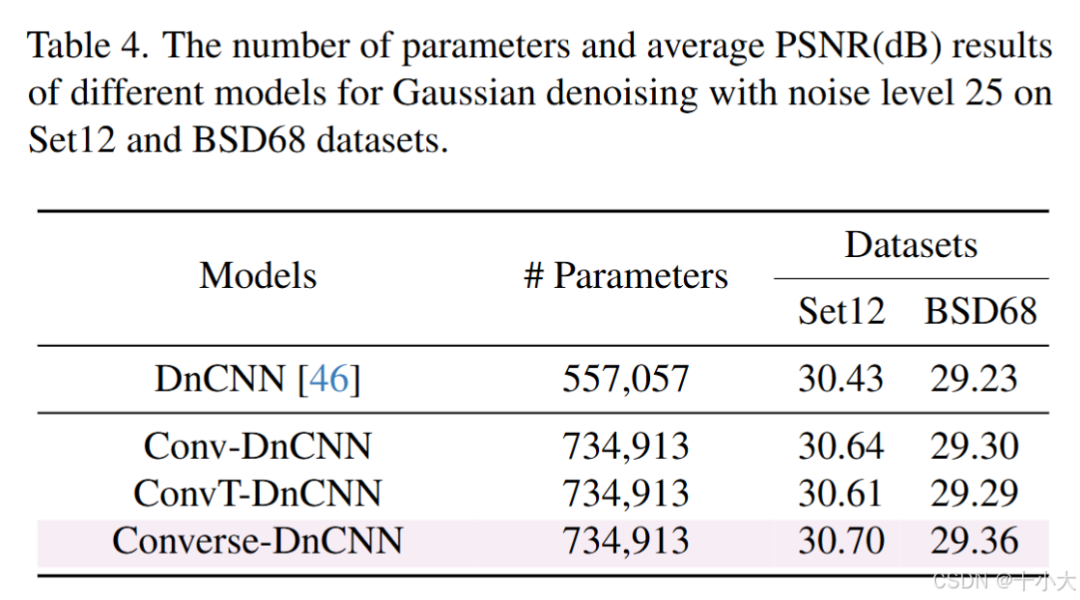
去噪：Converse2d替代传统卷积核反卷积都有提升

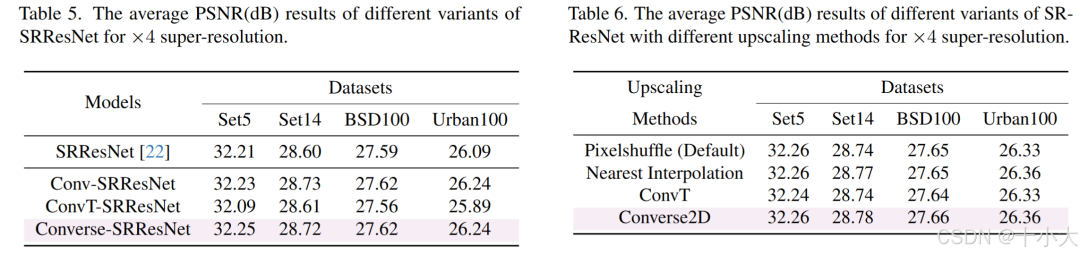
超分：替换卷积和上采样性能近似

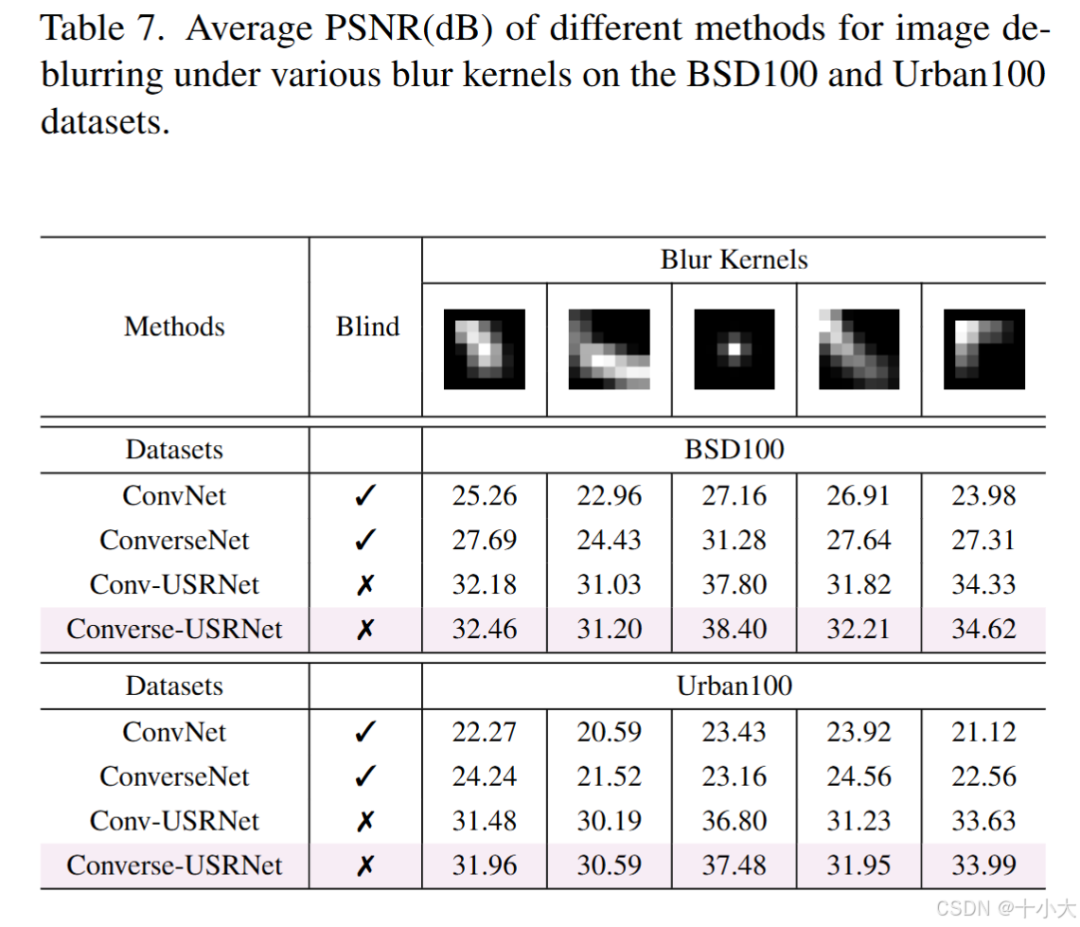
去模糊：去模糊任务不同的模糊核提升都很明显

总结与思考

• Converse2d是寻找真正的卷积逆运算的一次探索尝试，这样基础算子研究应该被予以重视和尊重；

• Converse2d在去模糊任务上提升明显，去噪有提升，超分几乎一致；

• Converse2d是一个即插即用的架构，它适用于中间特征通道数不变的位置来增强特征（图2以及源码中的输入输出通道数相同的断言）；

参考文献Bib格式

@inproceedings{huang2025reverse,

    title={Reverse Convolution and Its Applications to Image Restoration},

    author={Huang, Xuhong and Liu, Shiqi and Zhang, Kai and Tai, Ying and Yang, Jian and Zeng, Hui and Zhang, Lei},

    booktitle={International Conference on Computer Vision},

    pages={1--10},

    year={2025}

}

THE END !

文章结束，感谢阅读。您的点赞，收藏，评论是我继续更新的动力。大家有推荐的公众号可以评论区留言，共同学习，一起进步。