算法进阶 | 一文归纳常用数据结构与算法（推荐收藏！）

本文来源公众号“算法进阶”，仅用于学术分享，侵权删，干货满满。

原文链接：一文归纳常用数据结构与算法

一、 前言

程序员，也就是"通过编码操作数据容器构建起数字世界的总工程师"，从这角度看，数据结构及算法是构建虚拟世界的一系列基础的元件及方法。

平时工程中，虽然都有大量现成“轮子”可以用，但学习数据结构和算法的重要性也是毋庸置疑的：

• 可以提升逻辑思维能力：数据结构和算法蕴含着经典的抽象化问题、解决问题的思路，有利于锻炼逻辑思维。

• 可以提高编码质量：利于建立时间复杂度、空间复杂度意识，写出高质量的代码，能够设计基础架构，提升编程技能。

• 面试必备：大厂很注重考察数据结构与算法这类基础知识。相比短期能力，他们更看中你的长期潜力。特别是对于校招的项目经验不足的童鞋。

我们学习数据结构和算法，可以了解它特性、适用的场景以及它能解决的问题。结合面试及工作需要，以下总结了最常用的、最基础数据结构与算法思想：

• 数据结构：数组、链表、栈、队列、散列表、二叉树、Trie 树、堆、跳表、图

• 算法思想：递归、贪心算法、分治算法、回溯算法、动态规划

二、 基础概念

2.1 复杂度分析

关于数据结构与算法，首先要掌握一个核心概念：复杂度分析。

数据结构和算法解决的是如何更省、更快地存储和处理数据的问题，因此我们就需要一个考量数据结构与算法时间、空间复杂度的方法--大 O 复杂度表示法。常见的复杂度量级从低阶到高阶有：O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )：

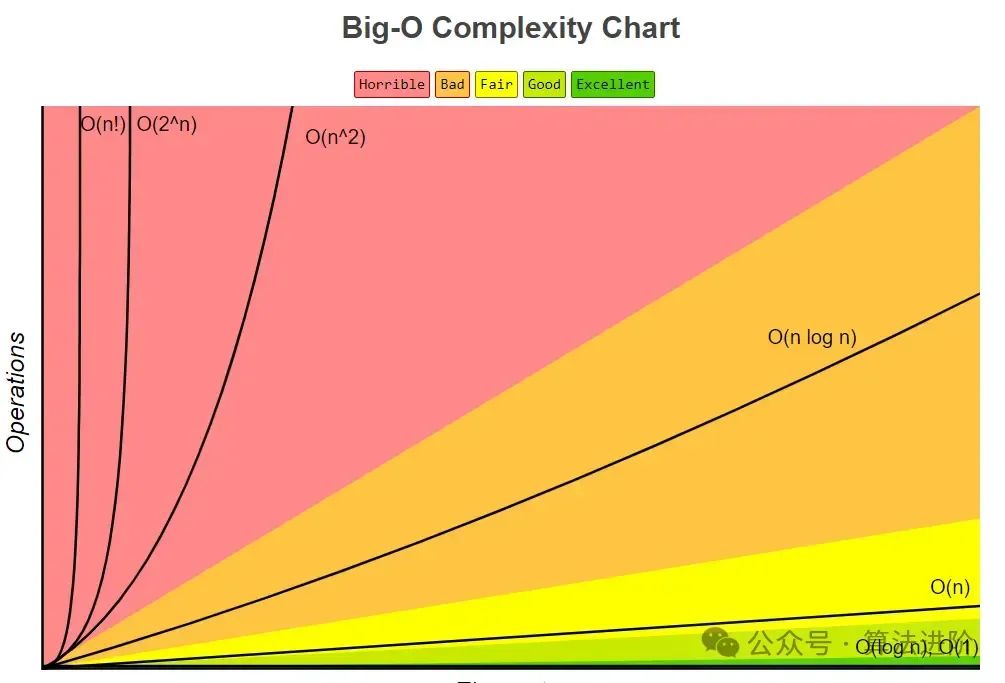
大 O 时间复杂度全称渐进时间复杂度（asymptotic time complexity），实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模(n)增长的变化趋势。同样的，空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示代码执行的存储空间与数据规模(n)之间的增长关系。

• 常见数据结构操作的复杂度：

  

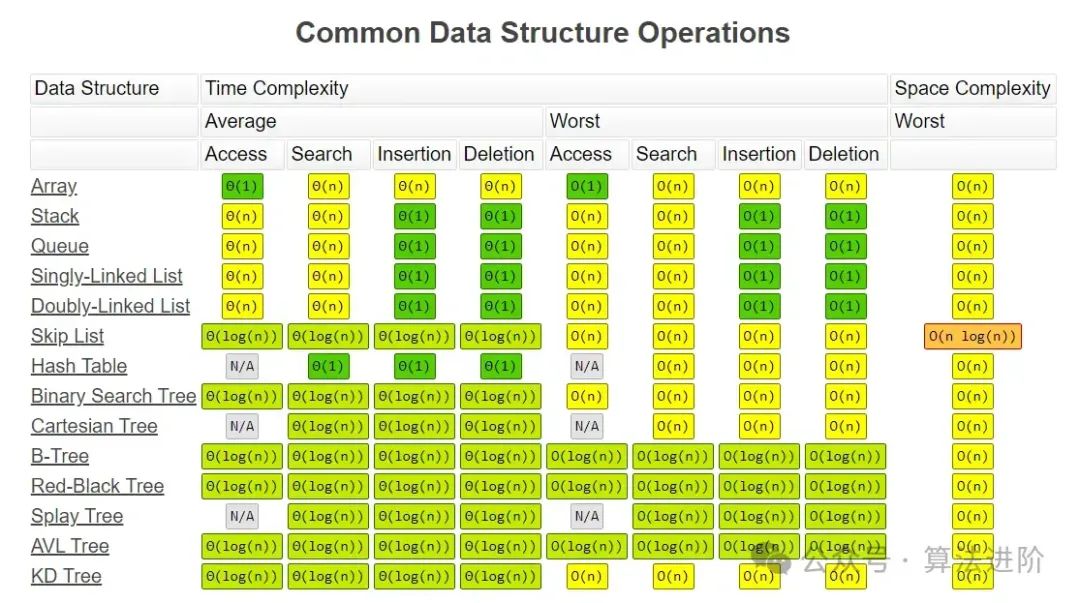
• 常见排序算法执行的复杂度：

  

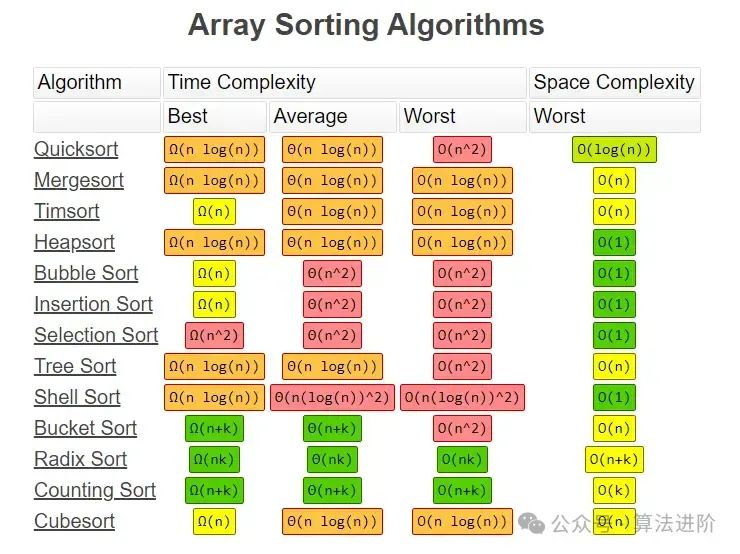
2.2 常用的数据结构与算法概览

通过下图，首先可以对数据结构和算法有个全面的认识。

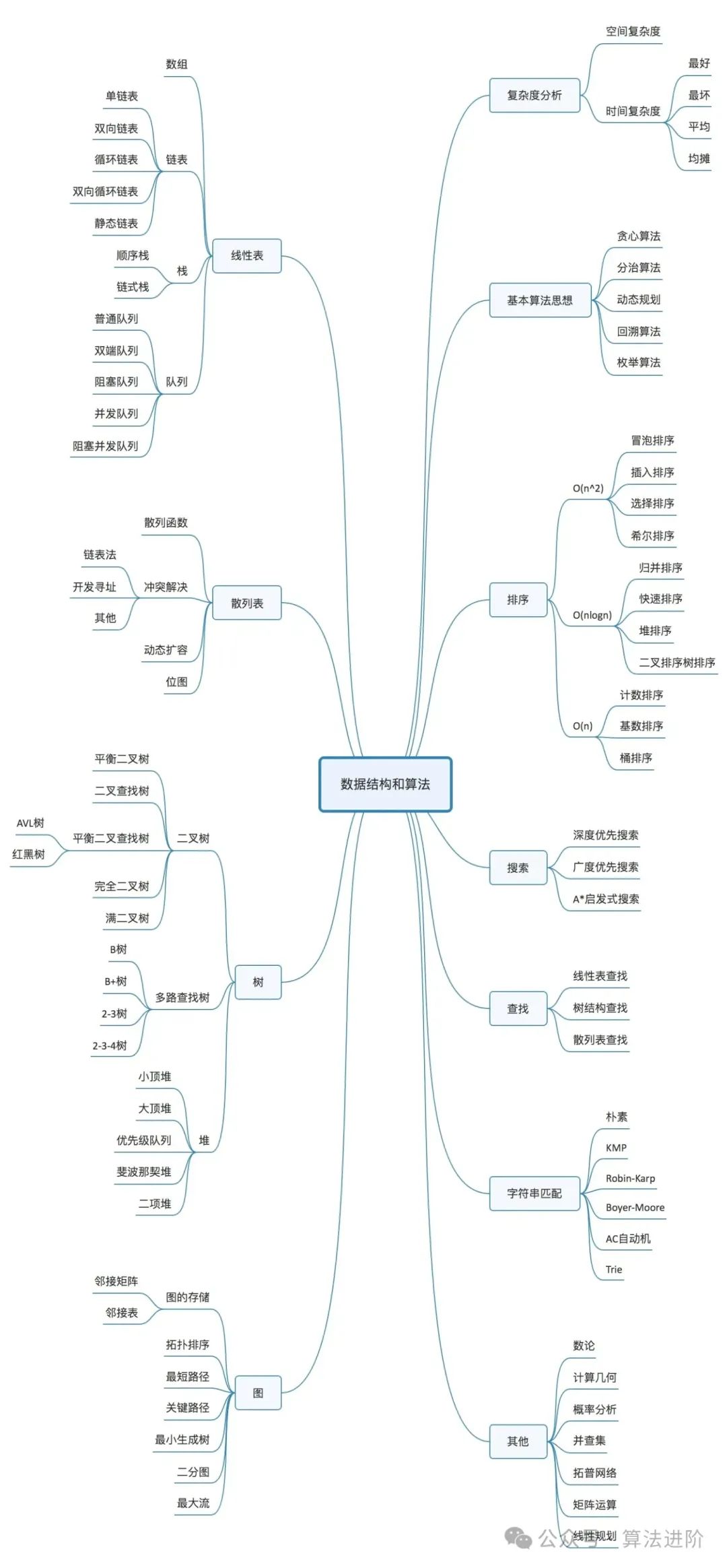
三  数据结构

主要有线性表、树、图等，数据结构的操作主要有：增删改查以及随机访问

3.1 线性表与基础操作

数据结构的核心操作主要包括增删改查及随机访问，其典型代表包括线性表（如数组、链表）、树、图等。

数组

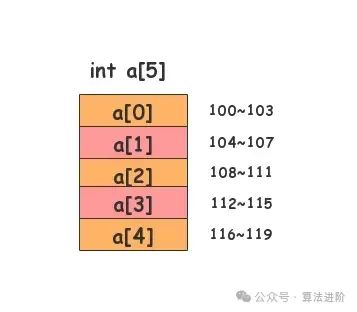
数组是最基础、最简单的数据结构，其特点在于：

• 存储方式：使用一块连续内存空间存储相同类型的数据。

• 优势：支持随机访问，时间复杂度为 (O(1))。

• 劣势：插入和删除操作需要移动大量元素，平均时间复杂度为 (O(n))。

链表

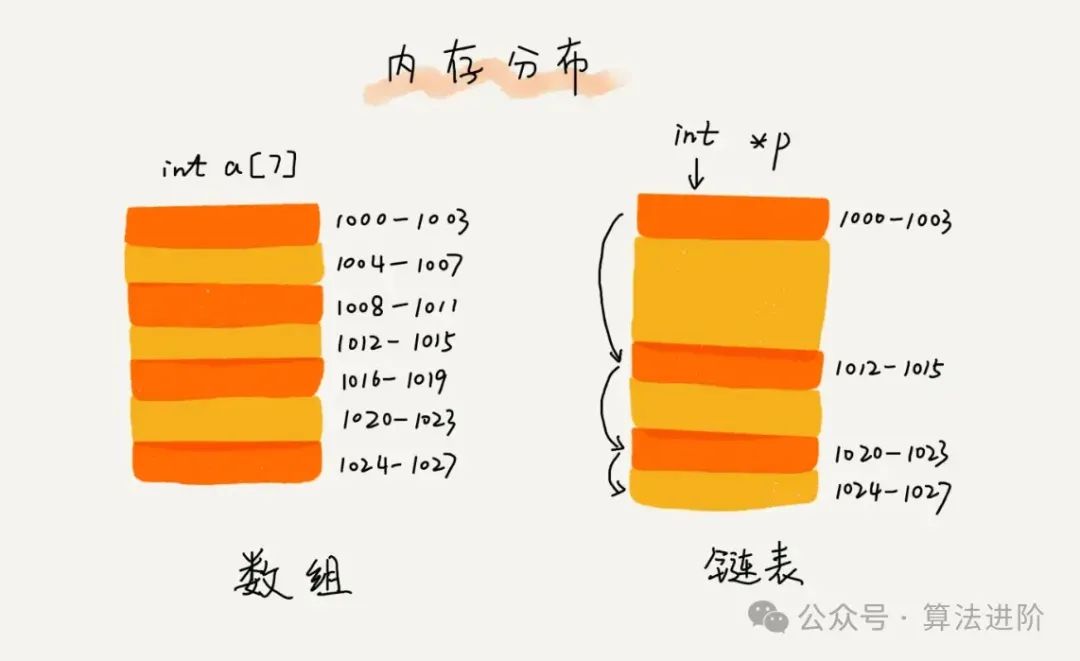
链表通过指针将零散的内存块串联，形成动态数据结构：

• 存储方式：每个节点存储数据及指向下一节点的指针。

• 优势：插入和删除操作高效，时间复杂度为 (O(1))（若已定位节点）。

• 劣势：不支持随机访问，查询时间复杂度为 (O(n))。

数组 vs 链表：

• 数组适合随机访问频繁的场景（如静态数据查询）。

• 链表适合插入、删除频繁的场景（如动态数据操作）。
  实际开发中需根据性能需求综合选择。

栈

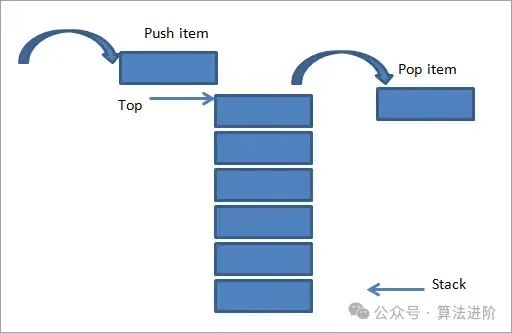
栈是一种操作受限的线性表，遵循后进先出（LIFO）原则：

• 操作：入栈（push）、出栈（pop），时间复杂度均为 (O(1))。

• 应用：浏览器前进/后退功能、函数调用栈等。

队列

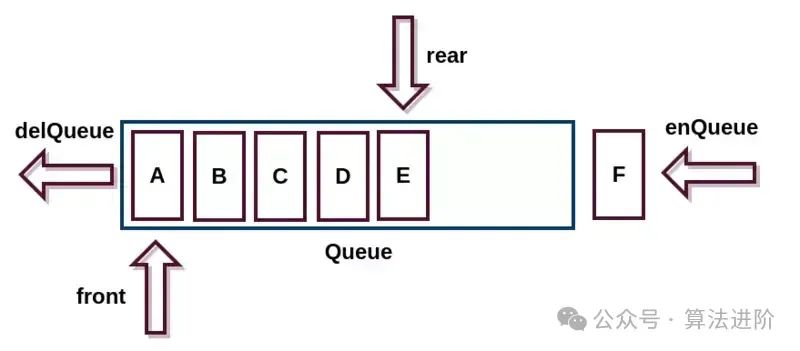
队列是另一种操作受限的线性表，遵循先进先出（FIFO）原则：

• 操作：入队（enqueue）、出队（dequeue）。

• 实现方式：

  • 顺序队列：基于数组实现，需处理数据搬移问题。

  • 链式队列：基于链表实现，避免数据搬移。

  • 循环队列：通过环形数组优化空间利用率。

• 应用：资源池管理（如数据库连接池）、任务排队等。

---

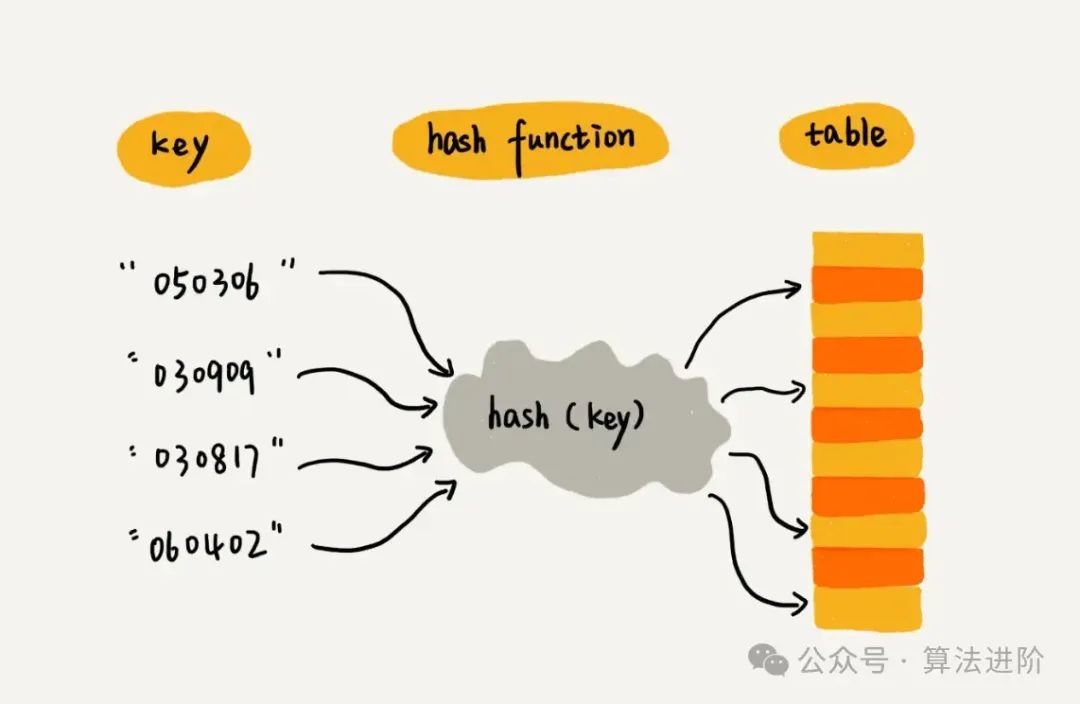
3.2 散列表

散列表（哈希表）是数组的扩展，通过散列函数实现高效的数据存储与查找：

• 核心机制：

  • 时间复杂度在平均情况下，搜索、插入、删除都是O(1)；但在最差情况下，会退化成O(n)。

  • 通过散列函数将键映射为数组下标。

• 关键问题：

  • 散列冲突：常用解决方法包括开放寻址法和链表法。

  • 散列函数设计：直接影响冲突概率与性能。

---

3.3 树结构

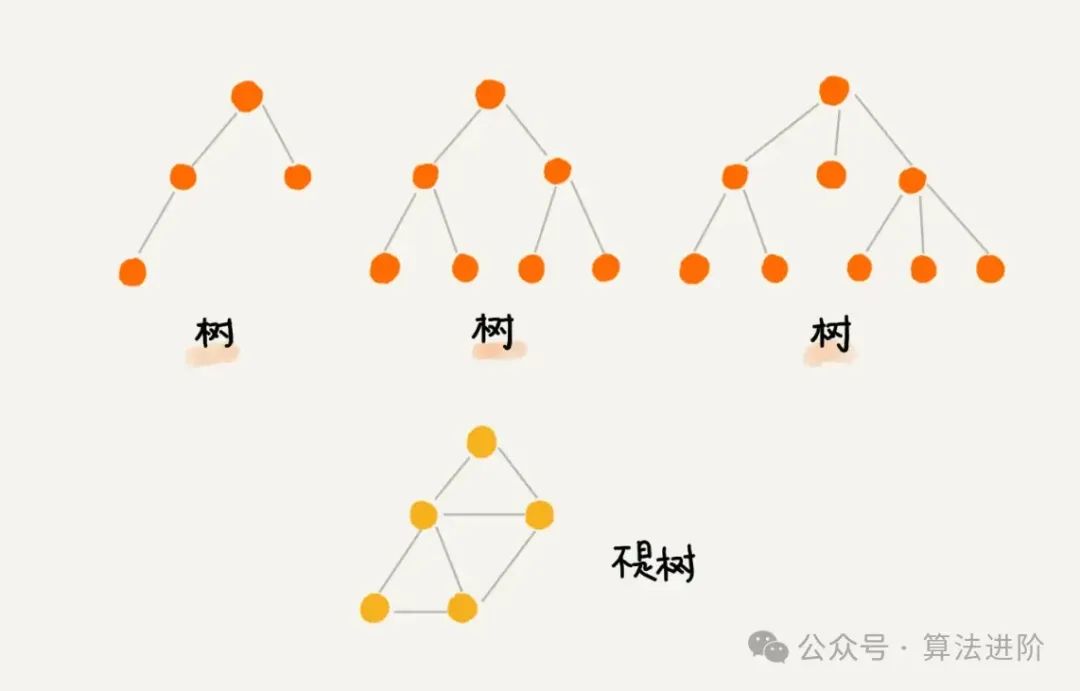
树结构是一种非线性数据结构，每个节点可能有零个或多个子节点。在树结构中，没有父节点的节点称为根节点，而没有子节点的节点称为叶节点。

二叉树

• 定义：每个节点最多有两个子节点（左子节点、右子节点），可为空。

  

• 二叉查找树（BST）：

  • 特性：左子树值 < 根节点值 < 右子树值。

  • 问题：动态更新可能导致树退化（如链表），操作时间复杂度退化为 (O(n))。

平衡二叉树

• 红黑树：通过颜色标记（红/黑）和旋转操作保持近似平衡，高度近似 (\log_2 n)，操作时间复杂度为 (O(\log n))。

Trie 树（前缀树）

• 特性：

  • 专为字符串匹配设计，通过共享前缀节点节省空间。

  • 查找时间复杂度为 (O(k))（(k) 为字符串长度）。

• 应用：

  • 高效解决前缀匹配问题（如搜索引擎关键词提示）。

  • 不适合动态集合查找（可用散列表或红黑树替代）。

B+ 树

• 应用：数据库索引的底层实现。

• 优势：

  • 多叉树结构平衡时间复杂度与空间利用率。

  • 支持高效范围查询与顺序访问。

---

3.4 图结构

图结构通过顶点和边的灵活连接，适用于复杂关系建模（如社交网络、路径规划等）。

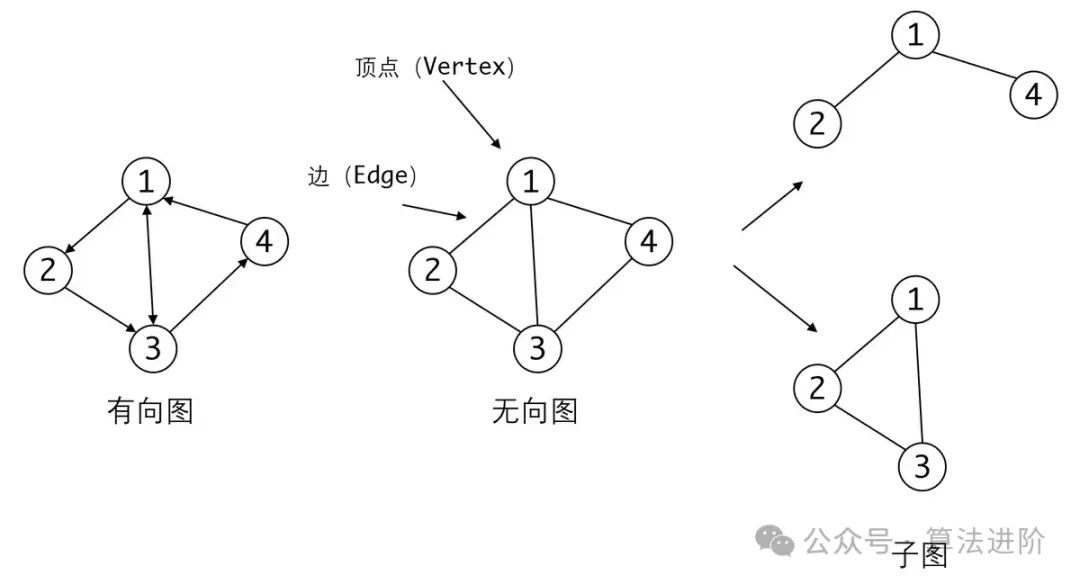
基本概念

• 元素：顶点（Vertex）、边（Edge）。

• 类型：无向图、有向图、带权图。

• 度：

  • 入度（In-degree）：指向某顶点的边数。

  • 出度（Out-degree）：某顶点指出的边数。

存储方式

• 邻接矩阵：

  • 优点：查询效率高，支持矩阵运算。

  • 缺点：空间复杂度为 (O(V^2))（(V) 为顶点数）。

• 邻接表：

  • 优点：空间利用率高，适合稀疏图。

  • 缺点：查询效率低于邻接矩阵。

四 基础算法思想

主要介绍了，归纳、递归、贪心算法、分治算法、回溯算法、动态规划

4.1 Induction（归纳法）

基本思想：
就是初中数学常见的归纳证明题。通过证明基础情况成立，并假设某一步f(1)成立时推导出下一步f(n-1)也成立，从而证明整个命题对所有情况f(n)成立。
实际应用：

• 数学证明（如斐波那契数列通项公式）

• 算法正确性证明（如循环不变式）

代码示例（斐波那契数列通项公式验证）：

ounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(lineounter(linedef fibonacci_inductive(n):    if n <= 1:        return n    a, b = 0, 1    for _ in range(2, n+1):        a, b = b, a + b    return b
# 验证通项公式 F(n) = (φ^n - (1-φ)^n) / √5import mathphi = (1 + math.sqrt(5)) / 2def fibonacci_formula(n):    return round((phi**n - (1-phi)**n) / math.sqrt(5))
# 测试n = 10print(f"迭代法: F({n}) = {fibonacci_inductive(n)}")print(f"通项公式: F({n}) = {fibonacci_formula(n)}")

---

4.2. Reduction（规约）

基本思想：
将复杂问题转化为已知或更易解决的问题，通过解决子问题间接解决原问题。

实际应用：

• NP问题归约（如SAT问题归约到3-SAT）

• 图论问题转化（如最小生成树归约为最短路径）

代码示例（归约子集和问题到0-1背包问题）：

def subset_sum_to_knapsack(nums, target):    # 将子集和问题转化为背包问题    n = len(nums)    dp = [[False] * (target + 1) for _ in range(n + 1)]    dp[0][0] = True    for i in range(1, n + 1):        for w in range(target + 1):            dp[i][w] = dp[i-1][w] or (w >= nums[i-1] and dp[i-1][w-nums[i-1]])    return dp[n][target]
# 测试nums = [3, 34, 4, 12, 5, 2]target = 9print(f"是否存在子集和为{target}: {subset_sum_to_knapsack(nums, target)}")

---

4.3. Recursion（递归）

基本思想：
将问题分解为规模更小的同类子问题，通过递归调用自身解决。
通俗类比：
像俄罗斯套娃，打开外层娃娃后继续打开内层。

实际应用：

• 阶乘计算

• 树的遍历（如前序遍历）

代码示例（递归实现阶乘）：

def factorial(n):    if n == 0:        return 1    return n * factorial(n-1)
print(f"5! = {factorial(5)}")

---

4.4. Divide and Conquer（分治）

基本思想：
将问题分解为独立子问题，递归解决后合并结果。

实际应用：

• 归并排序

• 快排

• 二分查找

代码示例：
快排算法和归并排序很类似的， 都是分治思想，代码上都可以递归实现​​​​​​​

# 快速排序def quick_sort(arr):    if len(arr) <= 1: return arr  # 终止条件    pivot = arr[len(arr)//2]  # 选择基准值  需要注意代码无考虑重复值情况    left = [x for x in arr if x < pivot]  # 规约到更小的子问题    right = [x for x in arr if x > pivot]    return quick_sort(left) + [pivot] + quick_sort(right)  # 合并结果
# 测试：排序 [3,6,8,10,1,2,1]print(quick_sort([1,3,6,8,10,1,1,2,31,33,23,5,2,1]))  

代码示例（二分查找）：​​​​​​​

def binary_search_recursive(arr, target, left, right):    if left > right:        return -1  # 未找到目标值
    mid = (left + right) // 2    if arr[mid] == target:        return mid  # 找到目标值，返回索引    elif arr[mid] < target:        return binary_search_recursive(arr, target, mid + 1, right)  # 搜索右半部分    else:        return binary_search_recursive(arr, target, left, mid - 1)  # 搜索左半部分

---

4.5. 动态规划（Dynamic Programming）

基本思想：
通过存储子问题解避免重复计算，通常用于有重叠子问题和最优子结构的问题。
动态规划（DP）本质上是分治策略的优化版本，两者都遵循"分解→解决→合并"的基本范式，但关键差异在于子问题的重叠性处理。

区别详解

1. 子问题性质

   • 分治策略：子问题相互独立（如归并排序中左右子数组的排序互不影响）

   • 动态规划：子问题存在重叠（如斐波那契数列中fib(5)需要重复计算fib(3)）

计算方式

分治策略：简单递归导致重复计算

动态规划：存储中间结果​​​​​​​

# 经典分治实现斐波那契（效率低下）def fib(n):    if n <= 1: return n    return fib(n-1) + fib(n-2)  # 存在大量重复计算​​​​

# DP优化版斐波那契（O(n)时间复杂度）def fib_dp(n, memo={}):    if n <= 1: return n    if n not in memo:        memo[n] = fib_dp(n-1) + fib_dp(n-2)  # 计算结果存入字典    return memo[n]

1. ​​​​​​​适用场景
2. • 标准分治：适合子问题无重叠的场景（如二分查找、快速排序）

   • 动态规划：适合具有以下特征的问题：

     • 最优子结构（全局最优包含局部最优）

     • 重叠子问题

     • 无后效性（当前决策不影响之前状态）

---

4.6. 贪心算法（Greedy）

基本思想：
每一步选择当前最优解，期望通过局部最优达到全局最优。机器学习的梯度优化也是这个思想。

实际应用：

• 活动选择问题

• 哈夫曼编码

代码示例（活动选择问题）：​​​​​​​

def activity_selection(activities):    activities.sort(key=lambda x: x[1])  # 按结束时间排序    selected = [activities[0]]    last_end = activities[0][1]    for start, end in activities[1:]:        if start >= last_end:            selected.append((start, end))            last_end = end    return selected
# 测试activities = [(1, 4), (3, 5), (0, 6), (5, 7), (3, 8), (5, 9)]print(f"最大兼容活动集: {activity_selection(activities)}")

---

4.7. 枚举算法（Enumeration）

基本思想：
就是暴力求解，穷举所有可能解，逐一验证。像试密码，从0000试到9999。

实际应用：

• 百钱买百鸡问题

• 旅行商问题（小规模）

代码示例（百钱买百鸡）：

def hundred_chickens():    solutions = []    for x in range(21):  # 公鸡最多20只        for y in range(34):  # 母鸡最多33只            z = 100 - x - y            if 5*x + 3*y + z/3 == 100:                solutions.append((x, y, z))    return solutions
print(f"百钱买百鸡方案: {hundred_chickens()}")

---

4.8. 回溯算法（Backtracking）

基本思想：
通过递归尝试所有可能路径，发现无效时回溯。
通俗类比：
像走迷宫，遇到死胡同时返回上一步。

实际应用：

• N皇后问题

• 数独求解

代码示例（N皇后问题）：​​​​​​​

def solveNQueens(n):    def backtrack(row, cols, diagonals1, diagonals2):        if row == n:            result.append(["."*i + "Q" + "."*(n-i-1) for i in cols])            return        for col in range(n):            diag1, diag2 = row-col, row+col            if col in cols or diag1 in diagonals1 or diag2 in diagonals2:                continue            cols.add(col)            diagonals1.add(diag1)            diagonals2.add(diag2)            backtrack(row+1, cols, diagonals1, diagonals2)            cols.remove(col)            diagonals1.remove(diag1)            diagonals2.remove(diag2)
    result = []    backtrack(0, set(), set(), set())    return result
# 测试n = 4solutions = solveNQueens(n)print(f"{n}皇后问题共有{len(solutions)}种解法:")for solution in solutions:    for row in solution:        print(row)    print()

---

总结对比

算法	核心思想	适用场景	复杂度示例
归纳法	数学证明	理论验证	-
规约	问题转化	复杂问题简化	-
递归	自调用分解问题	树结构、分治基础	O(2^n)（如斐波那契）
分治	分而治之+合并	排序、FFT	O(n log n)
动态规划	子问题最优解存储	背包、LCS	O(n*W)
贪心	局部最优	活动选择、哈夫曼编码	O(n log n)
枚举	穷举验证	小规模组合问题	O(2^n)
回溯	递归+剪枝	N皇后、数独	O(n!)

文末附上一些宝藏网站，

• 数据结构算法可视化：https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

• 程序员最爱的leetcode ：https://leetcode.cn/     借此聊聊面试技巧，可以有目的性先刷高频面试题，再查缺补漏尝试不同类型题目。 还有，面试过程遇到不会的题目，是可能和面试官商量换一波的。再者，不会的题目也可以试着给出思路，或者给出虽然不是最优解的方法。面试官也是很乐意引导你优化思路的~

  最后，面试很看缘分的，good luck！祝大家都收获满意的offer！

THE END !

文章结束，感谢阅读。您的点赞，收藏，评论是我继续更新的动力。大家有推荐的公众号可以评论区留言，共同学习，一起进步。