PyTorch深度学习实践概论笔记3-梯度下降算法

上一讲PyTorch深度学习实践概论笔记2-线性模型介绍了线性模型的处理过程，还有课后作业解答。

接下来进入《Pytorch深度学习与实践》第3讲：梯度下降算法，是训练模型时常用的算法。

0 Revison

回忆上一讲：构建学习系统，什么样的函数形势对于数据集是最佳的。针对我们数据集，选择了最简化的线性模型y = x*w，然后使用穷举法搜索w，使得损失函数最小。但是如果纬度多起来，这个方法不太可行。那我们可以考虑分治法。分治算法比如要搜索100个点，先把横纵坐标分成4份，先取16个点，看那一个点得到的值最接近真实值，然后在该点所在区域划分区域继续取值。但是对于非凸函数来讲，这样容易错过比较好的解。所以观察法和分治法的缺陷都比较明显，而且对于高纬度的数据集执行起来比较困难。

1 Optimization Problem

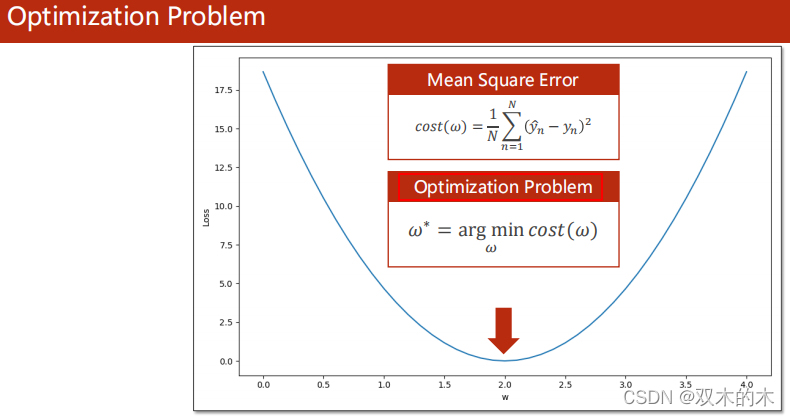
我们把找使目标函数最小的权重组合的任务叫做优化问题。

2 Gradient Descent Algorithm

2.1 理论讲解

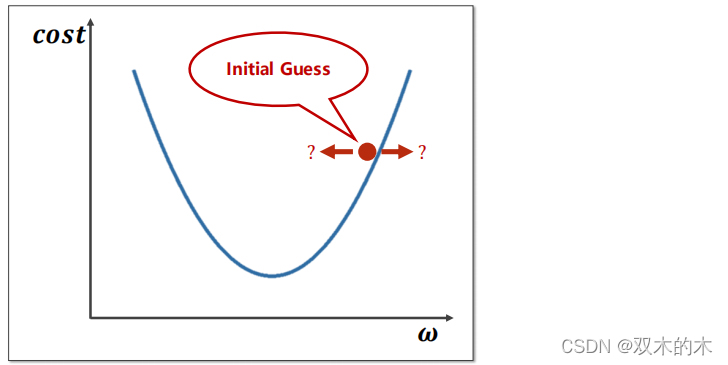
假设初始点w在红色圆点位置，要到达下面的最小值，那么权重w到底往哪个方向走？

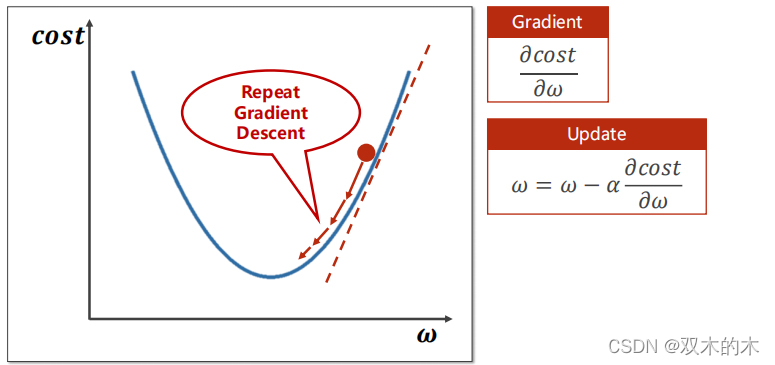
可以根据梯度的定义来决定。

如上图所示，计算梯度，然后乘上学习率update。可以看到每一次迭代都朝着下降最快的方向进行。这其实是一种贪心算法，不一定能得到最优的结果，但是能得到局部区域最优的结果。（具体操作理论看吴恩达老师讲解：1-3 Coursera吴恩达《神经网络与深度学习》第三周课程笔记-浅层神经网络的3.9小节）

那我们为什么还会选择梯度下降法呢？因为深度学习里面的损失函数中并没有非常多的局部最优点，很能陷入局部最优，有一种特殊的点，叫做鞍点（梯度为零，形状像马鞍）。马鞍点推荐学习李宏毅老师讲解：2-2 李宏毅2021春季机器学习教程-类神经网络训练不起来怎么办（一）局部最小值与鞍点。

2.2 Implementation代码讲解

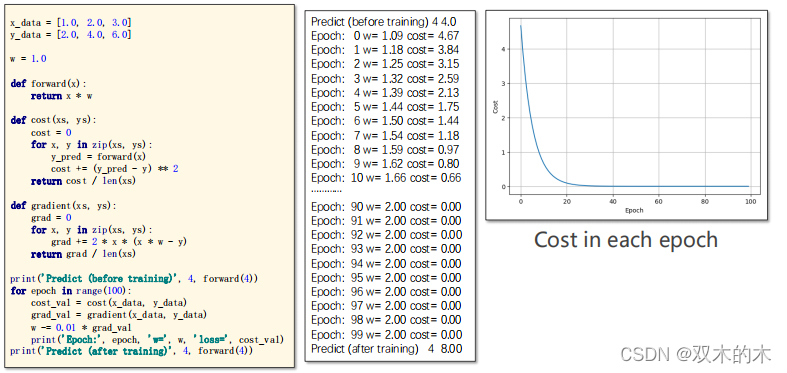
绘制cost和epoch的图像发现，随着迭代的进行，cost越来越小，趋近于0；w越来越趋近于2。而且一开始的时候cost下降很快，越往后下降速度越来越慢，表示训练过程趋近收敛。如果发现Loss为0可以提前结束，但是实际情况不容易出现（数据有噪声），将来会使用加权均值进行loss平滑。如果训练发散（loss函数突然越来越大），可以尝试把学习率调低。

应用中直接使用梯度下降法挺少，而是下面的方法。

#准备训练集
x_data = [1.0, 2.0, 3.0]

y_data = [2.0, 4.0, 6.0]
#初始权重

w = 1.0
#定义模型

def forward(x):

    return x * w
    

#定义损失函数
def cost(xs, ys):

    cost = 0

    for x, y in zip(xs, ys):

    	y_pred = forward(x)

    	cost += (y_pred - y) ** 2

    return cost / len(xs)
    

#定义梯度函数
def gradient(xs, ys):

    grad = 0

    for x, y in zip(xs, ys):

    	grad += 2 * x * (x * w - y)

    return grad / len(xs)


print('Predict (before training)', 4, forward(4))
#update

for epoch in range(100):

    cost_val = cost(x_data, y_data)

    grad_val = gradient(x_data, y_data)

    w -= 0.01 * grad_val

    print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)

print('Predict (after training)', 4, forward(4))

3 Stochastic Gradient Descent

3.1 理论讲解

求梯度的时候不是对所有的cost，而是随机选择一个样本，对一个样本的loss求梯度。

3.2 Implementation of SGD代码讲解

【我的理解】在上述训练这个地方（红框内）老师设置的是遍历所有样本，严谨的一点的话可以加random()函数取随机。

老师解释了随机梯度下降法样本之间不能并行，w是有依赖的，时间复杂度高。因此，我们选择一种折中的方式：取batch，小批量随机下降法（注意：一般Batch指所有样本，严谨一点是mini-batch）。

x_data = [1.0, 2.0, 3.0]

y_data = [2.0, 4.0, 6.0]


w = 1.0


def forward(x):

    return x * w
    

def loss(x, y):

    y_pred = forward(x)

    return (y_pred - y) ** 2
    

def gradient(x, y):

    return 2 * x * (x * w - y)
    

print('Predict (before training)', 4, forward(4))


for epoch in range(100):

    for x, y in zip(x_data, y_data):

    	grad = gradient(x, y)

    	w = w - 0.01 * grad

    	print("\tgrad: ", x, y, grad)

    	l = loss(x, y)

    print("progress:", epoch, "w=", w, "loss=", l)

print('Predict (after training)', 4, forward(4))

我运行的结果：

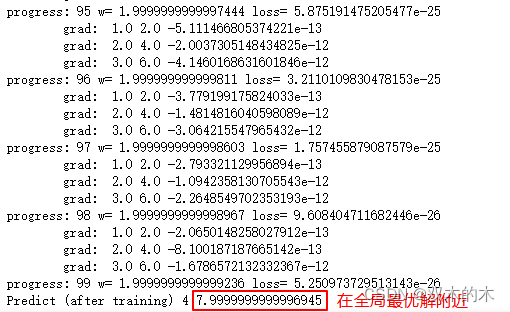
上述结果可以看到：大的整体的方向是向全局最优的，但是最终的结果往往是在全局最优解附近。

说明：记录学习笔记，如果错误欢迎指正！写文章不易，转载请联系我。