蒙特卡罗方法手搓图形

蒙特卡罗方法（Monte Carlo method），又称随机模拟方法，是一种基于概率统计的数值计算方法。下面以绘制一个简单的圆（通过蒙特卡罗方法估算圆的面积进而 “手搓” 出圆的图形示意）为例，使用 Python 语言为你展示如何实现：

import random
import matplotlib.pyplot as plt

# 设定试验次数
n = 10000

# 落在圆内的点的数量
count = 0

# 存储点的坐标
inside_x = []
inside_y = []
outside_x = []
outside_y = []

# 圆的半径
r = 1

for _ in range(n):
    # 生成随机点坐标
    x = random.uniform(-r, r)
    y = random.uniform(-r, r)

    # 判断点是否在圆内
    if x ** 2 + y ** 2 <= r ** 2:
        count += 1
        inside_x.append(x)
        inside_y.append(y)
    else:
        outside_x.append(x)
        outside_y.append(y)

# 估算圆的面积
estimated_area = 4 * count / n

# 绘制点
plt.scatter(inside_x, inside_y, c='blue', label='Inside Circle')
plt.scatter(outside_x, outside_y, c='red', label='Outside Circle')
# 绘制圆
circle = plt.Circle((0, 0), r, fill=False, color='black')
plt.gca().add_artist(circle)

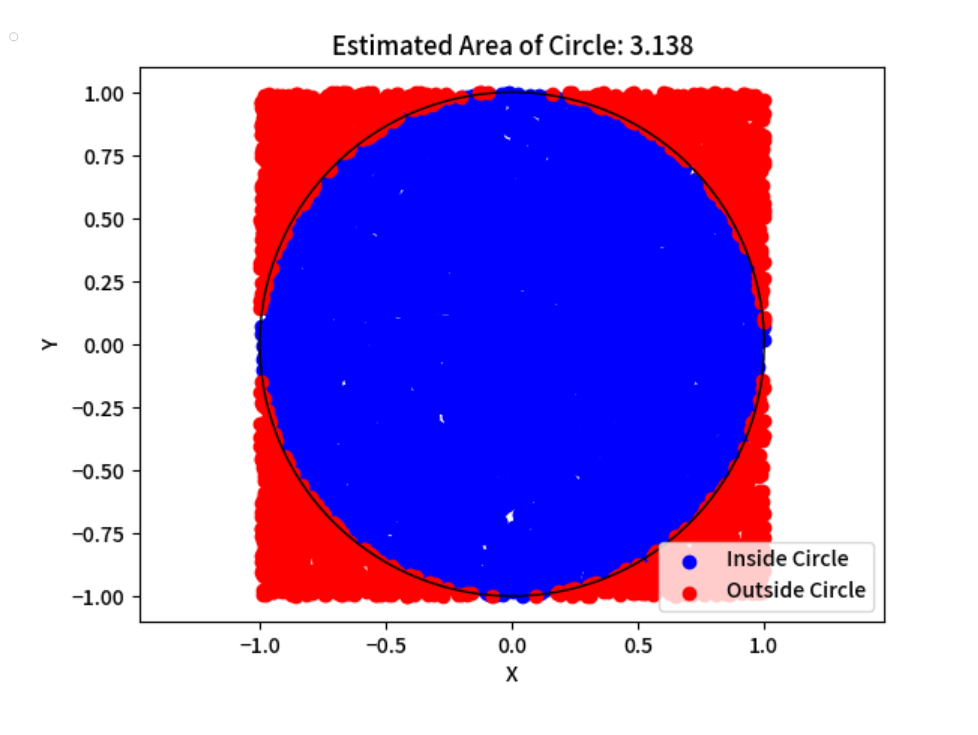
plt.title(f'Estimated Area of Circle: {estimated_area}')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.axis('equal')
plt.show()

上述代码中，我们在一个边长为 2（半径为 1 的圆的外接正方形）的正方形区域内随机生成大量的点，通过判断点是否在圆内（根据点到圆心的距离是否小于等于半径），统计落在圆内的点的数量，进而估算出圆的面积。同时，使用 matplotlib 库将这些点绘制出来，直观地展示出圆的形状以及点的分布情况。