坐标转换（四）——东北天坐标系(ENU)与雷达阵面坐标系(RFC)的相互转换

最新推荐文章于 2025-05-08 19:18:52 发布

小D的线上笔记

最新推荐文章于 2025-05-08 19:18:52 发布

阅读量2.9k

点赞数 30

文章标签：目标跟踪算法

本文链接：https://blog.youkuaiyun.com/crystal__little_girl/article/details/139535406

版权

我们这次要讲的内容是东北天坐标系和雷达阵面坐标系之间的相互转换关系。内容包括东北天坐标系的定义、两种不同的雷达阵面系的定义(第二种定义可能更常见)以及几种坐标系之间的转换。

东北天坐标系和雷达阵面坐标系的直接转换适用于雷达安装于水平、固定的平台上的情况，可用于地基雷达，不适用于雷达安装载体有横滚角或俯仰角变化的情况，如海基雷达(舰载雷达、船载雷达等)、空基雷达(机载雷达、弹载雷达等)、天基雷达(星载雷达等)，如果雷达安装的平台俯仰角或者横滚角是变化的，就需要使用载体坐标系作为中间坐标系进行转换。

1 坐标系的定义

1.1 东北天坐标系

①东北天空间直角坐标系(ENU坐标系)

东北天空间直角坐标系又叫站心坐标、站点坐标系、导航坐标系或者地理坐标系，简称ENU坐标系，E是East的缩写，表示X轴指向的方向为正东；N是North的缩写，表示Y轴指向的方向为正北；U是Up的缩写，表示Z指向的方向为垂直于水平面向上(天顶)，XYZ构成右手坐标系，如图1所示，东北天坐标系我们称为n系。

② 东北天球坐标系(ENU球坐标系)

东北天坐标系对应的球坐标系是以斜距Rng(Range)，方位角Azi(Azimuth)，俯仰角Ele(Elevation)表示的东北天坐标系，下面是它们的定义：

斜距Rng：目标点与东北天球坐标系原点的距离，如图1中的OP，其中O为坐标原点，P为目标点；

方位角Azi：正北方向绕Zn轴顺时针或逆时针旋转到目标点在XOY平面的投影所经过的最小角度，顺时针旋转，方位角为正，逆时针旋转，方位角为负，方位角大小范围为－180°~180°；

俯仰角Ele：原点和目标点的连线与XnOYn平面的夹角，大小范围为-90~90°，俯仰角在XnOYn平面上方(Zn轴正方向)为正，在XnOYn平面下方(Zn轴负方向)为负。

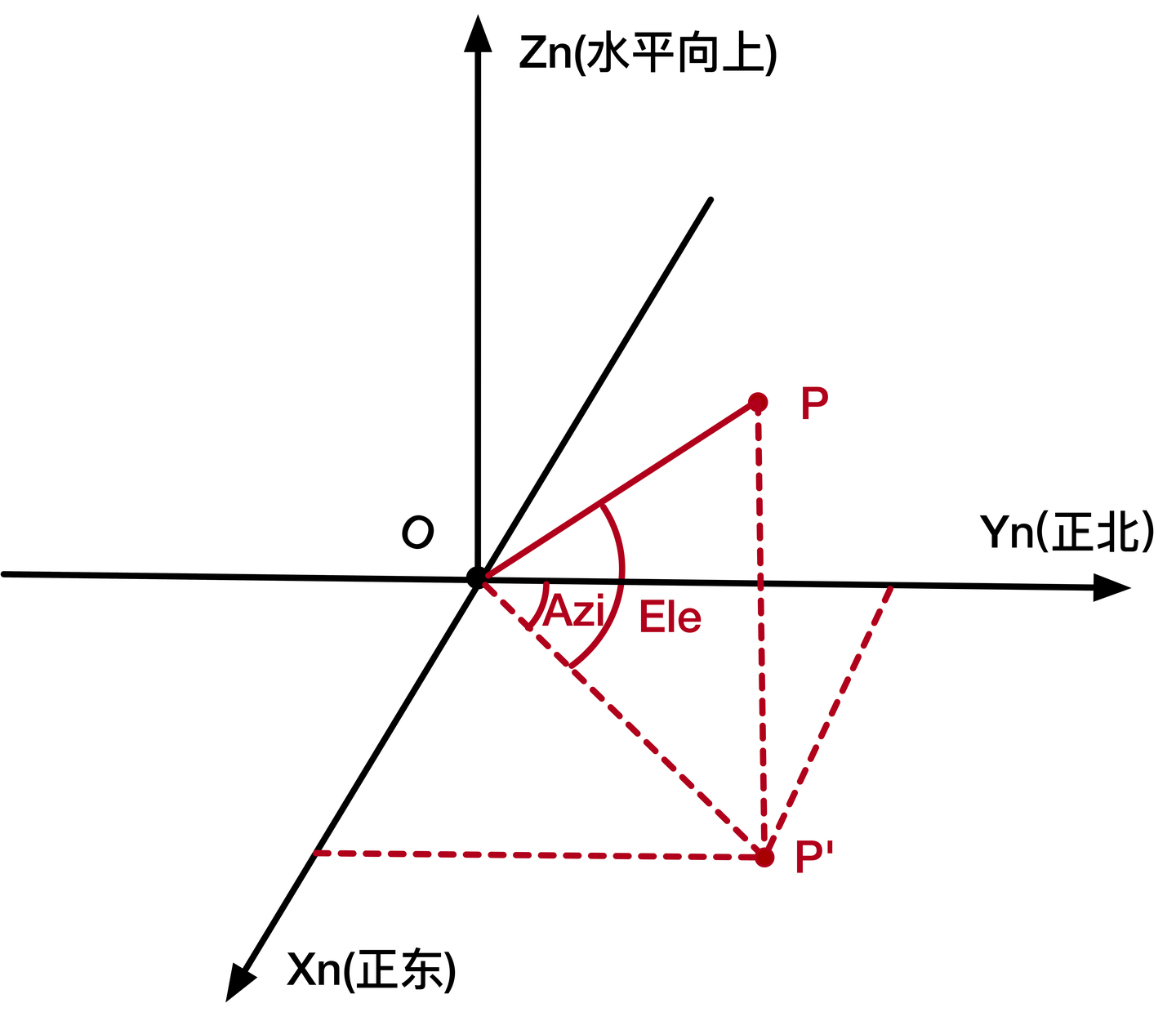
图 1东北天坐标系示意图

1.2 雷达阵面坐标系的第一种定义方式

①雷达阵面空间直角坐标系(RFC坐标系)

雷达阵面空间直角坐标系，即RFC坐标系(Radar Face Coordinates)，它是雷达天线阵面上的坐标系，所以又叫天线坐标系。雷达阵面坐标系称为称为p系，其Xp,Yp,Zp轴有多种定义方式，本文中的雷达阵面空间直角坐标系的第一种定义方式是：Xp轴在阵面内，为当地水平面与阵面的交线；Yp轴也在阵面内，沿着阵面向上；Zp轴为阵面法线，垂直于阵面向上，XpYpZp构成右手坐标系。

图2 RFC坐标系和RFC球坐标系的第一种定义在阵面上的示意图

②雷达阵面球坐标系(RFC球坐标系)

雷达阵面球坐标系是以斜距Rng(Range)，方位角Azi(Azimuth)，俯仰角Ele(Elevation)表示的雷达阵面坐标系，如下图所示。为了便于描述雷达天线波束扫描的方位角和俯仰角，雷达阵面球坐标系和东北天球坐标系中方位角和俯仰角的定义是不一样的。

本文中，雷达阵面球坐标系斜距、方位角和俯仰角的第一种定义如下：

斜距Rng：目标点与原点的距离，如图2中的OP，其中O为坐标原点，P为目标点；

方位角Azi：OZp轴绕Yp轴顺时针或逆时针旋转到目标点在XpOZp平面的投影点与原点O的连线所经过的绝对值最小的角度，从Yp轴正方向往负方向看，OZp轴顺时针旋转方位角为正，逆时针旋转方位角为负。从数学解算角度看，方位角大小范围为-180°~180°，而从目标在阵面前方天线波束才能扫描到目标的角度讲，方位角大小范围为-90°~90°，为了涵盖空间中所有点，本文使用-180°~180°这个范围，当有一个目标点的方位角为-180~-90°或者90~180°这个范围时，这个点可能是无效点，因为雷达看不到阵面背后的目标；

俯仰角Ele：原点与目标点的连线与XpOZp平面的夹角，目标点在XpOZp平面上方(Yp正方向)俯仰角为正，反之为负，俯仰角大小范围为-90°~90°。

注意：根据上面的定义，如果目标点在X轴的正方向，那么目标点的方位角将是负的，这个是没有关系的，上面的定义可以这样理解：假如阵面足够大，你躺在阵面往阵面正前方(Zp正方向)看目标，此时，你的头在沿着阵面向上的方向(Yp正方向)，你的脚在沿着阵面向下的方向(Yp负方向)，如果目标在你的左手边，那么目标阵面方位角为负，如果目标在你的右手边，方位角为正；如果目标在你头的方向，则目标阵面俯仰角为正，目标在你脚的方向，俯仰角为负。口诀是：方位角，左负右正；俯仰角，下负上正。

图3 RCF坐标系与RFC球坐标第一种定义的另一个视角示意图

1.3 雷达阵面坐标系第二种定义方式

雷达阵面坐标系的第二种定义方式用得比较多，这是小D在快写完这篇文章时，在文献中看到的，然后突然明白，原来这种定义才是最常规的定义方式，之前其实也看到过几次，但是由于定势思维的存在，第一次看到的定义在脑子里根深蒂固，就忽略了这种定义。为什么它用得比较多，小D觉得，是因为这样定义旋转起来简单好理解，并且其对应的球坐标系中目标方位角和俯仰角定义和常规的球坐标系中方位角和俯仰角的定义是一致的。

① 雷达阵面空间直角坐标系第二种定义(RFC坐标系)

雷达阵面空间直角坐标系的第二种定义和第一种定义相比，Yp轴和Zp轴交换了下位置，并且Xp的正负方向也做了交换。第二种定义中，Xp轴是阵面与是水平面的交线，Zp轴沿着阵面向上，Yp轴垂直于阵面向上(沿着阵面法线方向)，XpYpZp构成右手坐标系。

图4 RFC坐标系和RFC球坐标系的第二种定义在阵面上的示意图

② 雷达阵面球坐标系第二种定义(RFC球坐标系)

雷达阵面球坐标系的第二种定义方式是常规的球坐标系的定义，与东北天球坐标系的定义是一致的，下面是雷达阵面球坐标系的第二种定义：

斜距Rng：目标点与原点的距离，如下图中的OP；

方位角Azi：Yp轴绕Zp轴旋转到目标点在XpOYp平面的投影所经过的最小角度，范围为-180°~180°，从Zp轴正方向往负方向看，Yp轴顺时针旋转，方位角为正，Yp轴逆时针旋转，方位角为负。

俯仰角Ele：原点与目标点的连线OP与XpOYp平面的夹角，范围为-90°~90°，目标点在Zp轴正方向，俯仰角为正，目标点在Zp轴负方向，俯仰角为负。

图5 RCF坐标系与RFC球坐标第二种定义的另一个视角示意图

2 几种坐标转换

2.1 东北天坐标系(ENU坐标系)与第一种雷达阵面坐标系(RFC坐标系)的相互转换

ENU坐标系与第一种RFC坐标系的转换示意图如下图所示，这个图小D是用OmniGraffle画的，画了很久，主要是第一次用这个软件，不是很熟。有的工具按钮，比如虚线的绘制，自己找了一两个小时才找到；并且这个软件拖动图形的时候，其他图形也会一起跟着动，然后就乱了；到目前为止，小D还没有找到怎么在弧形上加剪头的方法，所以图中表示角度的弧形都没有剪头。总之，还是visio好用一些。

话不多说，我们继续讲东北天坐标系和雷达阵面坐标系的相互转换。

图6 东北天坐标系与第一种雷达阵面坐标系相互转换示意图

图7 图6的侧视图

图8 图6的俯视图

首先，需要介绍一下雷达阵面的安装角，雷达阵面安装角包含两个角度，它们是阵面安装方位角和阵面安装俯仰角，这两个角的定义如下：

阵面安装方位角Ap：正北方向顺时针旋转到阵面法线在水平面的投影所经过的最小角度，范围是0~360°，阵面安装方位角如下图中的Ap所示。

阵面安装俯仰角Ep：阵面法线与水平面的夹角，范围是-90°~90°，阵面安装方位角如上图Ep所示，它同阵面与水平面的夹角是互余的。

① 东北天(ENU)坐标系转换到第一种阵面(RFC)坐标系

东北天坐标系转换到第一种阵面坐标系要经过两个旋转过程，分别是：

a.东北天坐标系O-XnYnZn先绕其Z轴顺时针旋转Ap-180°；

b.旋转后的坐标系再绕其X轴逆时针旋转90°-Ep，形成雷达阵面坐标系O-XpYpZp。

注意：如果阵面安装方位角Ap小于180°，那么Ap-180°就是负的，这个时候，顺时针旋转Ap-180°，相当于逆时针旋转180°-Ap。举个例子，假如Ap=60°，Ap-180°=-120°，按照旋转的第一步，东北天坐标系O-XYZ先绕Z轴顺时针旋转-120°，就相当于绕Z轴逆时针旋转120°。小D之前在这个地方走了点弯路，分成了旋转角度为正和负两种情况来计算旋转矩阵，其实不用分情况。

这样的话，东北天坐标系转换到第一种雷达阵面坐标系的旋转矩阵为：

$\begin{aligned} R^{p}_{n} &= R_{x}\left(\frac{\pi}{2}-E_{p}\right)R_{z}(\pi-A_{p}) \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\left(\frac{\pi}{2}-E_{p}\right) & \sin\left(\frac{\pi}{2}-E_{p}\right) \\ 0 & -\sin\left(\frac{\pi}{2}-E_{p}\right) & \cos\left(\frac{\pi}{2}-E_{p}\right) \end{bmatrix} \begin{bmatrix} \cos(\pi-A_{p}) & \sin(\pi-A_{p}) & 0 \\ -\sin(\pi-A_{p}) & \cos(\pi-A_{p}) & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ &= \left[\begin{matrix} 1 & 0 & 0 \\ 0 & \sin E_{p} & \cos E_{p} \\ 0 & -\cos E_{p} & \sin E_{p} \end{matrix}\right] \left[\begin{matrix} -\cos A_{p} & \sin A_{p} & 0 \\ -\sin A_{p} & -\cos A_{p} & 0 \\ 0 & 0 & 1 \end{matrix}\right] \\ &= \begin{bmatrix} -\cos A_{p} & \sin A_{p} & 0 \\ -\sin E_{p}\sin A_{p} & -\sin E_{p}\cos A_{p} & \cos E_{p} \\ \cos E_{p}\sin A_{p} & \cos E_{p}\cos A_{p} & \sin E_{p} \end{bmatrix} \end{aligned}$

②阵面(RFC)坐标系转换到东北天(ENU)坐标系

阵面坐标系转换到东北天坐标系与东北天坐标系转换到阵面坐标系是一个互逆的过程。所以，计算阵面坐标系转到东北天坐标系的旋转矩阵有两种方法：

方法1：对东北天坐标系转换到第一种阵面坐标系的旋转矩阵求逆或者求转置。

方法2：通过旋转过程计算旋转矩阵。

旋转过程如下：

a.阵面坐标系O-XpYpZp先绕其X轴顺时针旋转90°-Ep；

b.旋转后的坐标系再绕其Z轴逆时针旋转Ap-180°，形成东北天坐标系O-XYZ。

其旋转矩阵计算过程如下：

$\begin{aligned} R^{n}_{p}& =R_{z}(A_{p}-\pi)R_{x}(E_{p}-\frac{\pi}{2}) \\ &=\begin{bmatrix}\cos(A_{p}-\pi)&\sin(A_{p}-\pi)&0\\-\sin(A_{p}-\pi)&\cos(A_{p}-\pi)&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&0&0\\0&\cos(E_{p}-\frac{\pi}{2})&\sin(E_{p}-\frac{\pi}{2})\\0&-\sin(E_{p}-\frac{\pi}{2})&\cos(E_{p}-\frac{\pi}{2})\end{bmatrix} \\ &=\begin{bmatrix}-\cos Ap&-\sin Ap&0\\\sin Ap&-\cos Ap&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&0&0\\0&\sin Ep&-\cos Ep\\0&\cos Ep&\sin Ep\end{bmatrix} \\ &=\begin{bmatrix}-\cos A_{p}&-\sin A_{p}\sin E_{p}&\sin A_{p}\cos E_{p}\\\sin A_{p}&-\cos A_{p}\sin E_{p}&\cos A_{p}\cos E_{p}\\0&\cos E_{p}&\sin E_{p}\end{bmatrix} \end{aligned}\\$

2.2 东北天坐标系(ENU坐标系)与第二种雷达阵面坐标系(RFC坐标系)的相互转换

图9 东北天坐标系与第二种雷达阵面坐标系相互转换示意图

图10 图9的侧视图

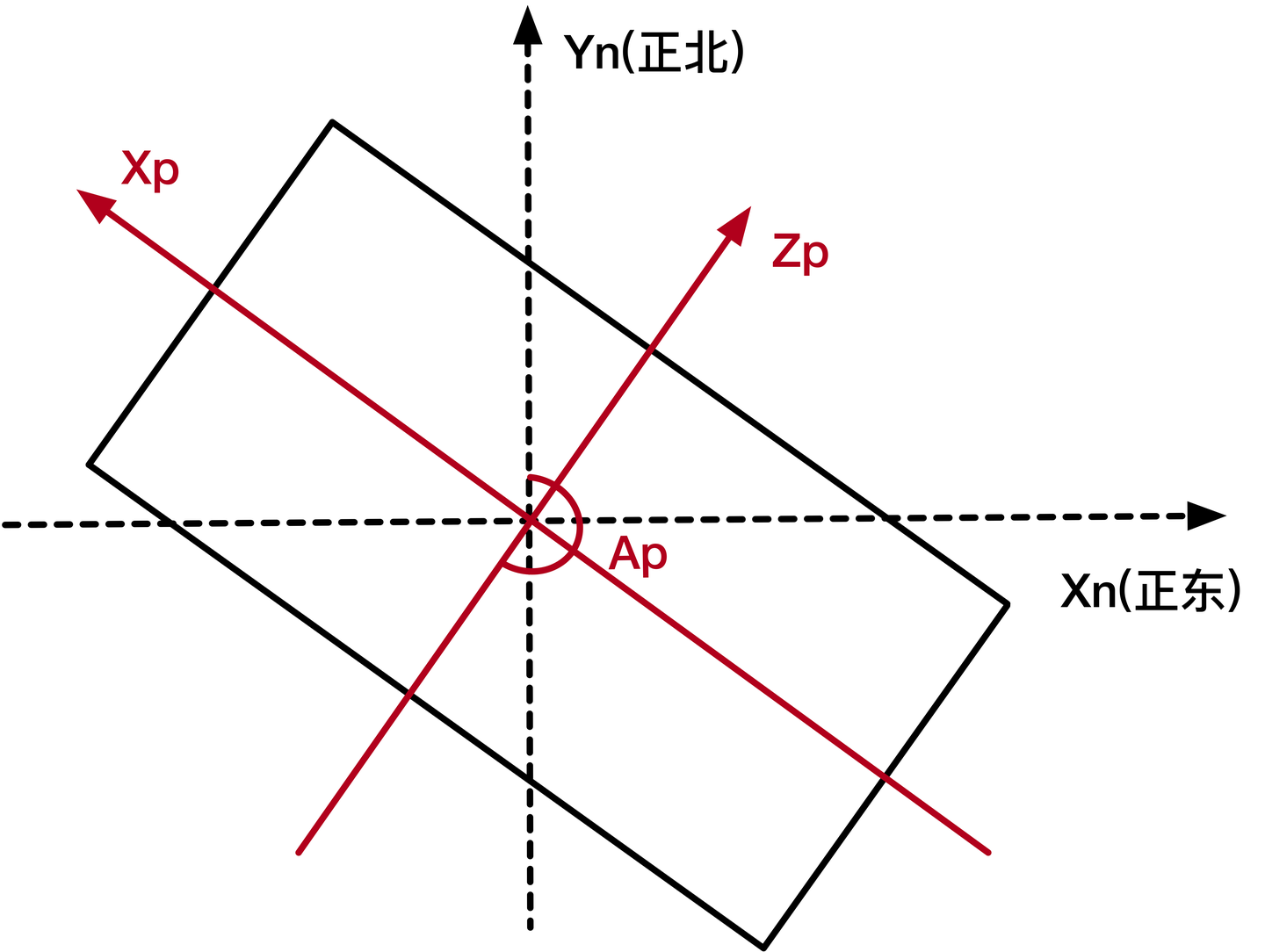
图11 图9的俯视图

①东北天坐标系转到第二种阵面坐标系

首先介绍阵面安装角，雷达安装方位角Ap和雷达安装俯仰角Ep和前文的定义一样，即：

阵面安装方位角Ap：正北方向顺时针旋转到阵面法线在水平面的投影所经过的最小角度，范围是0~360°，阵面安装方位角如下图中的Ap所示。

阵面安装俯仰角Ep：阵面法线与水平面的夹角，范围是-90°~90°，阵面安装方位角如下图Ep所示，它同阵面与水平面的夹角是互余的。

东北天坐标系转换到第二种阵面坐标系的过程为：

a.东北天坐标系O-XnYnZn先绕其Z轴顺时针旋转Ap；

b.旋转后的坐标系再绕其X轴逆时针旋转Ep，得到第二种阵面坐标系O-XpYpZp。

整个过程的旋转矩阵为:

$\begin{aligned}\text{R}^{p}_{n}&=R_x(E_{p})R_{z}(-A_{p})\\&=\begin{bmatrix}1&0&0\\0&\cos E_{p}&\sin E_{p}\\0&-\sin E_{p}&\cos E_{p}\end{bmatrix}\begin{bmatrix}\cos(-A_{p})&\sin(-A_{p})&0\\-\sin(-A_{p})&\cos(-A_{p})&0\\0&0&1\end{bmatrix}\\&=\begin{bmatrix}1&0&0\\0&\cos E_{p}&\sin E_{p}\\0&-\sin E_{p}&\cos E_{p}\end{bmatrix}\begin{bmatrix}\cos A_{p}&-\sin A_{p}&0\\\sin A_{p}&\cos A_{p}&0\\0&0&1\end{bmatrix}\\&=\begin{bmatrix}\cos A_{p}&-\sin A_{p}&0\\\cos E_{p}\sin A_{p}&\cos E_{p}\cos A_{p}&\sin E_{p}\\-\sin E_{p}\sin A_{p}&-\sin E_{p}\cos A_{p}&\cos E_{p}\end{bmatrix}\end{aligned}\\$

②第二种雷达阵面坐标系转换到东北天坐标系

第二种雷达阵面坐标系转到东北天坐标系与东北天坐标系转到第二种雷达阵面坐标系是互逆的过程，这里的互逆是指：旋转顺序相反，并且绕同一个轴旋转的方向相反。比如，A坐标系转换到B坐标系是先绕X轴顺时针旋转α，再绕Y轴逆时针旋转β，那么B坐标系转换到A坐标系就是先绕Y轴顺时针旋转β，再绕X轴逆时针旋转α。

所以，第二种雷达阵面坐标系转换到东北天坐标系的过程有两种方法：

方法1：对东北天坐标系转换到第二种阵面坐标系的旋转矩阵求逆或者求转置。

方法2：根据旋转过程计算旋转矩阵。

第二种雷达阵面坐标系转换到东北天坐标系的旋转过程为：

a.雷达阵面坐标系O-XpYpZp先绕其X轴顺时针旋转Ep；

b.旋转后的坐标系再绕其Z轴逆时针旋转Ap，形成东北天坐标系O-XnYnZn。

其旋转矩阵计算过程为：

$\begin{aligned} R^{n}_{p}& =R_{z}(A_{p})R_{x}(-E_{p}) \\ &=\begin{bmatrix}\cos Ap&\sin Ap&0\\-\sin Ap&\cos Ap&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&0&0\\0&\cos(-Ep)&\sin(-Ep)\\0&-\sin(-Ep)&\cos(-Ep)\end{bmatrix} \\ &=\begin{bmatrix}\cos Ap&\sin Ap&0\\-\sin Ap&\cos Ap&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&0&0\\0&\cos Ep&-\sin Ep\\0&\sin Ep&\cos Ep\end{bmatrix} \\ &=\begin{bmatrix}\cos Ap&0&-\sin Ap\sin Ep\\-\sin Ap&\sin Ap\cos Ep&-\cos Ap\sin Ep\\0&\sin Ep&\cos Ep\end{bmatrix} \end{aligned}\\$