杨辉三角 c++

第一种输出图形（直角三角形）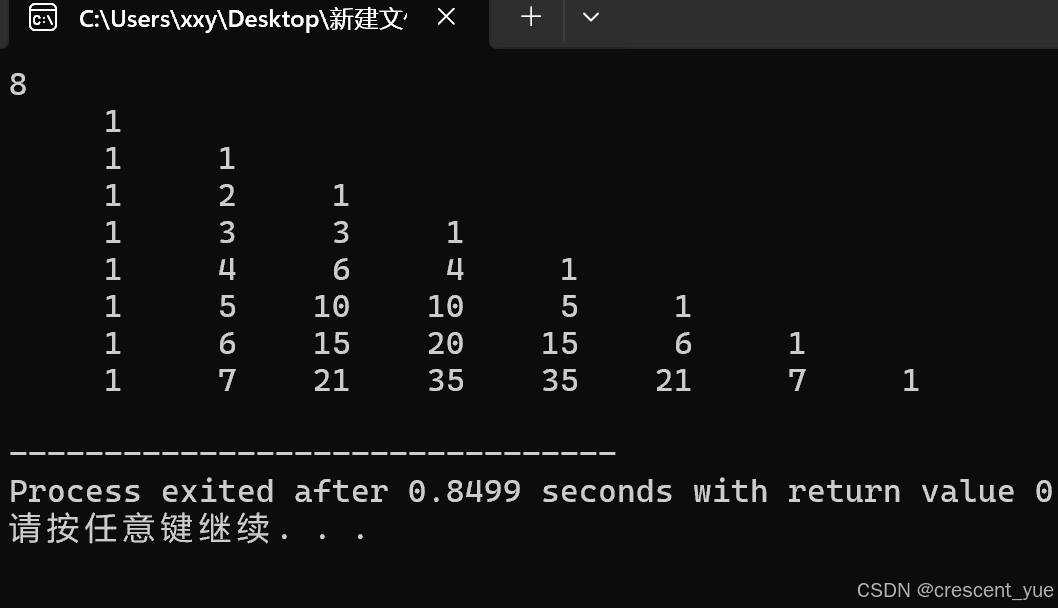 

#include <cstdio>
#include <iostream>
using namespace std;
void yh(int a[10][10],int n){  //定义n<10
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i==j||j==1){    //杨辉三角每行首尾都为1
				a[i][j]=1;
			}
			else a[i][j]=a[i-1][j-1]+a[i-1][j];//上一行数与上一行前一位数之和
		}
	}
	for(int i=1;i<=n;i++){
	    for(int j=1;j<=n;j++){
	    	if(i>=j)
			printf("%6d",a[i][j]);
		}
	printf("\n");	
}
}
int main(){
	int n,a[10][10];
	cin>>n;
	yh(a,n);
	return 0;
}

第二种输出图形（等腰三角形）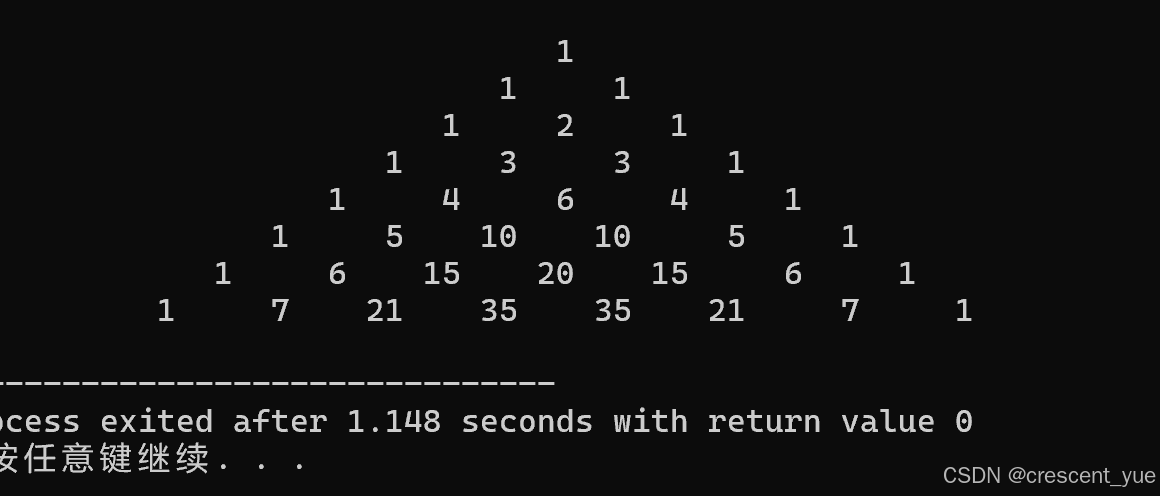 

#include <cstdio>
#include <iostream>
using namespace std;
void yh(int a[10][10],int n){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i==j||j==1){
				a[i][j]=1;
			}
			else a[i][j]=a[i-1][j-1]+a[i-1][j];
		}
	}
	for(int i=1;i<=n;i++){
	    int k=9-i;
        while (k--){
            printf("   ");
        }
	    for(int j=1;j<=n;j++){
	    	if(i>=j)
			printf("%6d",a[i][j]);
		}
	printf("\n");	
}
}
int main(){
	int n,a[10][10];
	cin>>n;
	yh(a,n);
	return 0;
}