超 底层：10WQPS 海量存储HBase/RocksDB，底层 结构是什么？

一次穿透：10WQPS/PB级海量存储HBase/RocksDB的底层LSM结构

LSM tree 是很多数据库内部的核心数据结构，包括BigTable,ClickHouse、Cassandra, Scylla， RocksDB，HBase。

ClickHouse基于Log-Structured Merge-Tree 结构（思想），实现磁盘的顺序写入，和数据的预排序。

Cassandra 是一个使用 LSM 树作为内部数据结构，可以轻松存储万亿级日志，具体请参见：

阿里2面：万亿级消息，如何做存储设计？

RocksDB是 Facebook 开源的一个高性能持久化 KV 存储，越来越多的新生代数据库，都不约而同地选择 RocksDB 作为它们的存储引擎。

前几天时候尼恩辅导一个字节的小伙伴改造简历，得知他们内部使用的可以持久化的自研分布式Redis，就是基于 RocksDB 做的二次架构。

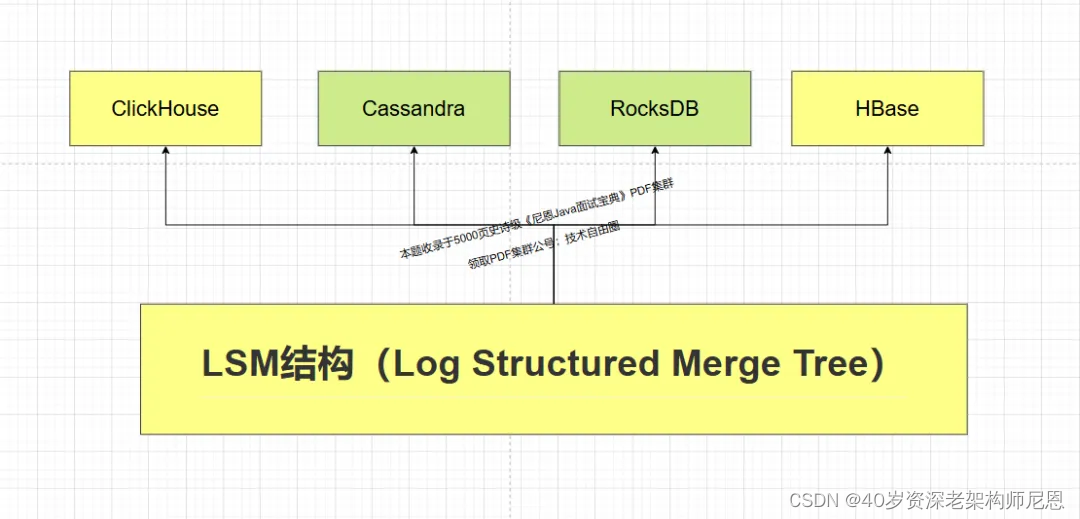
回到工业级的场景：百亿级数据存储架构，只有分库分表吗？

很多的小伙伴来咨询尼恩， 百亿级数据存储怎么架构，说他们的面试中，都遇到的。

他们回到回答了分库分表，比如，当一个表（比如t_order） 达到500万条或2GB时，需要考虑水平分表。

然后面试官，不满意。很多的小伙伴来咨询尼恩，为什么？

这里，尼恩用20年的技术功力，给大家做一个彻底性、系统化梳理，帮助大家吊打面试。

从0到1, 百亿级数据存储架构，怎么设计？

咱们的生产需求上，百亿级数据存储架构， 一般来说，需要具备以下四个能力：

• 高并发的在线ACID事务, 这里需要用到 分库分表

• 高并发的在线搜索, 这里需要用到 ElasticSearch

• 海量数据的离线处理, 这里需要用到 HBase

• 冗余表双写能力 （不同业务维度的副本）

• 把商品数据冗余存储在HBase 中，实现海量数据的离线处理, 同时也具备高速访问的能力

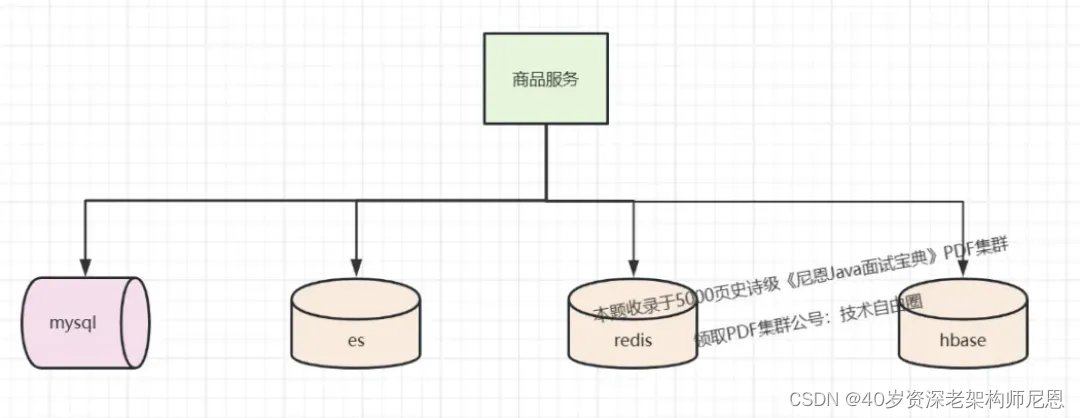
HBase 的底层结构，恰恰是LSM。

所以，咱们必须首先搞定LSM。

LSM结构（Log Structured Merge Tree）的使用场景

log-structured merge-tree (LSM tree) 是一种被精心设计的数据结构，常用于处理大量写入的场景。

通过对写入操作进行顺序写入优化实现性能提升。

Hbase 适合存储 PB 级别的海量数据，在 PB 级别的数据以及采用廉价 PC 存储的情况下，能在几十到百毫秒内返回数据。这与 Hbase 的极易扩展性息息相关。正式因为 Hbase 良好的扩展性，才为海量数据的存储提供了便利。

1. 列式存储

这里的列式存储其实说的是列族存储，Hbase 是根据列族来存储数据的。列族下面可以有非常多的列，列族在创建表的时候就必须指定。

2. 极易扩展

Hbase 的扩展性主要体现在两个方面，一个是基于上层处理能力（RegionServer）的扩展，一个是基于存储的扩展（HDFS）。通过横向添加 RegionSever 的机器，进行水平扩展，提升 Hbase 上层的处理能力，提升 Hbsae 服务更多 Region 的能力。备注：RegionServer 的作用是管理 region、承接业务的访问，这个后面会详细的介绍通过横向添加 Datanode 的机器，进行存储层扩容，提升 Hbase 的数据存储能力和提升后端存储的读写能力。

3. 高并发

由于目前大部分使用 Hbase 的架构，都是采用的廉价 PC，因此单个 IO 的延迟其实并不小，一般在几十到上百 ms 之间。这里说的高并发，主要是在并发的情况下，Hbase 的单个 IO 延迟下降并不多。能获得高并发、低延迟的服务。

4. 稀疏

稀疏主要是针对 Hbase 列的灵活性，在列族中，你可以指定任意多的列，在列数据为空的情况下，是不会占用存储空间的。

LSM结构 简介

全称 Log-Structured Merge-Tree 日志结构合并树，但不是树,它是利用了磁盘顺序读写能力，实现了一个多层的存储结构

1996年，一篇名为 Thelog-structured merge-tree（LSM-tree）的论文创造性地提出了日志结构合并树（ Log-Structured Merge-Tree）的概念，该方法既吸收了日志结构方法的优点，又通过将数据文件预排序克服了日志结构方法随机读性能较差的问题。

尽管当时 LSM-tree新颖且优势鲜明，但它真正声名鹊起却是在 10年之后的 2006年，2006年，Google 发表了 BigTable 的论文。这篇论文提到 BigTable 单机上所使用的数据结构就是 LSM。

那年谷歌的一篇使用了 LSM-tree技术的论文 Bigtable: A Distributed Storage System for Structured Data横空出世，在分布式数据处理领域掀起了一阵旋风，

随后两个声名赫赫的大数据开源组件（ 2007年的 HBase与 2008年的 Cassandra，目前两者同为 Apache顶级项目）直接在其思想基础上破茧而出，彻底改变了大数据基础组件的格局，同时也极大地推广了 LSM-tree技术。

目前，LSM 被很多存储产品作为存储结构，比如 Apache HBase, Apache Cassandra, MongoDB 的 Wired Tiger 存储引擎, LevelDB 存储引擎, RocksDB 存储引擎等。

简单地说，LSM 的设计目标：是提供比传统的 B+ 树更好的写性能。

LSM 通过将磁盘的随机写入转化为顺序写入来提高写性能 ，而付出的代价就是牺牲部分读性能、写放大（B+树同样有写放大的问题）。

LSM-tree最大的特点是同时使用了两部分类树的数据结构来存储数据，并同时提供查询。

其中一部分数据结构（ C0树）存在于内存缓存（通常叫作 memtable）中，负责接受新的数据插入更新以及读请求，并直接在内存中对数据进行排序；

另一部分数据结构（ C1树）存在于硬盘上 (这部分通常叫作 sstable)，它们是由存在于内存缓存中的 C0树冲写到磁盘而成的，主要负责提供读操作，特点是有序且不可被更改。

LSM 相比 B+ 树能提高写性能的本质原因是：

外存——无论磁盘还是 SSD，其随机读写都要慢于顺序读写。

Hash表、二叉树，到B树和B+树 ，LSM树

Hash表和B+树

在了解LSM树之前，我们需要对hash表和B+树有所了解。

hash表通过key值经过hash算法，直接定位到数据存储地址，然后取出value值。

时间复杂度O（1），找数据和存数据就需要那么一下子，就给找到了

hash存储方式支持增、删、改以及随机读取操作，但不支持顺序扫描，对应的存储系统为key-value存储系统。

对于key-value的插入以及查询，哈希表的复杂度都是O(1)，明显比树的操作O(n)快,

如果不需要有序的遍历数据，哈希表就是最佳选择

从二叉树，到B树和B+树的演进

首先从二叉树说起，一颗非常普通的树，非常容易退化为一张链表。

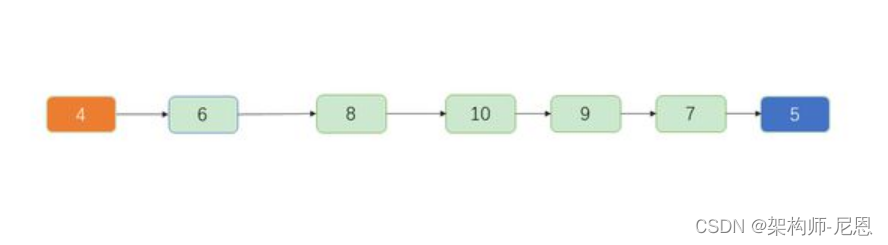
因为 二叉树 会产生退化现象，提出了平衡二叉树，

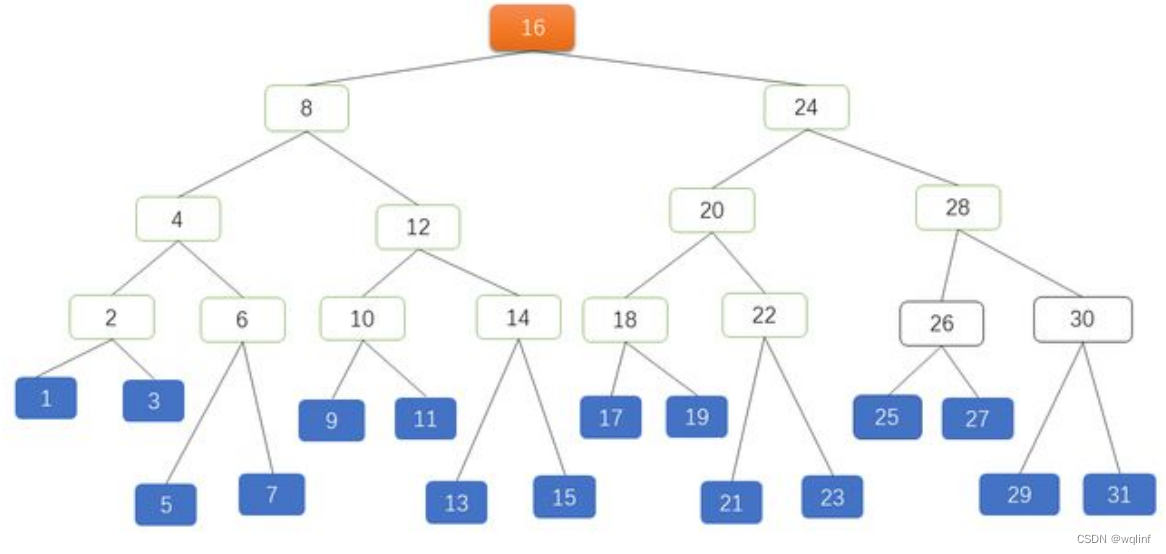
在平衡二叉树基础上， 需要减少遍历高度， 怎样让每一层放的节点多一些数据，来引申出m叉树，

m叉搜索树同样会有退化现象，引出m叉平衡树，也就是B树，

B 树是一种多叉的 AVL 树。B-Tree 减少了 AVL 数的高度，增加了每个节点的 KEY 数量。

B树的问题： 每个节点既放了key也放了value，怎样使每个节点放尽可能多的key值，以减少遍历高度呢（访问磁盘次数），

可以将每个节点只放key值，将value值放在叶子结点，在叶子结点的value值增加指向相邻节点指针，这就是优化后的B+树。

B+树所有叶子节点形成有序链表，便于范围查询，不用每次要检索树。

目前数据库多采用两级索引的B+树，树的层次最多三层，

因此可能需要5次磁盘访问才能更新一条记录（三次磁盘访问获得数据索引以及行id，然后再进行一次数据文件读操作及一次数据文件写操作）

B~树(平衡多路二叉树)

B_{树，又叫平衡多路查找树。一棵m阶的B}树 (m叉树)的特性如下：

1. 树中每个结点至多有m个孩子；

2. 除根结点和叶子结点外，其它每个结点至少有[m/2]个孩子；

3. 若根结点不是叶子结点，则至少有2个孩子；

4. 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；

5. 每个非终端结点中包含有n个关键字信息： (n，A0，K1，A1，K2，A2，…，Kn，An)。

其中，

• a) Ki (i=1…n)为关键字，且关键字按顺序排序Ki < K(i-1)。
• b) Ai为指向子树根的接点，且指针A(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。
• c) 关键字的个数n必须满足： [m/2]-1 <= n <= m-1

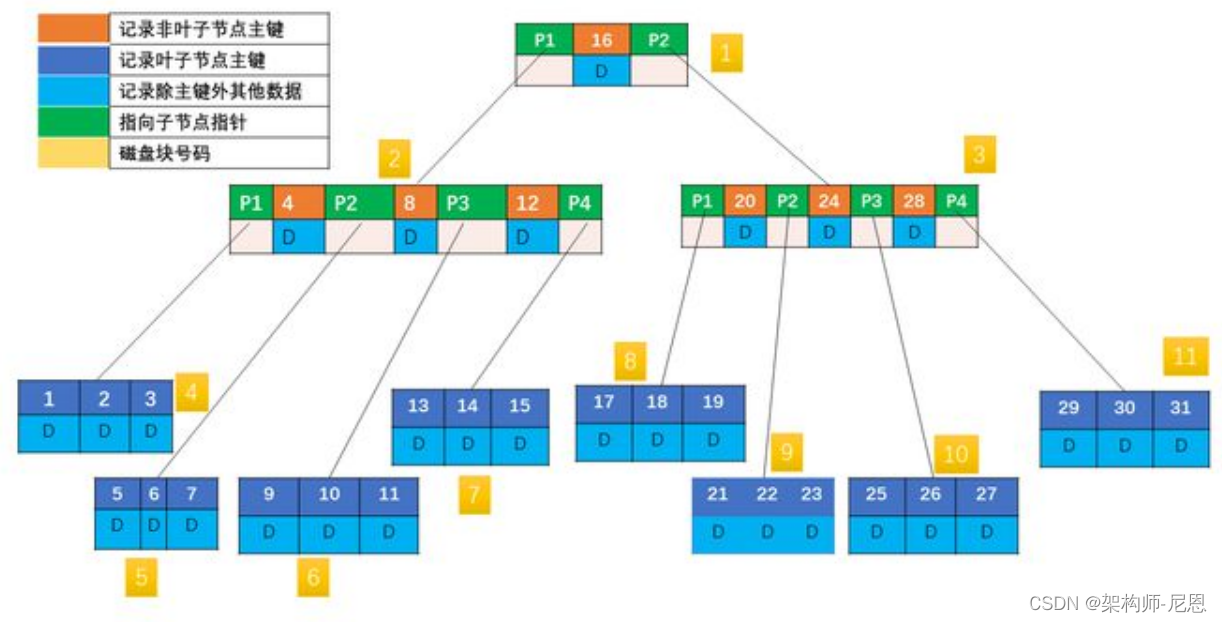
实际应用中，每个节点的最小单元不是 KEY，而一般是按照块（BLOCK）来算。

比如磁盘文件系统 EXT4 每块 4KB；数据库比如 PostgreSQL 是 8KB，MySQL InnoDB 是 16KB， MySQL NDB 是 32KB 等。

上图每个节点的基本单元是一个磁盘块（BLOCK，默认 4KB），根节点含有一个键值，其他节点含有 3 个键值，每个磁盘块包含对应的键值与数据。

比如现在要读取 KEY 为 31 的记录：先找到根节点磁盘块（1），读入内存。（第一次 IO）；

关键字 31 大于区间（16，），根据指针 P2 找到磁盘块 3，读入内存（第二次 IO）；

31 大于区间（20，24，28），根据指针 P4 读取磁盘块 11（第三次 IO），在磁盘块 11 中找到 KEY 为 31 的记录，返回结果。

三次 IO，前两次 IO 其实从磁盘读取了不必要的数据，因为只用比较 KEY，所以非叶子节点对应的 DATA 完全没有必要，如果 DATA 很大，那完全是浪费内存资源。

考虑下能否把非叶子节点的 DATA 拿掉？

B+树

B+树：是应文件系统所需而产生的一种B~树的变形树。

一棵m阶的B+树和m阶的B-树的差异在于：

1. 有n棵子树的结点中含有n个关键字； (B~树是n棵子树有n+1个关键字)

2. 所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (B~树的叶子节点并没有包括全部需要查找的信息)

3. 所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (B~树的非终节点也包含需要查找的有效信息)

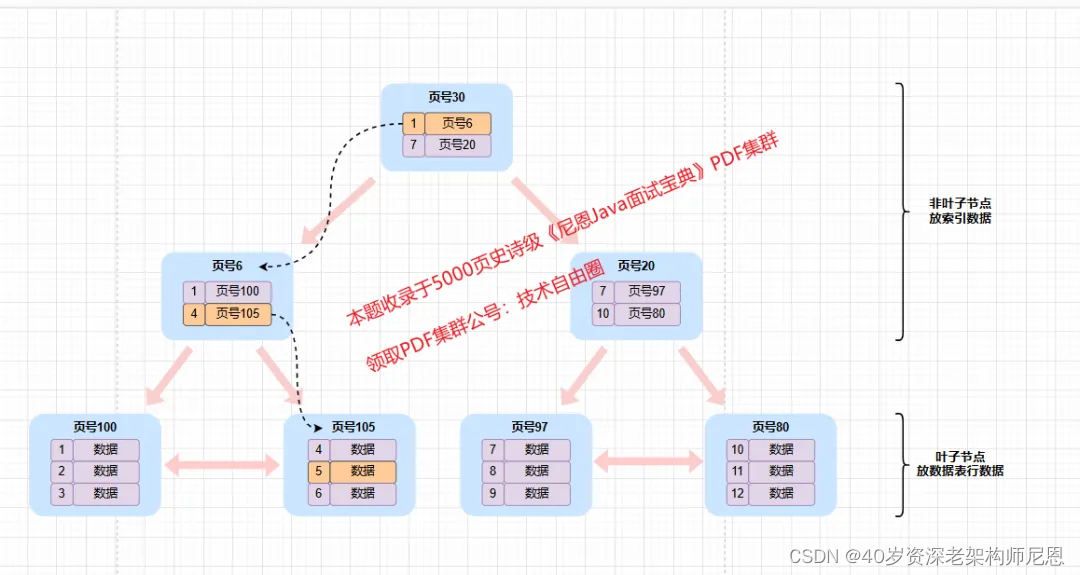
非叶子节点不再包含除了主键外的数据，数据全部放在叶子节点，并且所有叶子节点存放在一个单向链表里，当然也可以双向链表。

可以看到，B+ 树同时具有平衡多叉树和链表的优点，即可兼顾 B 树对范围查找的高效，又可兼顾链表随机写入的高效， 这也是大部分数据库都用 B+ 树来存储索引的原因。

（1）B+树的磁盘读写代价更低
我们都知道磁盘时可以块存储的，也就是同一个磁道上同一盘块中的所有数据都可以一次全部读取。

而B+树的内部结点并没有指向关键字具体信息的指针

比如文件内容的具体地址 ， 比如说不包含B~树结点中的FileHardAddress[filenum]部分 。

因此其内部结点相对B~树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。

这样，一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。

举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。

一棵9阶B~树(一个结点最多8个关键字)的内部结点需要2个盘快。而B+树内部结点只需要1个盘快。

当需要把内部结点读入内存中的时候，B~树就比B+数多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

（2）B+树的查询效率更加稳定。

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。

所以任何关键字的查找必须走一条从根结点到叶子结点的路。

所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

B-tree和B+树的区别：

比较项	B树	B+树
指针	所有内部和叶节点都有数据指针	只有叶节点有数据指针
搜索	由于并非所有键都在叶中可用，因此搜索通常需要更多时间。	所有的键都在叶节点，因此搜索更快更准确。
冗余键	树中没有保留键的副本。	保留密钥的副本，并且所有节点都存在于叶子中。
插入	插入需要更多时间，而且有时无法预测。	插入更容易，结果始终相同。
删除	内部节点的删除非常复杂，树必须经历很多变换。	删除任何节点都很容易，因为所有节点都在叶子上找到。
叶节点	叶节点不存储为结构链表。	叶节点存储为结构链表。
使用权	无法顺序访问节点	可以像链表一样顺序访问
高度	对于特定数量的节点高度较大	对于相同数量的节点，高度小于 B 树
应用	用于数据库、搜索引擎的 B 树	B+ 树用于多级索引、数据库索引
节点数	任何中间层 ‘l’ 的节点数是 2 l。	每个中间节点可以有 n/2 到 n 个子节点。

B+树的不足，与LSM树诞生背景

传统关系型数据库使用btree或一些变体作为存储结构，能高效进行查找。

但保存在磁盘中时它也有一个明显的缺陷，那就是逻辑上相离很近但物理却可能相隔很远，这就可能造成大量的磁盘随机读写。

随机读写比顺序读写慢很多，为了提升IO性能，我们需要一种能将随机操作变为顺序操作的机制，于是便有了LSM树。

为啥 随机读写比顺序读写慢很多呢？

磁盘读写时涉及到磁盘上数据查找，地址一般由柱面号、盘面号和块号三者构成。

也就是说：

step1：移动臂先根据柱面号移动到指定柱面，

step2： 然后根据 盘面号 确定盘面

step3：最后 块号 确定磁道，最后将指定的磁道段移动到磁头下，便可开始读写。

整个过程主要有三部分时间消耗，查找时间(seek time) +等待时间(latency time)+传输时间(transmission time) 。分别表示定位柱面的耗时、将块号指定 磁道段 移到磁头的耗时、将数据传到内存的耗时。

整个磁盘IO最耗时的地方在查找时间，所以减少查找时间能大幅提升性能。

基于 B+ 树的 传统存储引擎，是为旋转磁盘设计的，写入速度很慢，并且只提供基于块的寻址。

B+ 树的 传统存储引擎，是为旋转磁盘设计的

磁盘读写时涉及到磁盘上数据查找，地址一般由柱面号、盘面号和块号三者构成。

也就是说移动臂先根据柱面号移动到指定柱面，然后根据盘面号确定盘面的磁道，最后根据块号将指定的磁道段移动到磁头下，便可开始读写。

整个过程主要有三部分时间消耗，查找时间(seek time) +等待时间(latency time)+传输时间(transmission time) 。分别表示定位柱面的耗时、将块号指定磁道段移到磁头的耗时、将数据传到内存的耗时。

整个磁盘IO最耗时的地方在查找时间，所以减少查找时间能大幅提升性能。

关于磁盘IO这一部分，其实要区别看待。

如果采用的是ssd，那么对于任意地址而言，其实寻址时间可以认为是固定的，它与最传统的chs以及lba寻址方式不一样。如果是ssd的话，随机读写和顺序读写，开销差距大吗？

HDD机械硬盘的扇区（sector）结构

机械硬盘的性能为啥那么慢？ 看看结构就知道：

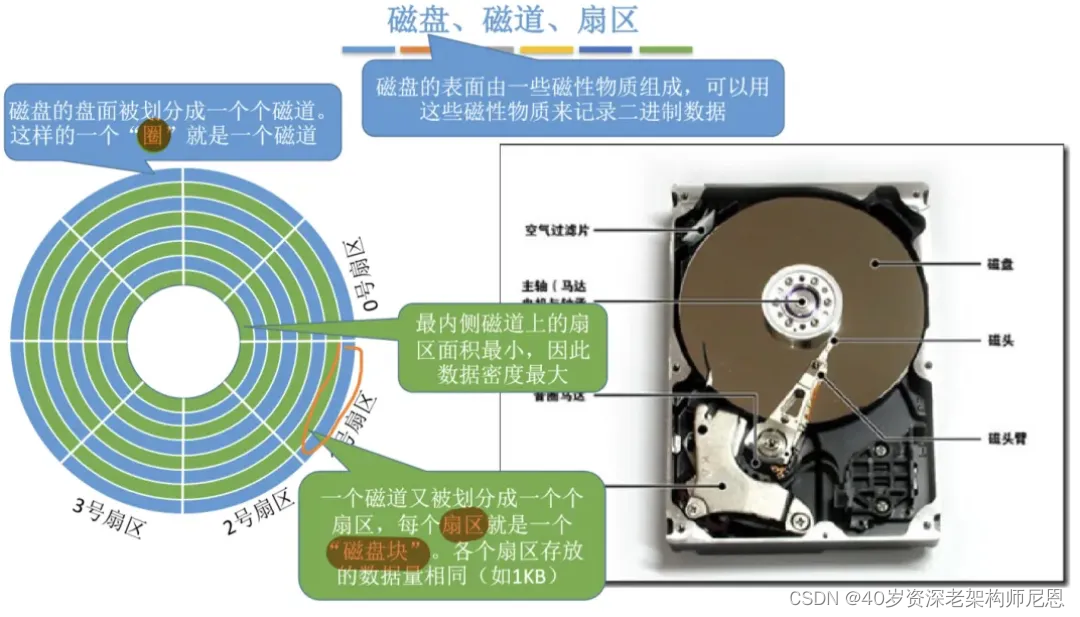
机械磁盘上的每个磁道被等分为若干个弧段，这些弧段称之为扇区。

如何在磁盘中读/写数据？ 需要 物理动作，去移动 “磁头” 到目标 扇区

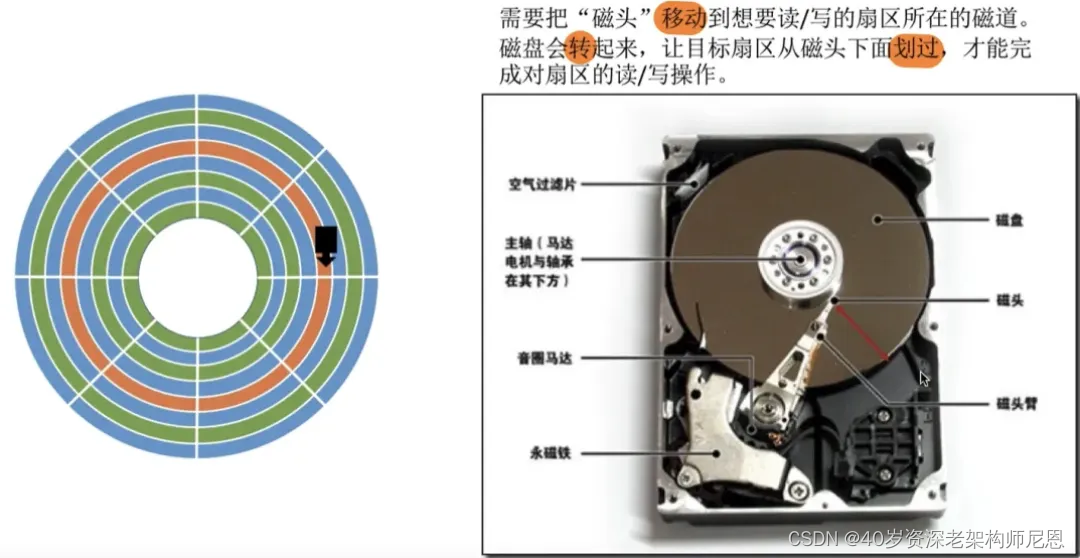
机械磁盘的读写以扇区为基本单位。

硬盘的物理读写以扇区为基本单位。通常情况下每个扇区的大小是 512 字节。

然而，今天的应用程序是写入密集型的，并且会生成大量数据。因此，需要重新考虑 DBMS 中现有存储引擎的设计。

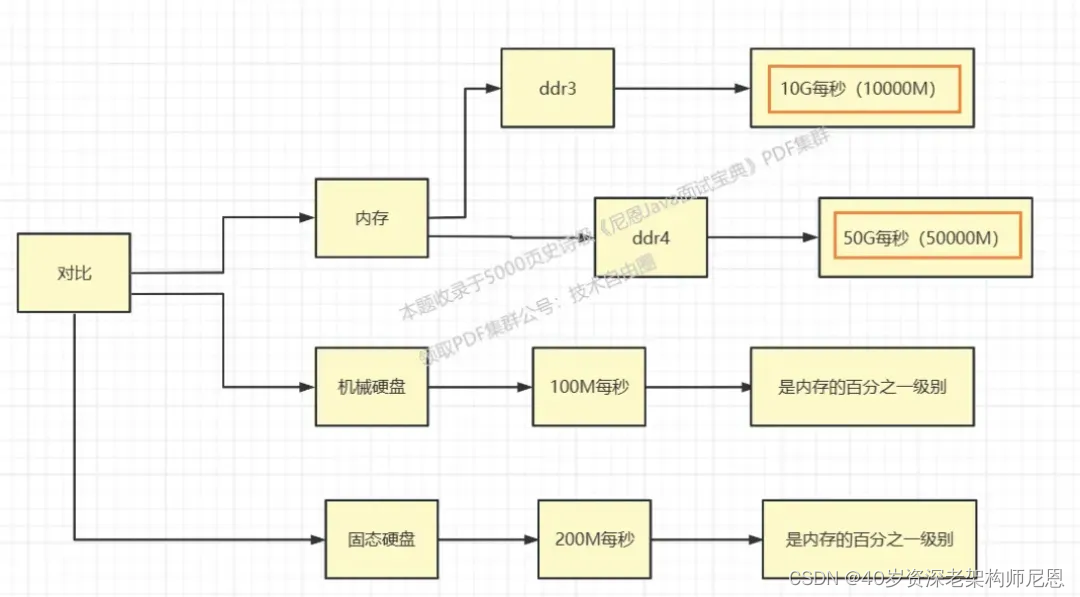
内存和磁盘的访问速度对比

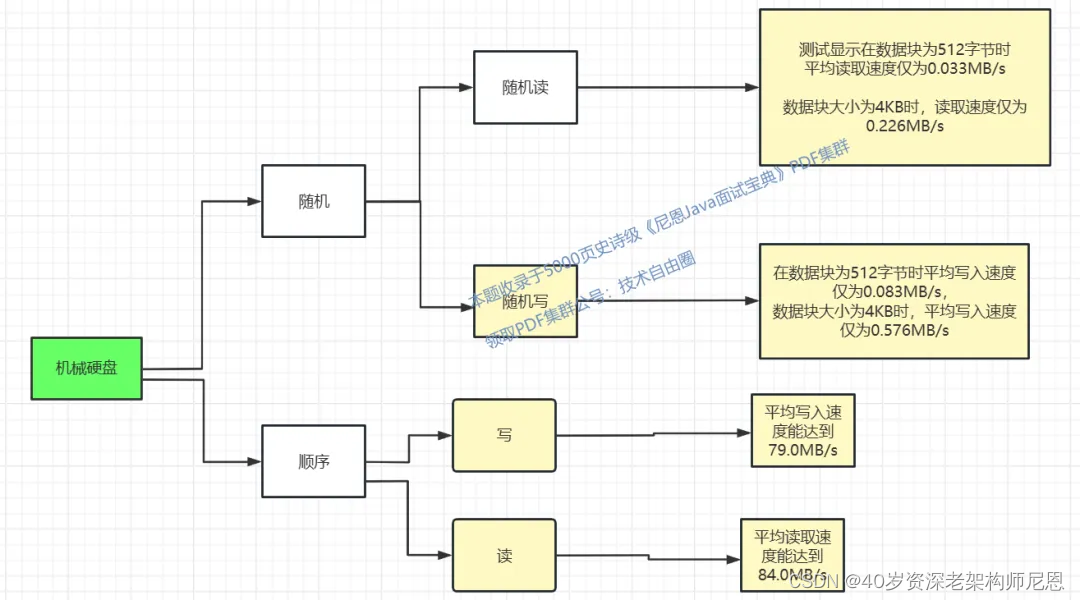
机械硬盘的读写速度，大致如下

固态硬盘的读写速度，大致如下

性能比较-机械硬盘

机械硬盘在顺序读写场景下有相当出色的性能表现，但一遇到随机读写性能则直线下降。

顺序读是随机读性能的400倍以上。顺序读能达到84MB/S。

顺序写是随机读性能的100倍以上。顺序写性能能达到79M/S。

原因：是因为机械硬盘采用传统的磁头探针结构，随机读写时需要频繁寻道，也就需要磁头和探针频繁的转动，而机械结构的磁头和探针的位置调整是十分费时的，这就严重影响到硬盘的寻址速度，进而影响到随机写入速度。

性能比较-SSD固态硬盘

顺序读：220.7MB/s。随机读：24.654MB/s。 顺序写：77.2MB/s。随机写：68.910MB/s。

总结：对于固态硬盘，顺序读的速度仍然能达到随机读的10倍左右。但是随机写还是顺序写，差别不大。

HDD机械硬盘和SSD固态 硬盘性价比

1、固态硬盘（SSD），优点：读取速度快、抗震性强、功耗低、运行安静。缺点：价格较高、写入寿命有限、容量较小。

2、机械硬盘（HDD），优点：价格低廉、大容量、写入寿命长。缺点：读取速度慢、抗震性差、功耗高、运行噪音大。

选择适合的硬盘需考虑具体需求，如性能需求选SSD，大容量存储选HDD。

像HBASE这样的 海量存储集群，一般都选择 HDD。

在 HDD 的硬件基础上， B+树的写入性能低， 那么 LSM树 就是为 写 而生。

LSM树 就是为 写 而生。

LSM树 就是为 写 而生。

LSM树 就是为 写 而生。

当然， 真实的海量存储中间件，也会对读进行性能优化， 比如引入 布隆过滤器。

布隆过滤器的事情后面再说，咱们言归正传。

什么是LSM树

LSM树，即日志结构合并树(Log-Structured Merge-Tree)。其实它并不属于一个具体的数据结构，它更多是一种数据结构的设计思想。

大多NoSQL数据库核心思想都是基于LSM来做的，或者说，几乎所有 NoSQL 数据库都使用 LSM Tree 的变体作为其底层存储引擎，因为它允许它们实现快速的写入吞吐量和对主键的快速查找。

LSM-Tree 全名叫Log-Structured Merge Tree，最早建立在日志结构文件之上，现在基于合并和压缩排序文件原理的存储引擎都统称为LSM存储引擎。

我们通常把LSM看成一种思想：保存在后台合并的一系列SStable

这种思想简单且有效：

• 即使数据集远大于内存，LSM-tree也能正常工作
• 由于键值有序，范围查询相比于hash表有很大优势
• 由于写入是顺序的（归并是后台线程在空闲时间做的）,所以可以提供非常高的写入吞吐量

查找的性能优化：

在LSM系统中查找一个不存在的键时会导致查询时间长，因为要从最新的数据一直往前查找，所以LSM一般会使用布隆过滤器进行优化

接下来，在介绍LSM 之前，先说说 SSTable

SSTables 四大操作流程

LSM tree 通过一种叫做 SSTable (Sorted Strings Table) 的格式，持久化到硬盘上。

顾名思义，SSTable 是一种用来存储有序的键值对的格式，其中键 是有序存储的。

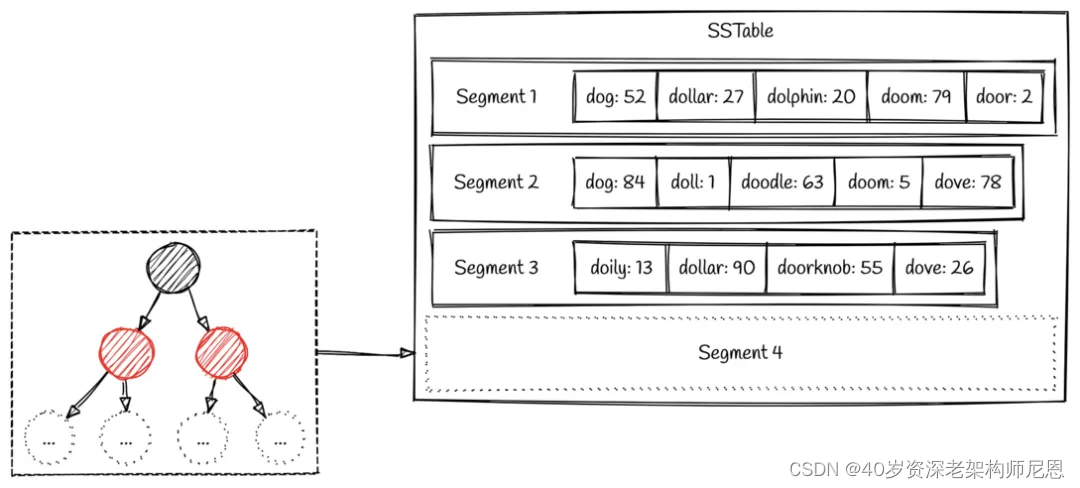
一个SSTable 会包括多个有序的子文件，被称为 segment 。

这些 segments 一旦被写入硬盘，就不可以再修改了。

一个简单的SSTable 例子如下图所示：

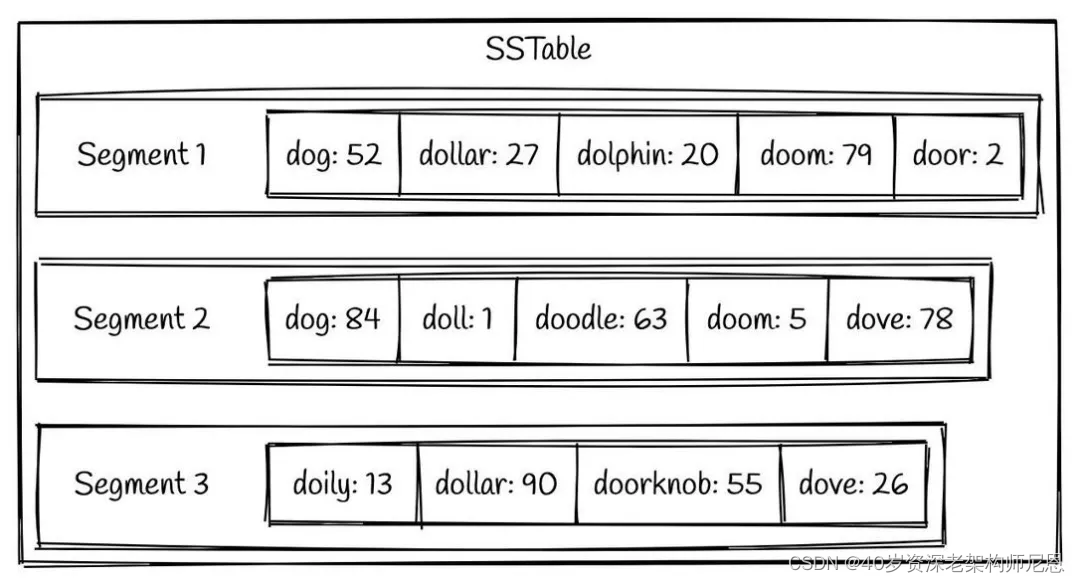
我们可以看到，在每个 segment 中的键值对都是按照键的顺序有序组织的。

SSTables 写入数据的基本流程

由于 LSM tree 只会进行顺序写入，所以自然而然地就会引出这样一个问题：

写入的数据可能是任意顺序的，我们又如何保证数据能够保持 SSTable 要求的有序组织呢？

这就需要引入新的常驻内存 (in-memory) 数据结构: memtable_table,

memtable_table 的底层数据结构则有点像红黑树,当由新的写入操作则将数据插入到红黑树中。

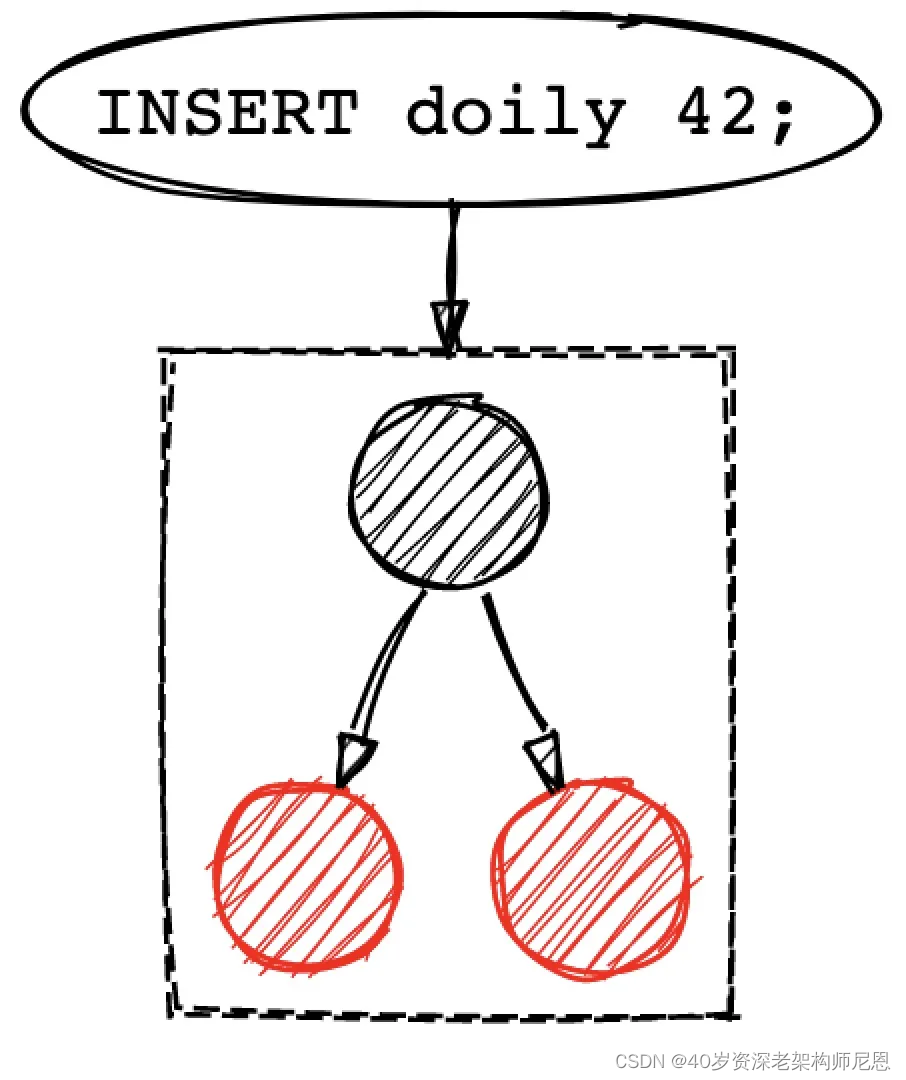
写入操作会先把数据存储到红黑树中，直至红黑树的大小达到了预先定义的大小。

一旦红黑树的大小达到阈值，就会把数据整个刷到磁盘中，这个过程就可以把数据保证有序写入了。

经过一层数据结构的承接，就可以保证单向顺序写入的同时，也能保证数据的有序了。

SSTables 读取数据的基本流程

那么我们是如何从SSTable中查找数据的呢？

一种naive的方法就是遍历所有的 segments，寻找我们需要的key。

从最新的 segment 到最老的 segment 一一遍历，知道找到目标key为止。

显然，这种方式在寻找刚刚写入的数据是比较快的，但是文件一多就不太行了。

针对这个问题，如何的优化？

需要引入索引：比如 跳表、比如 稀疏索引。不同的索引，根据不同设计具体选择。

先看看简单的 稀疏索引。

稀疏索引就是一种在内存中对数据检索进行优化的技术。