LeetCode No.450 删除二叉搜索树中的节点

最新推荐文章于 2025-09-07 19:28:08 发布

原创最新推荐文章于 2025-09-07 19:28:08 发布 · 138 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #二叉搜索树 #递归

LeetCode Hot 100 专栏收录该内容

86 篇文章

订阅专栏

本文介绍了一种从二叉搜索树中删除指定节点的方法。根据节点的不同情况（叶子节点、仅有一个子节点或有两个子节点），采取不同策略进行删除。对于非叶子节点，会寻找替代值以保持树的有序性。

在这里插入图片描述

结果还是相当棒的

思路：
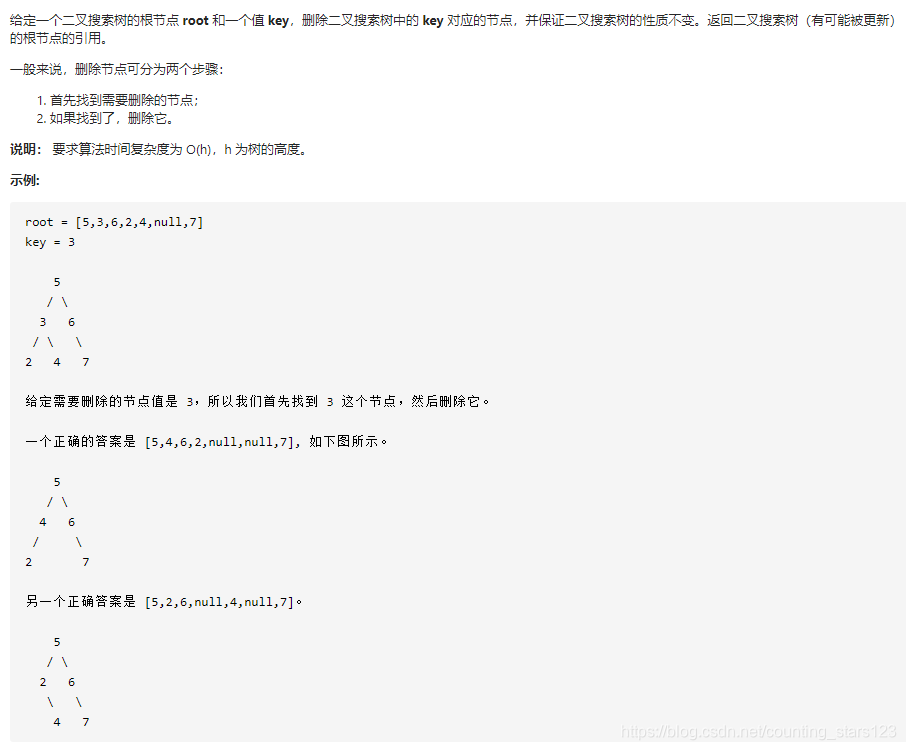
首先考虑，当一个二叉搜索树中一个节点被删除之后，我们应该先看它是不是叶子节点，如果是叶子节点，就直接删去它（递归）。
如果它有左子树，那就找到它左子树中的最大值，将最大值赋给它，然后删除左子树中的最大值（递归）。
如果它没有左子树但有右子树，那就找到它右子树中的最小值，将最小值赋给它，然后删除右子树中的最小值（递归）。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */


 //先找到该节点
 //找到该节点后，分为三种情况：1.该节点为叶子节点 2.该节点只有左子树或右子树 3.该节点有左子树也有右子树
 
class Solution {

    public TreeNode find(TreeNode root, int key)//找到值为key的节点，如果找到就返回该节点，找不到就返回null
    {
        if(root==null) return null;
        if(root.val==key) return root;
        TreeNode l = find(root.left,key);
        TreeNode r = find(root.right,key);
        return (l!=null)?l:r;
    }


    public TreeNode deleteNode(TreeNode root, int key) {//删除值为key的节点，并返回根节点
        if(root==null)
        {
            return null;
        }
        if(root.val==key&&root.left==null&&root.right==null)
        {
            return null;
        }
        TreeNode node = find(root,key);//找到该节点
        if(node==null)//如果找不到，不做改变，返回root
        {return root;}
        if(node.left!=null)//如果node的左子树不为空
        {
            TreeNode p = node.left;
            while(p.right!=null)//找到左子树中的最大值节点p
            {
                p = p.right;
            }
            node.val = p.val;//将p的值赋给node
            node.left = deleteNode(node.left,p.val);//删除左子树中的p,并返回左子树根节点,重置为node的左子树
            return root;//删除完node之后，返回root
        }
        if(node.right!=null)//如果node的左子树为空,右子树不为空
        {
            TreeNode p = node.right;
            while(p.left!=null)//找到右子树中的最小值节点p
            {
                p = p.left;
            }
            node.val = p.val;//将p的值赋给node
            node.right = deleteNode(node.right,p.val);//删除node右子树中的p,并返回右子树根节点,重置为node的右子树
            return root;
        }
        if(node.left==null&&node.right==null)//如果node为叶子节点
        {
            root.left = deleteNode(root.left,node.val);//root的左子树删除node,并返回删除后的左子树根节点,重置为root的左子树
            root.right = deleteNode(root.right,node.val);//root的右子树删除node,并返回删除后的右子树根节点,重置为root的右子树
            //注意，如果没有找到该节点，会不做任何修改直接返回根节点
        }
        return root;
    }
}