LeetCode No.144 二叉树的前序遍历

最新推荐文章于 2025-09-05 15:52:23 发布

原创最新推荐文章于 2025-09-05 15:52:23 发布 · 115 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #二叉树 #栈

LeetCode Hot 100 专栏收录该内容

86 篇文章

订阅专栏

这篇博客详细介绍了二叉树的前序、中序和后序遍历的Java实现，并通过一个通用的遍历套路进行解释。在遍历过程中，使用了指针p和变量last来跟踪当前遍历状态，确保正确遍历左子树和右子树。文章还对比了三种遍历方式在何时输出节点值和何时弹栈的区别，帮助理解二叉树遍历的基本逻辑。

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：
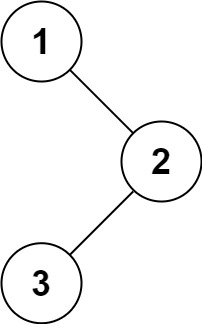
在这里插入图片描述

输入：root = [1,null,2,3]
输出：[1,2,3]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [1]
输出：[1]

示例 4：
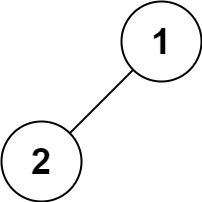
在这里插入图片描述

输入：root = [1,2]
输出：[1,2]

示例 5：
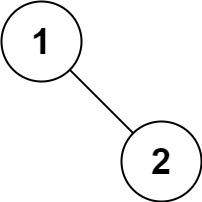
在这里插入图片描述

输入：root = [1,null,2]
输出：[1,2]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {//前序
        TreeNode p = root;//p用来记录当前栈顶左子树是否还需要遍历
        LinkedList<TreeNode> stack = new LinkedList<>();
        TreeNode last = null;//last用来记录前一个遍历完的子树根节点（前一个pop的节点）
        List<Integer> l = new ArrayList<>();
        while(p!=null||!stack.isEmpty())
        {
            if(p!=null)
            {
                stack.push(p);
                System.out.println(p.val);//前序最大的特点就是入栈时候就输出节点的值
                l.add(p.val);
                p = p.left;
            }
            else
            {

                if(stack.peek().right==null||stack.peek().right==last)
                {
                    last = stack.pop();

                }
                else
                {
                    p = stack.peek().right;

                }

            }

        }
        return l;

    }
    
    public List<Integer> back(TreeNode root) {//后序
        TreeNode p = root;//p用来记录当前栈顶左子树是否还需要遍历
        LinkedList<TreeNode> stack = new LinkedList<>();
        TreeNode last = null;//last用来记录前一个遍历完的子树根节点（前一个pop的节点）
        List<Integer> l = new ArrayList<>();
        while(p!=null||!stack.isEmpty())
        {
            if(p!=null)
            {
                stack.push(p);
                p = p.left;
            }
            else
            {

                if(stack.peek().right==null||stack.peek().right==last)
                {
                    last = stack.pop();//栈顶左子树为空或已遍历完，右子树也已遍历完或为空，则pop栈顶
                    System.out.println(last.val);
                    l.add(last.val);

                }
                else
                {
                    p = stack.peek().right;

                }

            }

        }
        return l;

    }
    
     public List<Integer> midTree(TreeNode root)//中序
    {
        TreeNode p = root;//p用来记录当前栈顶左子树是否还需要遍历
        LinkedList<TreeNode> stack = new LinkedList<>();
        List<Integer> l = new ArrayList<>();//保存遍历结果
        TreeNode last = null;//last用来记录前一个遍历完的子树根节点（前一个pop的节点）
        while(p!=null||!stack.isEmpty())
        {
            if(p!=null)
            {
                stack.push(p);
                p = p.left;
            }
            else
            {

                if(stack.peek().right!=last&&stack.peek().right!=null)
                {
                    p = stack.peek().right;

                }
                last = stack.pop();//中序遍历的特点是左子树一为空或一遍历完就马上pop栈顶
                System.out.println(last.val);
                l.add(last.val);

            }

        }
        return l;

    }
}

二叉树的遍历有一个套路，就是都需要一个指针p，当p不为空时候将p入栈，然后p=p.left，进入下一轮循环，先一股脑走到左边到头。还需要一个变量last来记录之前pop的节点。
然后每当pop的时候，都将p置为空。然后当p为空的时候就说明当前栈顶节点的左子树为空，或者左子树已经遍历完。所以p就是用来判断当前栈顶的左子树是否需要遍历的，而p不为空的时候永远指向当前栈顶的左节点，说明当前栈顶的左节点还没有遍历，需要push进栈。
我们每次pop的时候，这个节点相对于他的根节点可能是左节点，也可能是右节点。那么因为不管前序，中序，后序遍历，左子树都先比右子树遍历完。那么如果这个节点是左节点，则正好令p为null,向下一个根节点表明它的左子树已经遍历完了，如果这个节点是右节点，则说明在它之前左节点也一定已经遍历完了。所以pop操作后面一定跟着要将p置为null。然后下一轮循环，栈顶节点就会知道，哦，我的左子树已经遍历完了。
我们用p来判断左子树是否遍历完或是否为空，如何判断当前栈顶的右子树是否遍历完呢？
我们需要一个变量last来记录之前pop的节点。每次pop之后，都将last指向pop出去的节点。
当p==null时，说明左子树都遍历完了或不需遍历，那么我们就判断一下栈顶节点的右子树是否为空或是否和last一致。如果右子树为空则说明栈顶的右子树不需要遍历，如果右子树和last一样说明右子树刚刚遍历完。

这样，在一轮循环中，我们就可以通过p来判断当前栈顶的左子树是否遍历，也可以通过last来判断当前节点的右子树是否被遍历。总体架构都是完全一样的。
前序，中序，后序的区别关键在于什么时候输出，和什么时候pop。
前序是入栈push的时候输出节点值，中序和后序都是出栈pop的时候输出节点值。
前序和后序都是当栈顶的右子树已经遍历完或右子树为空的时候pop,中序则是左子树一为空或一遍历完就马上pop栈顶节点。
其实总得来说，二叉树的遍历基本都是先根，再左子树，再根，再右子树的路径，只不过遍历的结果和什么时候输出根节点的值有关。