Reinforcement Learning An Introduction~A k-armed Bandit Problem

最新推荐文章于 2024-05-14 18:26:39 发布

翻译最新推荐文章于 2024-05-14 18:26:39 发布 · 378 阅读

文章标签：

#强化学习

Reinforcement learning 专栏收录该内容

12 篇文章

订阅专栏

本文围绕强化学习中的k臂赌博机问题展开。强化学习使用评价反馈，与监督学习的指导反馈不同。k臂赌博机问题中，每次选择动作后会获奖励，目标是最大化总回报。还探讨了探索与利用的冲突，提出几种简单平衡方法，比常用方法更有效。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Chapter 2 多臂赌博机

区分强化学习与其他类型学习的最重要特征是它使用训练信息来评估所采取的行动而不是通过给出正确的行动来指导。这就是积极探索创造需求，以明确寻找较好的动作。纯粹的评价反馈表明所采取的动作有多好，但不表明它是最好还是最坏的动作。另一方面，纯粹的指导性反馈表明采取的动作是正确的，但与实际采取的行动无关。这种反馈是监督学习的基础，包括模式分类，人工神经网络和系统识别中的大部分。在它们各自的纯粹形式中，这两种反馈是截然不同的：评价反馈完全取决于所采取的动作，而指导性反馈则与所采取的动作无关。

在本章中，我们在简化的环境中研究强化学习的评价方面，该方法不涉及学习在面对多种情况下的行动。这种非关联性设置是大多数先前涉及评估反馈的工作已经完成的，并且它避免了完整强化学习问题的大部分复杂性。研究这个案例使我们能够最清楚地看到评价反馈的不同之处，并且也可以与指导性反馈相结合。

我们探索的特定非关联性，评价性反馈问题是k臂赌博机问题的简单版本。我们用这个问题来介绍，一些我们在后面章节中适用于完整的强化学习问题的扩展的基本学习方法。在本章的最后，我们通过讨论当强盗问题变成联想问题时，也就是在不止一种情况下采取行动时，会发生什么，从而更接近于完全强化学习问题。

2.1 一个k臂赌博机问题

考虑下面的学习问题。你不断面临k个不同的选择，或者说是动作。每一次选择之后，你都会从一个固定的概率分布中得到一个数字奖励，这个概率分布取决于你所选择的动作。您的目标是在一段时间内最大化期望的总回报，例如，超过1000个动作选择或时间步骤。

这是k臂赌博机问题的原始形式，通过类比于插槽机或“单臂赌博机”命名，除了它有k个控制杆而不是一个之外并无什么不同。每个动作选择就像一个选择赌博机的控制杆游戏，奖励是击中累积奖金的回报。通过反复的动作选择，通过将你的动作集中在最好的控制杆上，您将最大化您的奖励来赢得奖金。另一个类比是医生在一系列重病患者的实验性治疗之间进行选择。每个动作都是治疗的选择，每个奖励都是患者的生存或幸福。今天，术语“赌博机问题”有时用于上述问题的概括，但在本书中我们用它来指代这个简单的情况。

在我们的k臂赌博机问题中，因为选择了某个动作，k个动作中的每一个动作都有预期的或平均的奖励; 我们称之为该动作的价值。我们将在时刻t选择的动作表示为 $A_{t}$ ，并将相应的奖励表示为 $R_{t}$ 。然后，任意动作a的价值，表示为 $q_{*}\left ( a \right )$ ，是给定a选择的预期奖励：

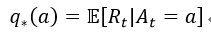
如果你知道每个动作的价值，那么解决k臂赌博机问题将是微不足道的：你总是选择具有最高价值的动作。尽管您可能有估计值，但我们假设您明确地不知道动作值。我们将在时刻t的动作a的估计值表示为 $Q_{t}\left ( a \right )$ 。我们希望 $Q_{t}\left ( a \right )$ 接近 $q_{*}\left ( a \right )$ 。

如果您保持对动作价值的估计，那么在任何时刻都至少有一个估计值最大的动作。我们称之为贪婪的行为。当您选择其中一个动作时，我们会说您正在利用您当前对动作价值的了解。相反，如果你选择了一个非贪婪动作，那么我们就说你正在探索，因为这可以让你提高你对非行动动作价值的估计。利用是最好的方法，可以在一步中最大化预期的奖励，但从长远来看，探索可能会产生更大的总回报。例如，假设贪婪行为的价值已确定，而其他一些行动估计几乎同样好但具有很大的不确定性。不确定性使得这些其他行动中的至少一个实际上可能比贪婪行动更好，但你不知道哪一个。如果你有很多时刻为了做出行动选择，那么探索非贪婪行动并发现哪些行动比贪婪行动更好可能更好。在短期内，奖励在探索期间较低，但从长远来看更高，因为在您发现更好的行动之后，您可以多次利用它们。因为任何单一行动无法同时选择探索和利用，人们通常会提到在探索和开发之间的“冲突”问题。

在任何具体情况下，探索或利用哪一个更好，取决于复杂方式：估计值的精确，不确定性和剩下的时刻步数。有许多复杂的方法可以平衡探索和利用k臂赌博机问题中的特定数学公式和相关问题。然而，这些方法中的大多数都对平稳性和先验知识做出了强有力的假设，这些假设要么被违反，要么无法在应用程序中得到验证，要么无法在我们后面章节中考虑的完全强化学习问题中得到验证。当这些方法的理论假设不适用时，这些方法的最优性或有界损失的保证就没有什么意义了。在本书中，我们并不担心如何以一种复杂的方式平衡探索和利用;我们只担心如何平衡它们。在这一章中，我们提出了几种简单的平衡k臂赌博机问题的方法，并证明它们比通常使用的方法更有效。在强化学习中，平衡探索和利用的需要是一个独特的挑战;我们对k臂赌博机问题的简单看法使我们能够以一种特别清楚的形式表明这一点。