【LeetCode-剑指offer】

题目描述：

      给你 n 个二维平面上的点 points ，其中 points[i] = [xi, yi] ，请你返回两点之间内部不包含任何点的 最宽垂直区域 的宽度。

垂直区域 的定义是固定宽度，而 y 轴上无限延伸的一块区域（也就是高度为无穷大）。 最宽垂直区域 为宽度最大的一个垂直区域。

请注意，垂直区域 边上 的点 不在 区域内。

 

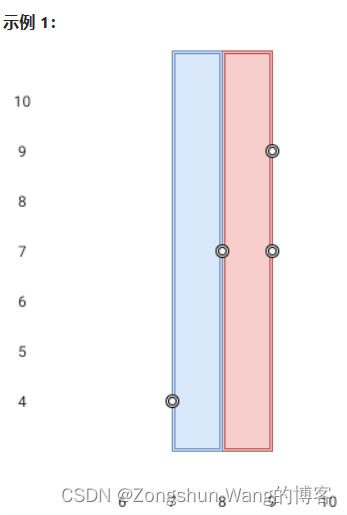
输入：points = [[8,7],[9,9],[7,4],[9,7]]
输出：1
解释：红色区域和蓝色区域都是最优区域。

示例2：

输入：points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
输出：3

提示： 

• n == points.length
• 2 <= n <= 105
• points[i].length == 2
• 0 <= xi, yi <= 109

题目解答：

这是一道求解「最大间隔」问题的题目。题目中给出了一些二维平面上的点，在垂直方向上，这些点之间的间隔是无限大的，所以我们需要找到在x轴上最大的间隔，即相邻两个点之间的距离的最大值。

算法思路：

1. 将所有点按照 x 坐标进行排序，这里我们采用桶排序算法，时间复杂度为O(n)

2. 遍历排序后的数组，计算相邻两个点之间的距离，并找出距离的最大值，即可得到最宽垂直区域的宽度。

以下是基于 C 语言的程序实现：

int maxWidthOfVerticalArea(int** points, int pointsSize, int* pointsColSize){
    int x[MAX_POINTS];
    int i, max = 0;
    
    /* 将所有点按照 x 坐标进行排序 */
    for (i = 0; i < pointsSize; i++) {
        x[i] = points[i][0];
    }
    bucketSort(x, pointsSize);

    /* 遍历排序后的数组，计算相邻两个点之间的距离 */
    for (i = 1; i < pointsSize; i++) {
        if (x[i] - x[i-1] > max) {
            max = x[i] - x[i-1];
        }
    }
    
    return max;
}

在该程序中，我们声明了一个数组 x，并使用桶排序算法将所有点按照 x 坐标进行排序。然后，我们遍历数组，计算相邻两个点之间的距离，并找到距离的最大值，即可得到最宽垂直区域的宽度。最后，程序返回最大的间隔，即为最宽垂直区域的宽度。

需要注意的是，由于输入的点数可能很大，我们需要使用较为高效的排序算法来对输入数据进行排序。在这里，我们选择使用桶排序算法对 x 坐标进行排序，时间复杂