回溯法 | 求解装载问题

问题描述：

有 n 个集装箱要装上一艘载重量为 W 的轮船，其中集装箱 i (1<=i<=n) 的重量，为wi。子啊装在体积不受限制的情况下，将尽可能重的集装箱装上轮船，当重量相同时要求选取的集装箱个数尽可能少，编写一个实验程序采用回溯法求解。要求采用适当的剪枝条件提高效率，左孩子结点剪枝的条件是只装载满足重量要求的集装箱，右孩子结点剪枝的条件是至多要选中 3 个集装箱。

例如，n=5，W=10，w[] = {5,2,6,4,3}时，其最佳装载方案是(0,0,1,1,0)，既装载第3、4个集装箱。

问题分析：

看完题目感觉可以用穷举法把所有可能性全列举出来，然后从所有结果中选取一个最优解，然后输出。

but，题目需要回溯法，那么就要考虑用回溯法的思想去解决这个问题。

回溯法：在包含问题的所有解的解空间树中，按照深度搜索优先的策略，从根节点出发搜索解空间树。

下图展示的是程序的大致执行过程。

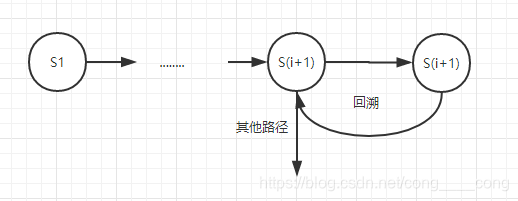
简单的说就是一直在深度优先搜索结果，查找完当前层的时候需要恢复以前修改数据，保证接下来深度搜索基准数据没有错。

如果只是简单的回溯，其实和穷举法差不多，但是 回溯法中可以写剪枝函数，把那些不满足条件的枝叶剪掉，从而加快搜索速度。

下面我们来模拟一遍回溯的过程，假设现在w[] 这个数组中只有3个元素，分别为 5 、2、6

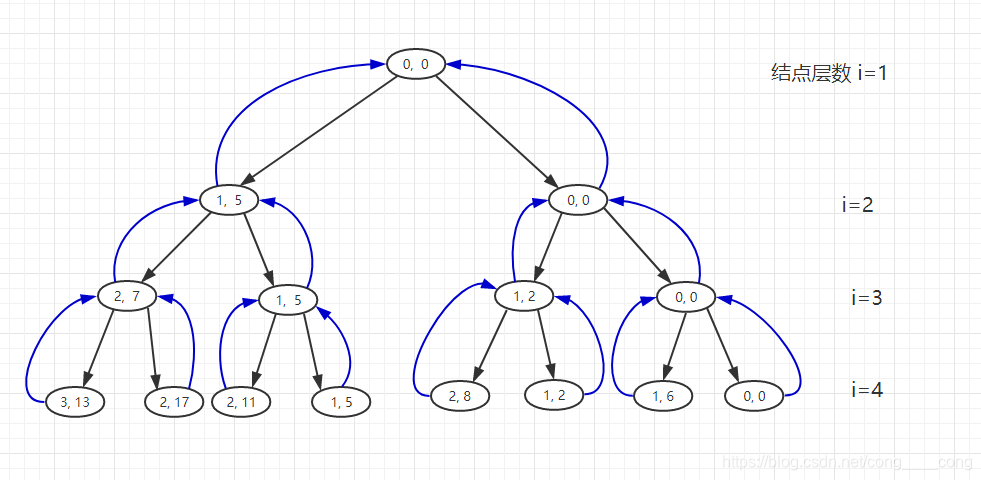
图中黑色直线标识深度递归到某一层进行计算，蓝色的线条表示当