区间DP三步曲

区间DP

这里选取了区间DP非常有代表性的三道题，三题之间层层递进，有助于理解好区间DP

区间DP常用代码模板，点击链接或如下：

for (int len = 1; len <= n; len++) {         // 区间长度
    for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
        int j = i + len - 1;                 // 区间终点
        if (len == 1) {
            f[i][j] = 初始值
            continue;
        }

        for (int k = i; k < j; k++) {        // 枚举分割点，构造状态转移方程
            f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + w[i][j]);
        }
    }
}

石子合并

《算法竞赛进阶指南》石子合并

• 状态表示$f[i,j]$：从第i堆石子到第j堆石子合并所需的代价
• 状态计算：将区间划分成$[i,k]$和$[k+1,j]$，$k=i,i+1,...,j-1$

通过枚举区间长度，找出代价的最小值

状态转移：$f[l][k]+f[k+1][r]+s[r]-s[l-1]$

最后一次转移加上它的代价

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310;
int n;
int f[N][N];
int s[N];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &s[i]);
    // 前缀和，确定任一区间的权重
    for (int i = 1; i <= n; i ++ ) s[i] += s[i-1];
    
    // len=1的时候无须合并，所以从2开始
    for (int len = 2; len <= n; len++)			// 区间长度
        for (int i = 1; i + len - 1 <= n; i++) {// 枚举起点
            int l = i, r = i + len -1;
            f[l][r] = 1e8;
            // 在区间范围内进行划分
            for (int k = l; k < r; k++) // 不能取等，要保证右边至少有一个才有得合并
                f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]);
        }
    
    cout << f[1][n] << endl;
    
    return 0;
}

密码脱落

第七届蓝桥杯省赛C++A/C组-密码脱落

给定一个现在看到的密码串，计算一下从当初的状态，它要至少脱落多少个种子，才可能会变成现在这样

原先至少脱落多少的种子=现在再脱落多少的种子=总长度-最大回文子序列

最大回文子序列状态分析

图片原地址

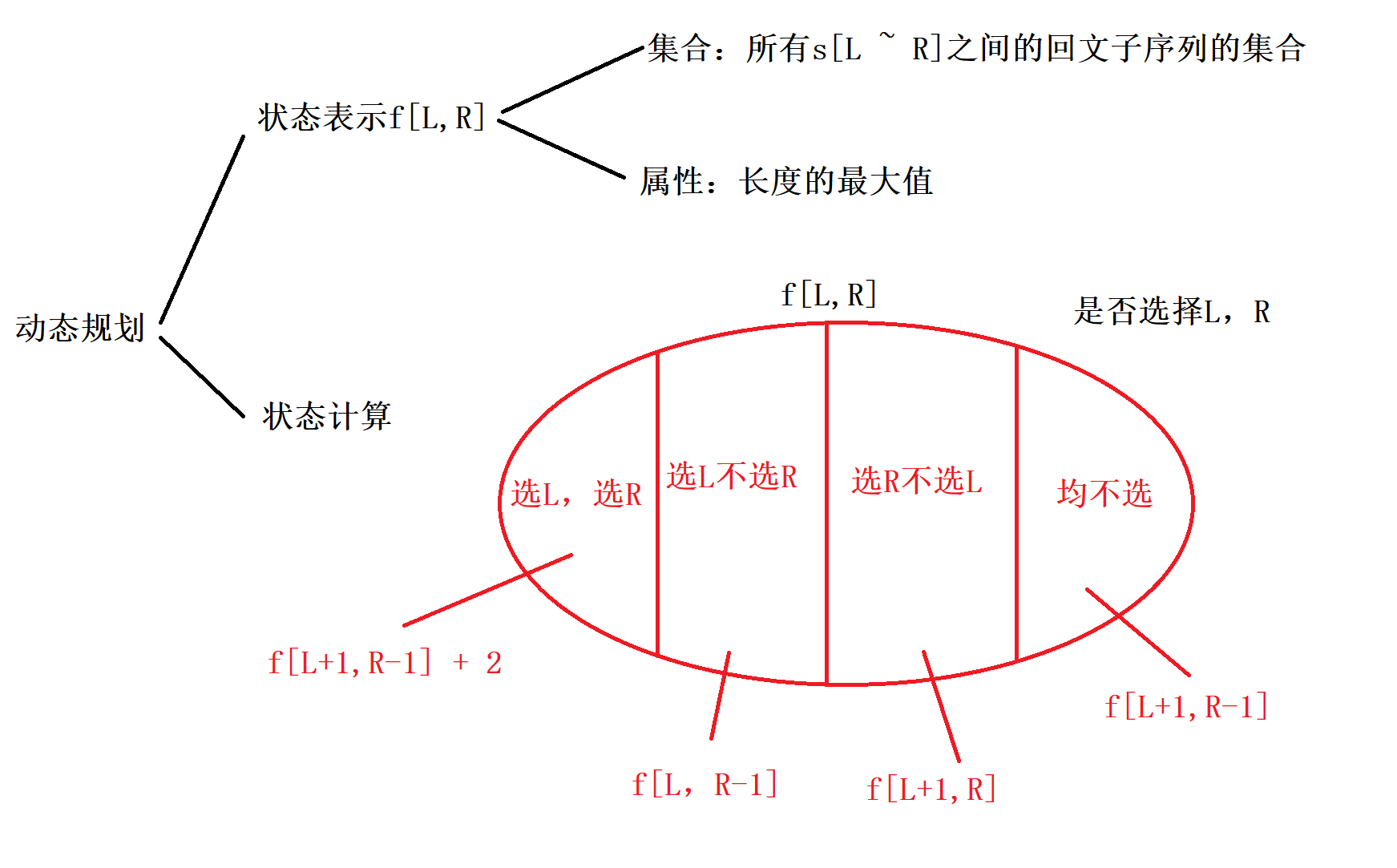
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int N = 1010;
char str[N];
int f[N][N];

int main() {
    scanf("%s", str);
    int n = strlen(str);
    for (int len = 1; len <= n; len++) {
        for (int l = 0; l + len - 1 < n; l++) {
            int r = l + len - 1;
            if (l == r) f[l][r] = 1;
            else {
                if (str[l] == str[r]) f[l][r] = f[l+1][r-1] + 2;
                if (f[l+1][r] > f[l][r]) f[l][r] = f[l+1][r];
                if (f[l][r-1] > f[l][r]) f[l][r] = f[l][r-1];
            }
        }
    }
    cout << n - f[0][n-1] << endl;
    
    return 0;
}

括号配对

密码脱落+石子合并结合版

《信息学奥赛一本通》- 括号配对

以下是 GBE 的定义：

• 空表达式是 GBE
• 如果表达式 A 是 GBE，则 [A] 与 (A) 都是 GBE
• 如果 A 与 B 都是 GBE，那么 AB 是 GBE（区别于普通回文串的地方）

下面给出一个 BE，求至少添加多少字符能使这个 BE 成为 GBE。

---

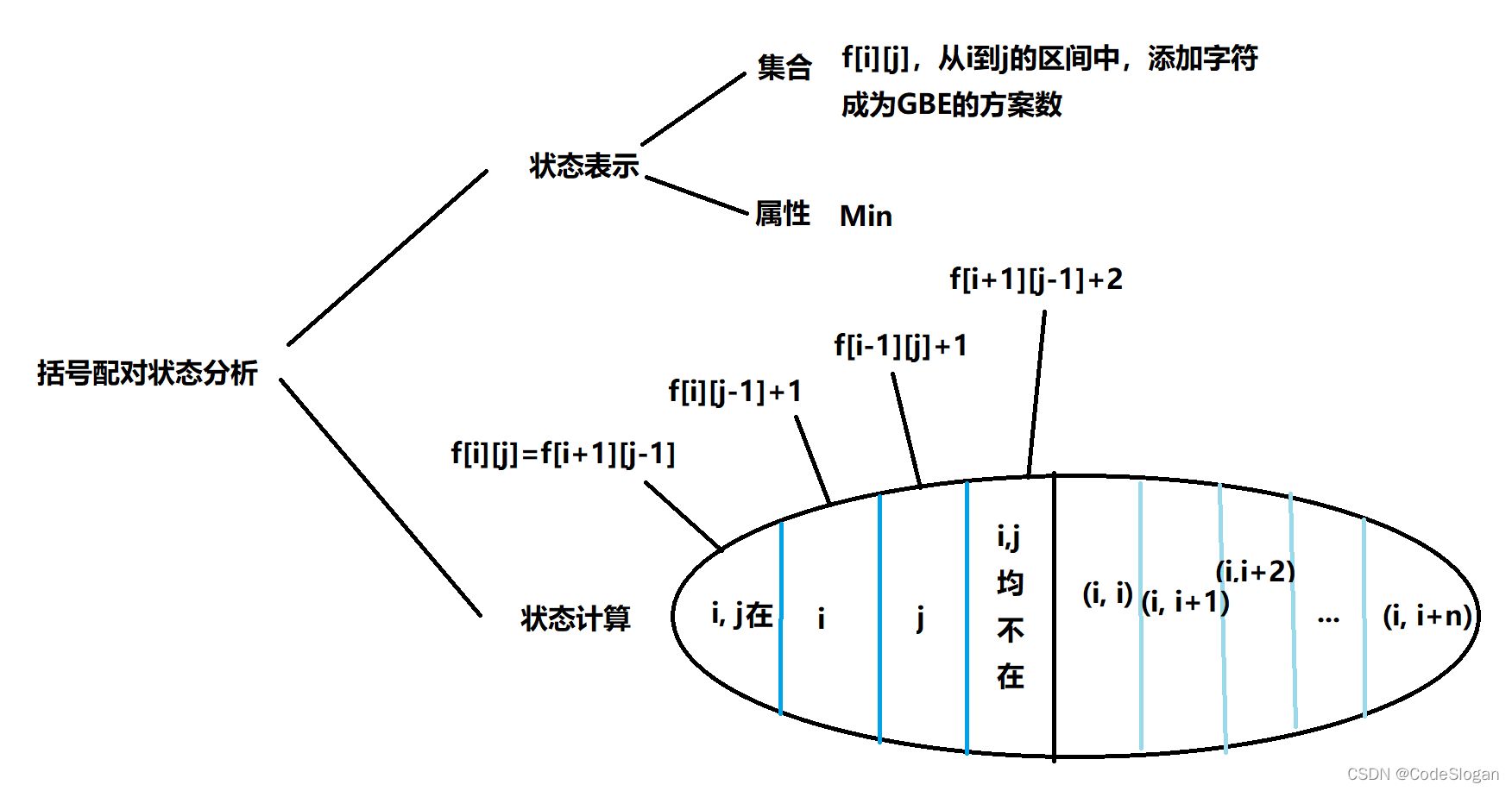
状态计算分析

左半边

• i、j都被用上，即i、j匹配成功，是左右括号关系，那么要求添加多少字符应该进一步到f[i+1][j-1]当中求解
• 如果i,j有一个不在最终GBE中，即需要一个字符与它匹配，会等于f[i+1][j]+1。这一步会有一个状态包含关系，详情请见石子合并

右半边

• 左边第一个完整括号的长度
• 假设此时[i,k]匹配成功了，那么最小值等于f[i][k]+f[k+1][j]。这里依旧有个包含关系，因为深入到[i,k]当中，可能仍有不完整的符号

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110, INF = 1e9;
int f[N][N];

bool is_match(char l, char r) {
    if (l == '(' && r == ')') return true;
    if (l == '[' && r == ']') return true;
    return false;
}

int main() {
    string str;
    cin >> str;
    int n = str.size();
    if (n == 1) { // 特判
        cout << 1 << endl;
        return 0;
    }
    
    for (int len = 1; len <= n; len++) {
        for (int l = 0; l + len - 1 < n; l++) {
            int r = l + len - 1;
            f[l][r] = INF;
            if (is_match(str[l], str[r])) f[l][r] = f[l+1][r-1];
            if (r >= 1)
                f[l][r] = min(f[l][r], min(f[l+1][r], f[l][r-1]) + 1);
            for (int k = l; k < r; k++)
                f[l][r] = min(f[l][r], f[l][k] + f[k+1][r]); 
        }
    }
    cout << f[0][n-1] << endl;
    
    return 0;
}