sheng的学习笔记-AI基础-正确率/召回率/F1指标/ROC曲线

AI目录：sheng的学习笔记-AI目录-优快云博客

分类准确度问题

假设有一个癌症预测系统，输入体检信息，可以判断是否有癌症。如果癌症产生的概率只有0.1%，那么系统预测所有人都是健康，即可达到99.9%的准确率。

但显然这样的机器学习系统是失败的，因为对于极度偏斜(Skewed Data)的数据，只使用分类准确度是远远不够的。

针对这样的问题，我们需要引入其他指标来评估机器学习分类结果的好坏。

混淆矩阵

对于二分类问题，混淆矩阵是2x2，分别是0和1，其中每一行代表真实值，每一列代表预测值

TP：True Positive。预测为1，实际为1，预测正确。
FP：False Positive。预测为1，实际为0，预测错误。
FN：False Negative。预测为0，实际为1，预测错误。
TN：True Negative。预测为0，实际为0，预测正确。

指标

取值范围

这几个指标的取值都在0-1之间，数值越接近于1，效果越好

精度

预测数据中预测正确的数量就是精准率，检索出来的条目有多少是正确的

召回率

真实发生数据预测正确的数量就是召回率，所有正确的条目有多少被检索出来

F1Score

F1Score指标就是综合精准率和召回率两个指标，只有当召回率和精度都很高时，分类器才能得到较高的F1分数

ROC曲线

ROC（Receiver Operating Characteristic，受试者工作特征）曲线是一种反映分类模型在不同阈值下性能的图形工具。它以假正例率（False Positive Rate, FPR）为横轴，真正例率（True Positive Rate, TPR）为纵轴，描绘模型的分类能力。

引入两个指标，误报率(FPR)和召回率(TPR)。

其中FPR = $\frac{FP}{TN+FP}$ ，它是指是被错误地预测为正类的样本占所有实际为负类的样本的比例。TPR = $\frac{TP}{TP+FN}$ ，它是指被正确地预测为正类的样本占所有实际为正类的样本的比例。

绘制ROC曲线的步骤

1. 计算模型预测概率

让模型对测试集进行预测，得到每个样本属于正类的概率或评分。

2. 设定阈值

选择一系列从1到0的阈值，用于将预测概率转化为具体的类别标签。分类问题，一般情况下默认阈值为0.5。

3. 计算TPR和FPR

将阈值按照从高到低排序，对于每个阈值下的类别标签，计算对应的TPR和FPR。

4. 绘制曲线

以FPR为横轴，TPR为纵轴，绘制曲线，从阈值为1开始画点，直到阈值为0。将不同阈值下的（FPR，TPR）点连接起来，形成ROC曲线。

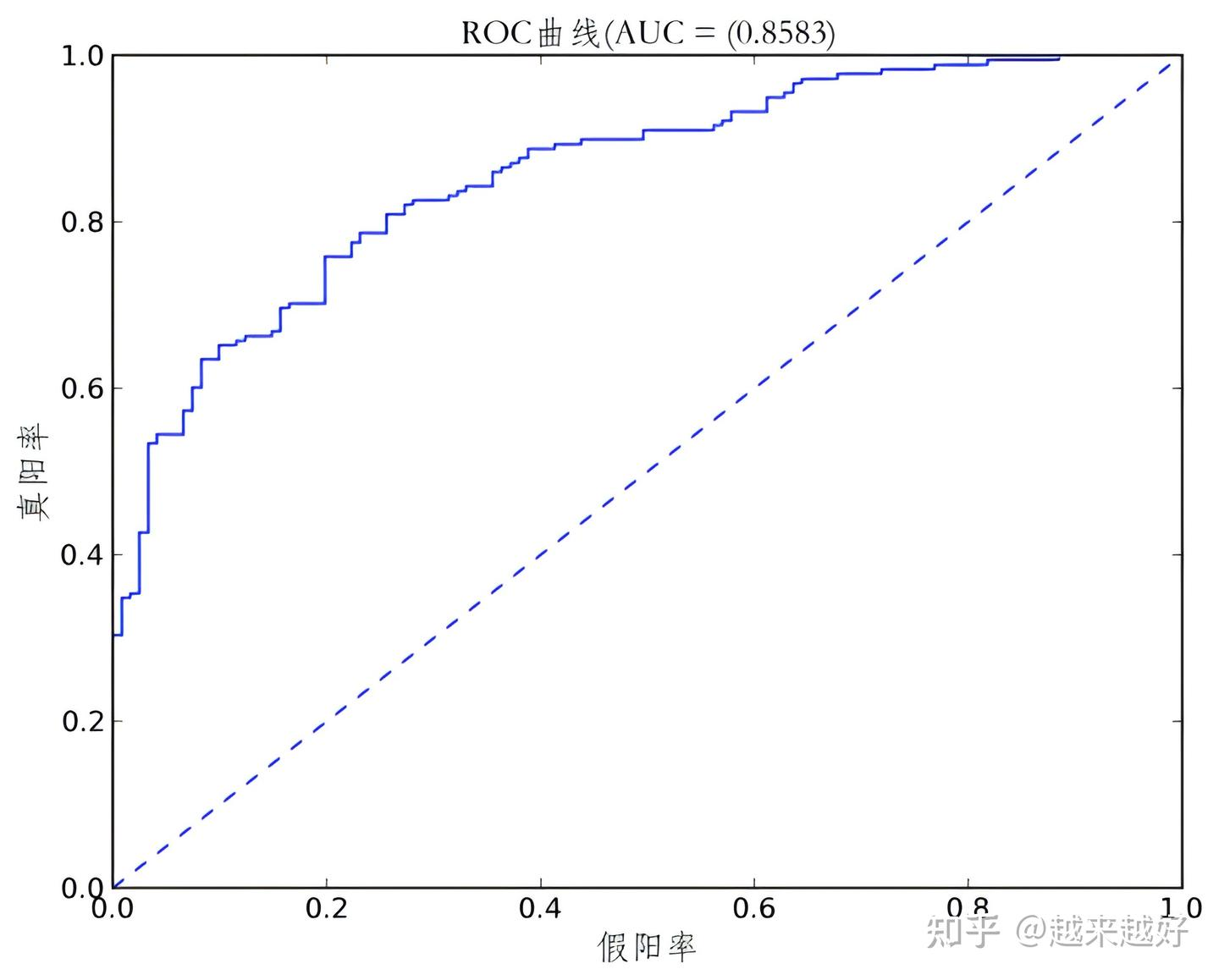
起点（0,0）表示阈值取最大值，所有样本都被预测为负类。终点（1,1）表示阈值取最小值，所有样本都被预测为正类。

随机猜测模型：对角线（从(0,0)到(1,1)的直线），这表示模型没有任何预测能力，TPR与FPR成正比。

完美模型：从(0,0)出发，垂直上升到(0,1)，然后水平向右到(1,1)。这表示模型可以完美地区分正负类，没有任何误判。

实际模型：ROC曲线位于随机猜测模型和完美模型之间，曲线越靠近左上角，模型性能越好。

AUC

AUC（Area Under the Curve，曲线下面积）通常与ROC曲线一起使用。AUC值表示ROC曲线下方的面积，其数值范围在0.5到1之间，用于衡量模型区分正负类的能力。

AUC值的计算公式

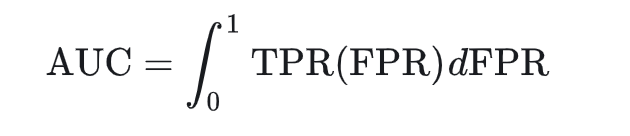
当AUC = 0.5时，模型与随机猜测相当，没有判别能力。当AUC = 1.0时，模型是完美模型，能完全区分正负类。当0.5 < AUC < 1.0时，模型具有一定的区分能力，AUC越大，模型性能越好。

举例：

案例1:

某池塘有1400条鲤鱼，300只虾，300只鳖。现在以捕鲤鱼为目的，撒一大网，逮着了700条鲤鱼，200只虾，100只鳖，那么这些指标如下：
①.正确率：700/(700+200+100)=70%
②.召回率：700/1400=50%
③.F值：2*((70*50)/(70+50))=58.3%

代码

sklearn的精准和找回代码

>>> from sklearn.metrics import precision_score, recall_score
>>> precision_score(y_train_5, y_train_pred) # == 4096 / (4096 + 1522)
0.7290850836596654
>>> recall_score(y_train_5, y_train_pred) # == 4096 / (4096 + 1325)
0.7555801512636044

f1的代码

>>> from sklearn.metrics import f1_score
>>> f1_score(y_train_5, y_train_pred)
0.7420962043663375

案例2

一家电子商务网站希望根据用户的历史行为，向用户推荐他们可能感兴趣的产品。为了评估推荐模型的效果，需要衡量模型在排序时将用户实际感兴趣的产品排在前面的能力。

正样本：用户实际购买或点击的产品。负样本：用户未购买或未点击的产品。

模型为每个产品计算一个预测得分，表示用户对该产品感兴趣的程度。根据预测得分对产品进行降序排序。通过改变得分阈值，计算不同阈值下的TPR和FPR。

正样本（实际感兴趣的产品）：A：0.9、B：0.8、C：0.4

负样本（不感兴趣的产品）：D：0.6、E：0.3、F：0.2

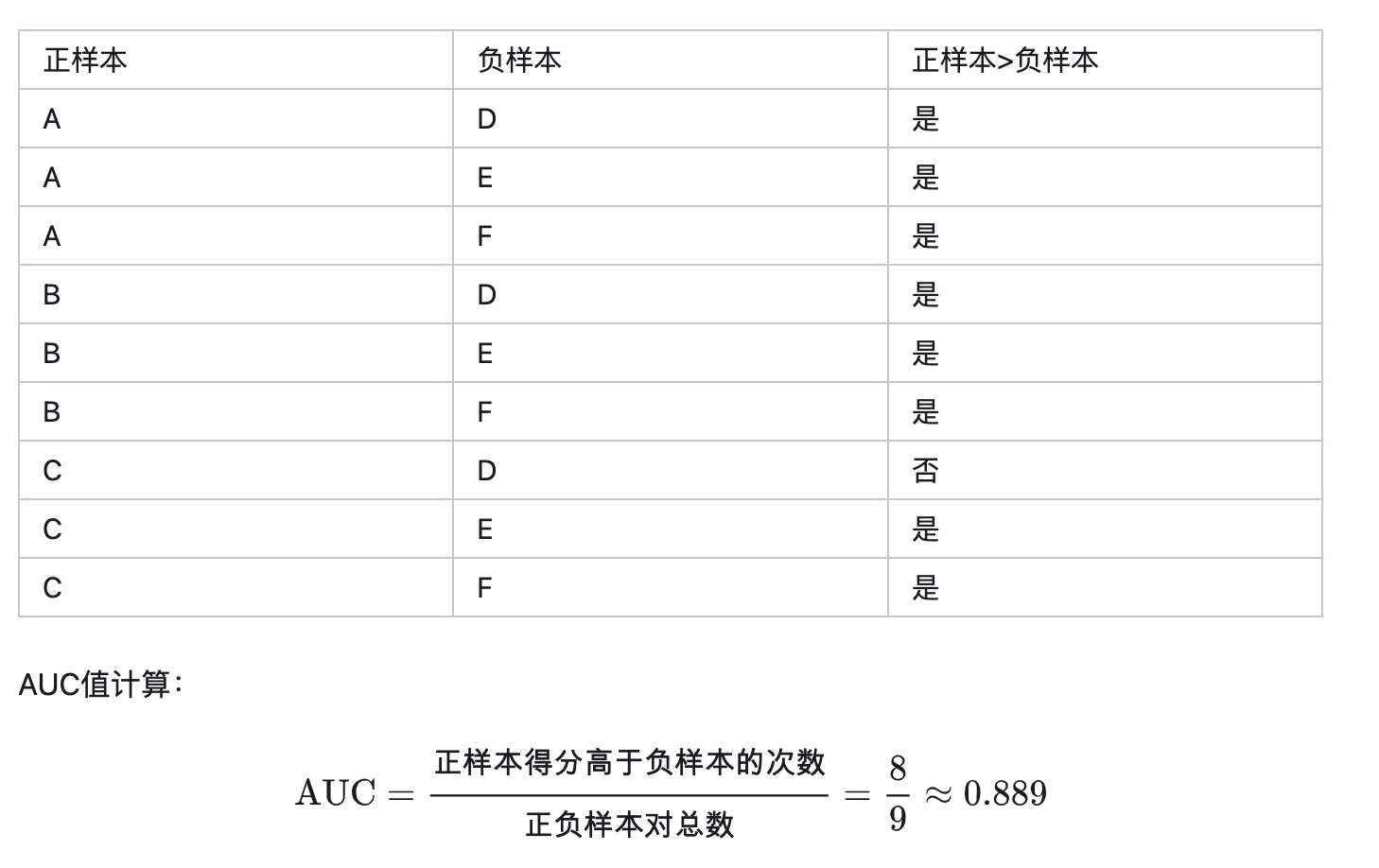
排序结果：A（0.9）、B（0.8）、D（0.6）、C（0.4）、E（0.3）、F（0.2）

分析：在排序结果中，正样本A和B被正确地排在前面，但正样本C被排在负样本D之后。构造所有可能的正负样本对，共有 3×3=9 。

指标对比分析

F1分数对那些具有相近的精度和召回率的分类器更为有利。

这不一定能一直符合你的期望：在某些情况下，你更关心的是精度，而另一些情况下，你可能真正关心的是召回率。

例如，假设你训练一个分类器来检测儿童可以放心观看的视频，那么你可能更青睐那种拦截了很多好视频（低召回率），但是保留下来的视频都是安全（高精度）的分类器，而不是召回率虽高，但是在产品中可能会出现一些非常糟糕的视频的分类器（这种情况下，你甚至可能会添加一个人工流水线来检查分类器选出来的视频）。

反过来说，如果你训练一个分类器通过图像监控来检测小偷：你大概可以接受精度只有30%，但召回率能达到99%（当然，安保人员会收到一些错误的警报，但是几乎所有的窃贼都在劫难逃）。遗憾的是，鱼和熊掌不可兼得，你不能同时增加精度又减少召回率，反之亦然。这称为精度/召回率权衡。

由于ROC曲线与精度/召回率（PR）曲线非常相似，因此你可能会问如何决定使用哪种曲线。有一个经验法则是，当正类非常少见或者你更关注假正类而不是假负类时，应该选择PR曲线，反之则是ROC曲线。

参考文章：

机器学习评估分类结果——精准率、召回率、F1Score_f1 score-优快云博客

第三章.逻辑回归—正确率/召回率/F1指标，非线性逻辑回归代码_正确率召回率-优快云博客

https://zhuanlan.zhihu.com/p/581927291

AUC的三种计算方法及代码_auc计算-优快云博客

蜥蜴书：机器学习实战