String painter HDU - 2476
There are two strings A and B with equal length. Both strings are made up of lower case letters. Now you have a powerful string painter. With the help of the painter, you can change a segment of characters of a string to any other character you want. That is, after using the painter, the segment is made up of only one kind of character. Now your task is to change A to B using string painter. What’s the minimum number of operations?
Input
Input contains multiple cases. Each case consists of two lines:
The first line contains string A.
The second line contains string B.
The length of both strings will not be greater than 100.
Output
A single line contains one integer representing the answer.
Sample Input
zzzzzfzzzzz
abcdefedcba
abababababab
cdcdcdcdcdcd
Sample Output
6
7
题意:
给出两个字符串s1,s2,将s1串变为s2串,每次可以将连续的一个子串改成任意的一个字母,问最少需要操作多少次。
分析:
依最简单的思路,我们定义ans[i]ans[i]代表区间[1−i][1−i]处,A变成B所需要的最小次数,那么转移方程有以下两种情况
1)如果A[i]==B[i]A[i]==B[i]:那么i位置就不需要进行任何操作了,因为它们两个已经相等了,那么此时的状态转移方程 ans[i]=min(ans[i],ans[i−1])ans[i]=min(ans[i],ans[i−1])
当然了如果i是0的时候就是0,因为没有ans[−1]ans[−1]
2)如果i位置不同的话,那么毫无疑问i位置会被刷掉,那么我们假设实际刷的区间是从k−ik−i,即区间[k,i][k,i],就是相当于把A[k,i]A[k,i]这段刷成B[k,i]B[k,i],那么我们发现其实原本的A[k,i]A[k,i]这段字符对我们要求的答案毫无影响,其实就相当于直接把空白串变成B[k,i]B[k,i]。
假设由空白串变成B[k,i]B[k,i]串的最小次数用dp[k][i]dp[k][i]表示
那么此时的状态转移方程为 ans[i]=min(ans[i],ans[k−1]+dp[k][i])ans[i]=min(ans[i],ans[k−1]+dp[k][i])
所以现在的目标是求出由空白串转变成B串需要的最小次数
即求dp[i][j]dp[i][j]
1)最坏的情况下,是将每个字符都变一下,dp[i][i]=1;区间[i,i+1]是由[i,i]扩展来的,dp[i][i+1]=dp[i][i]+1;dp[i][i]=1;区间[i,i+1]是由[i,i]扩展来的,dp[i][i+1]=dp[i][i]+1;
同理:dp[i][j]=dp[i][j−1]+1同理:dp[i][j]=dp[i][j−1]+1
2)如果在区间[i,j][i,j]之间有个kk满足
状态转移方程应该为dp[i][j]=min(dp[i][j],dp[i][k−1]+dp[k][j−1])dp[i][j]=min(dp[i][j],dp[i][k−1]+dp[k][j−1])
这一步怎么来的?
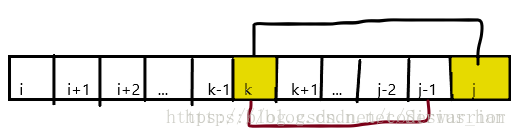
如图所示[i,j]区间可以看作[i,k−1]+[k,j−1][i,j]区间可以看作[i,k−1]+[k,j−1],因为在转化的过程中我们肯定首先先把k位置刷掉,然后在进行k+1k+1之后的位置最后到j位置,但是,因为B[j]==B[k]因为B[j]==B[k],所以我们在刷kk位置的时候完全可以全部刷过去,直接把全都先刷成一种颜色,这样下一步只需要刷[k+1,j−1][k+1,j−1]所以实际上总的来说我们只需要刷区间[k,j−1][k,j−1]即可
因此对于刷区间[i,j][i,j],如果能找到k,jk,j两个位置相同那么只需要将其分成两段,即[i,k−1]和[k,j−1][i,k−1]和[k,j−1]即可
即状态转移方程为:dp[i][j]=min(dp[i][j],dp[i][k−1]+dp[k][j−1])dp[i][j]=min(dp[i][j],dp[i][k−1]+dp[k][j−1])
code:
#include <bits/stdc++.h>
using namespace std;
int main(){
char A[110],B[110];
int dp[110][110],ans[110];
while(~scanf("%s%s",A,B)){
memset(dp,0,sizeof(dp));
int len = strlen(A);
for(int i = 0; i < len; i++) dp[i][i] = 1;
for(int l = 2; l <= len; l++){
for(int i = 0; i + l - 1 < len; i++){
int j = i + l - 1;
dp[i][j] = dp[i][j-1] + 1;
for(int k = i; k < j; k++){
if(B[j] == B[k])
dp[i][j] = min(dp[i][j],dp[i][k-1]+dp[k][j-1]);
}
}
}
for(int i = 0; i < len; i++){
ans[i] = dp[0][i];
if(A[i] == B[i]){
if(i == 0) ans[i] = 0;
else ans[i] = ans[i-1];
}
for(int k = 0; k <= i; k++){
ans[i] = min(ans[i],ans[k]+dp[k+1][i]);
}
}
printf("%d\n",ans[len-1]);
}
return 0;
}




 本文探讨了一种算法问题,即如何将一个字符串通过最少的操作次数转换为另一个字符串。具体而言,每次操作可以将一个子串的所有字符替换为同一个字符,目标是最小化这种替换操作的次数。
本文探讨了一种算法问题,即如何将一个字符串通过最少的操作次数转换为另一个字符串。具体而言,每次操作可以将一个子串的所有字符替换为同一个字符,目标是最小化这种替换操作的次数。
















 641
641

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








