李宏毅机器学习笔记（三）: 梯度下降

一、基本过程

解决一个优化问题，通常需要构造一个 $LossFunction$ ，找到最优的参数 $\theta$ 使 $LossFunction$ 最小：
${\theta }^{\ast }=\underset{\theta }{\mathrm{argmax}}L(\theta ),L:lossfunction\theta :parameters$
假设 $\theta$ 有两个变量 { θ 1 , θ 2 } \{\theta_1,\theta_2\} {θ1​,θ2​}，随机选择始点${\theta }^0=\left[\begin{array}{c}{\theta }_1^0\\ {\theta }_2^0\end{array}\right]$

求偏微分，更新参数，${\theta }^1={\theta }^0-\eta \frac{\partial L({\theta }^0)}{\partial \theta }$

此处减号表示是沿着负梯度方向更新的，梯度是上升最快的方向，负梯度就是下降最快的方向。因为我们要使L达到最小，如果偏导数是正数，说明变量值增加，L变大，此时变量应该减小来使L减小，因此减去$\eta \frac{\partial L({\theta }^0)}{\partial \theta }$；如果偏导数是负数，说明变量值增加，L变小，此时变量应该增加来使L减小，因此减去一个负数$\eta \frac{\partial L({\theta }^0)}{\partial \theta }$

反复迭代得到 ${\theta }^2,{\theta }^3,...$

注：用上标0表示初始的一组参数，下表1和2表示初始的一组参数里面的两个组成(component)

二、一些细节

1. 调整学习率Learning Rate

• 学习率太小：速度会很慢，需要更多次的迭代来达到最小。
• 学习率太大：可能会错过最小点

在一维和二维情况下进行可视化展现，蓝色即学习率过小的情况，绿色即学习率过大的情况：

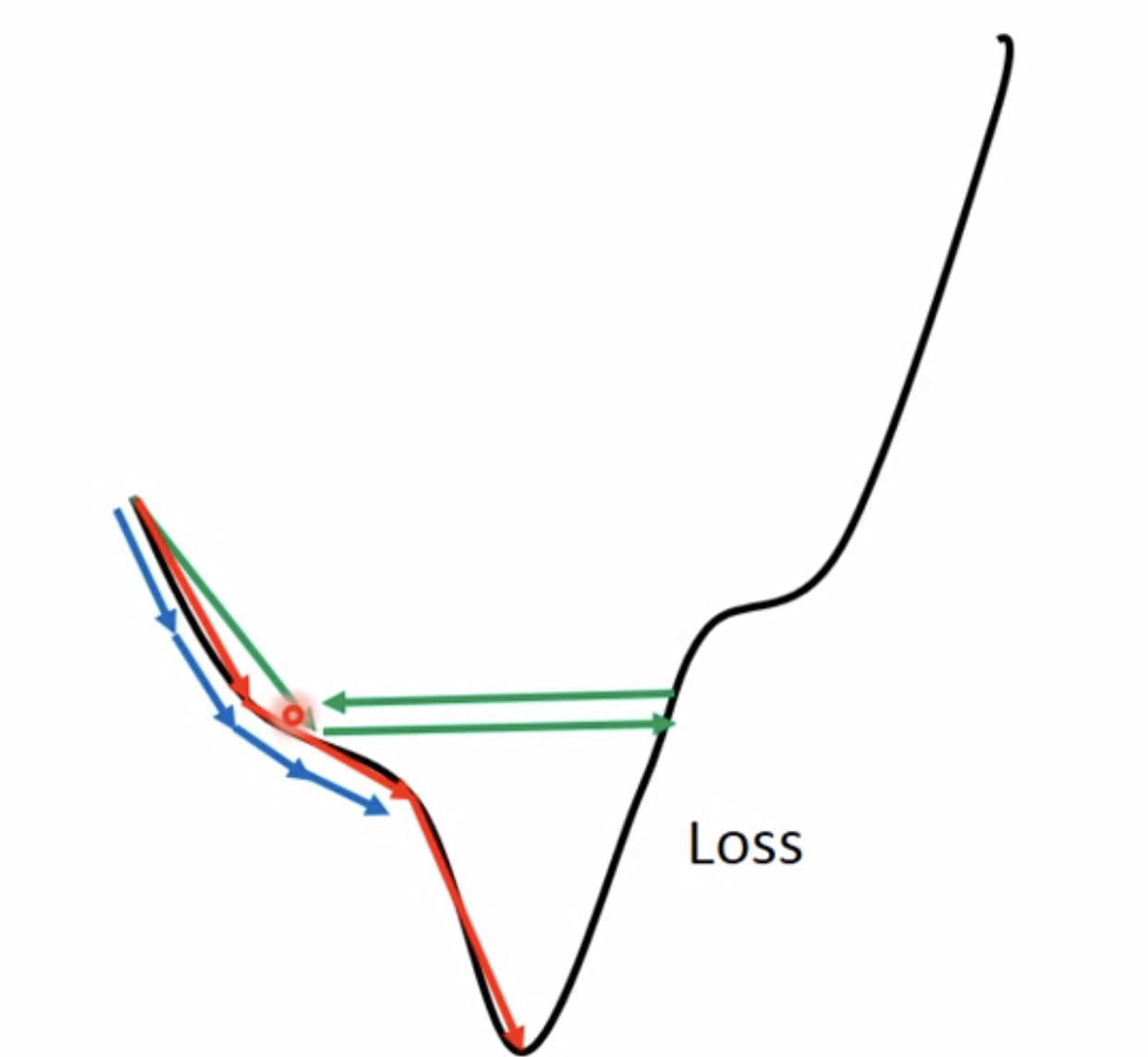
更多维的情况我们是通过对Loss Function的可视化进行观察：

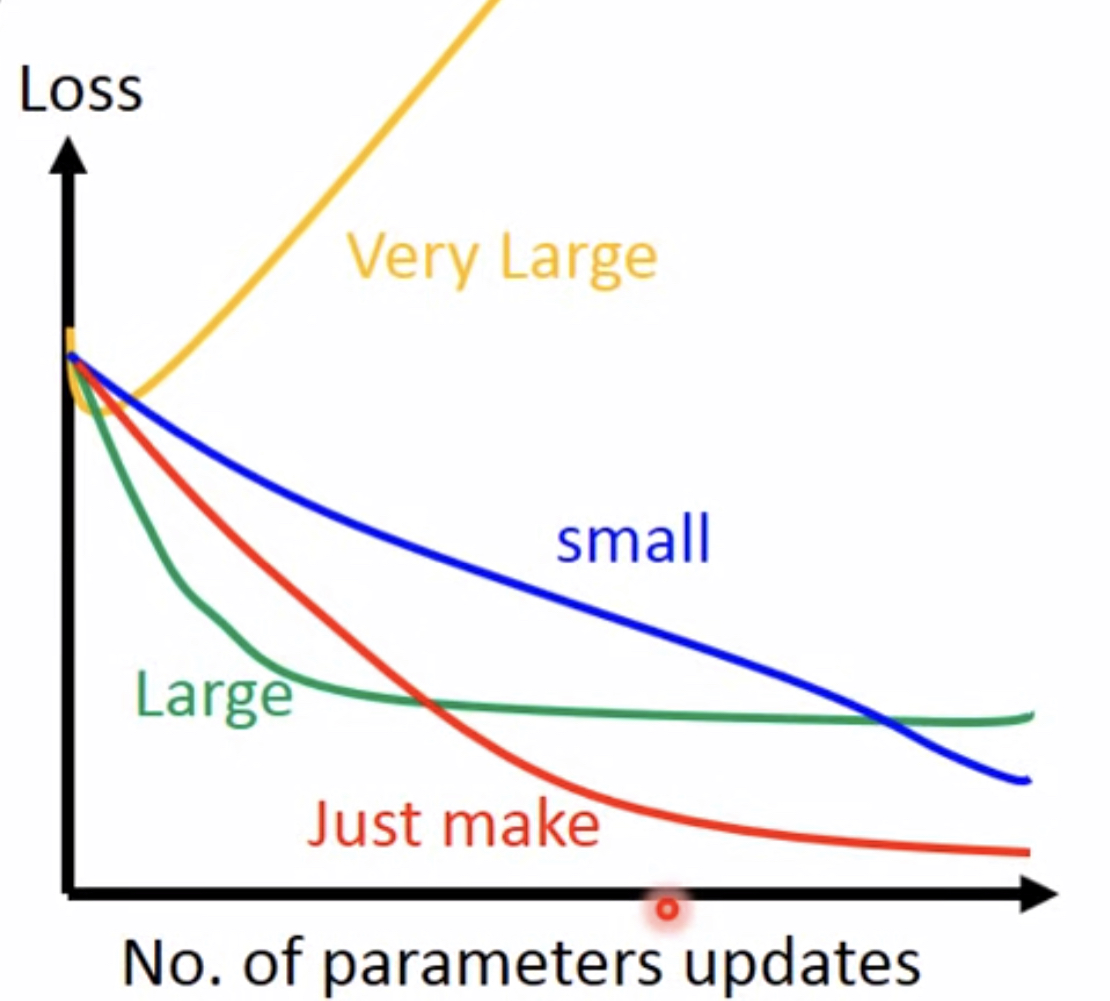
学习率的调参原则 ：学习率随着参数更新越来越小（自适应adaptive）。因为刚开始的时候，离最优点通常是较远的，步伐可以大一点，经过多次迭代后会更加接近目标，所以应当减小学习率防止错过最低点。

● Adagrad自适应梯度算法

每一个参数的学习率都除以之前算出来的微分的均方根（RMS 将所有值平方求和， 求其均值， 再开平方）

• 普通梯度算法 $w^{t+1}\leftarrow w^t-{\eta }^t{g}^t$
• 自适应梯度算法 $w^{t+1}\leftarrow w^t-\frac{{\eta }^t}{{\sigma }^t}{g}^t$

${\sigma }^t：$过去所有的微分值相加求平均值，再开方。例如：

$w^1\leftarrow w^0-\frac{{\eta }^0}{{\sigma }^0}{g}^0$           ${\sigma }^0=\sqrt{(g^0{)}^2}$

$w^2\leftarrow w^1-\frac{{\eta }^1}{{\sigma }^1}{g}^1$           ${\sigma }^1=\sqrt{\frac{1}{2}[(g^0{)}^2+(g^1{)}^2]}$

$......$
$w^{t+1}\leftarrow w^t-\frac{{\eta }^t}{{\sigma }^t}{g}^t$           ${\sigma }^t=\sqrt{\frac{1}{t+1}\sum _{i=0}^t(g^i{)}^2}$

而   ${\eta }^t=\frac{\eta }{\sqrt{t+1}},$

因此， $w^{t+1}\leftarrow w^t-\frac{\eta }{\sqrt{\sum _{i=1}^t(g^i{)}^2}}{g}^t$

观察表达式可以看出，梯度下降的速度和两个因素有关，一个是学习率 $\eta$，在Adagrad中对其进行多一步的处理，另一个是梯度 $g^t$，而在此处出了一个矛盾 ：之前一直说斜率/梯度越大，更新越快，而Adagrad中， $g^t$告诉我们微分值越大，参数更新得越快，而 $\frac{\eta }{\sqrt{\sum _{i=1}^t(g^i{)}^2}}$ 告诉我们微分值越大，更新速度反而小。

有些文章认为：Adagrad是想研究gradient有多反差：How surprise it is？考虑过去每一次的gradient，使之相除，造成反差的效果。

更正式的解释：Larger gradient, larger steps?

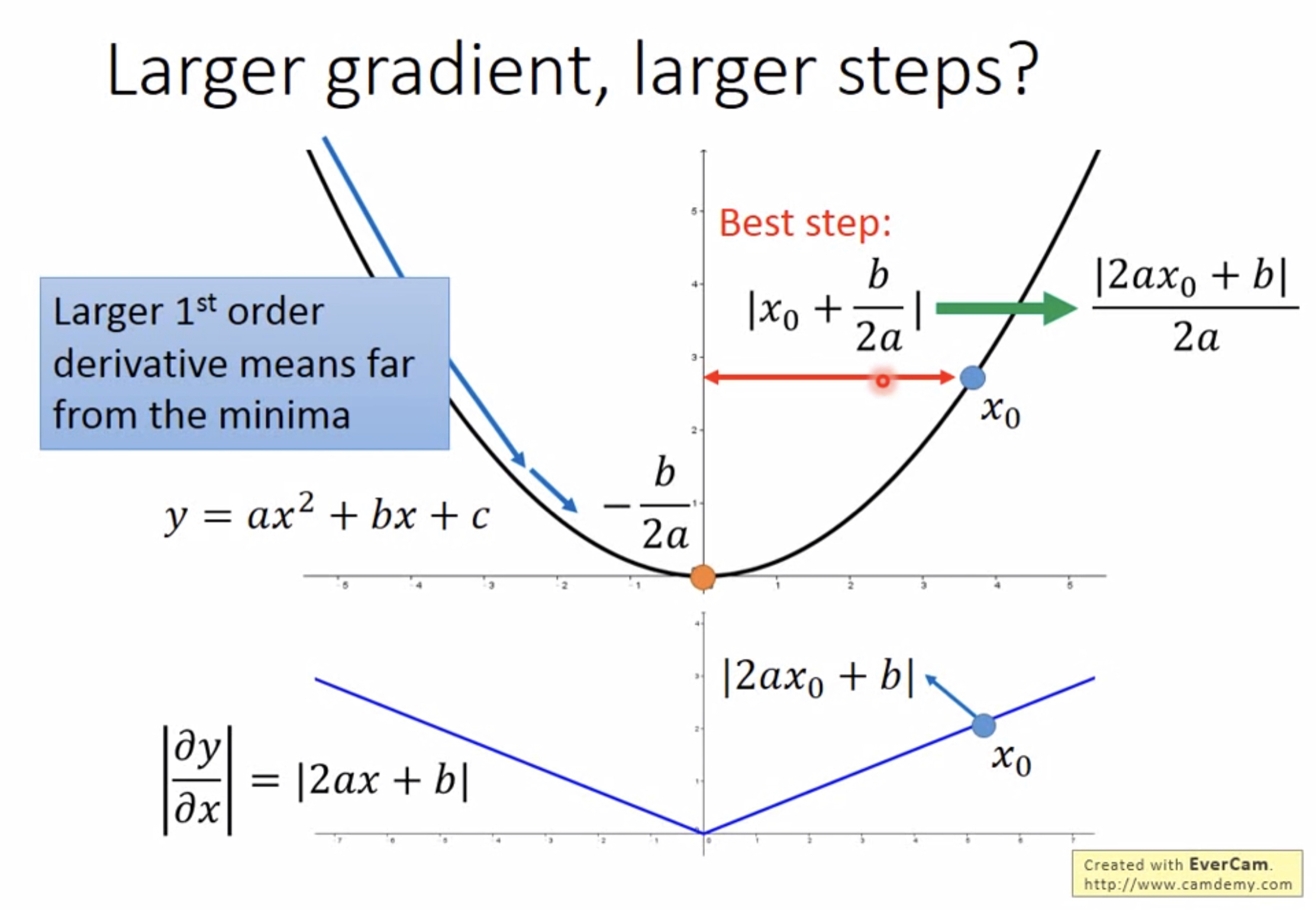
以二次函数为例，其最低点的横坐标是$-\frac{b}{2a}$，任取一个$x_0$，多大的步长能使其到最低点呢？ ——$|x_0+\frac{b}{2a}|=\frac{|2a{x}_0+b|}{2a}$，分子刚好就是一阶导数，注意此处a是大于0的，若微分值越大，也就离最低点越远。 我们想要到达最低点，最好就选取 $\frac{|2a{x}_0+b|}{2a}$为步长。

但是这只有在含一个参数的情况下成立，若有多个参数则不成立。以两个参数的情况为例：

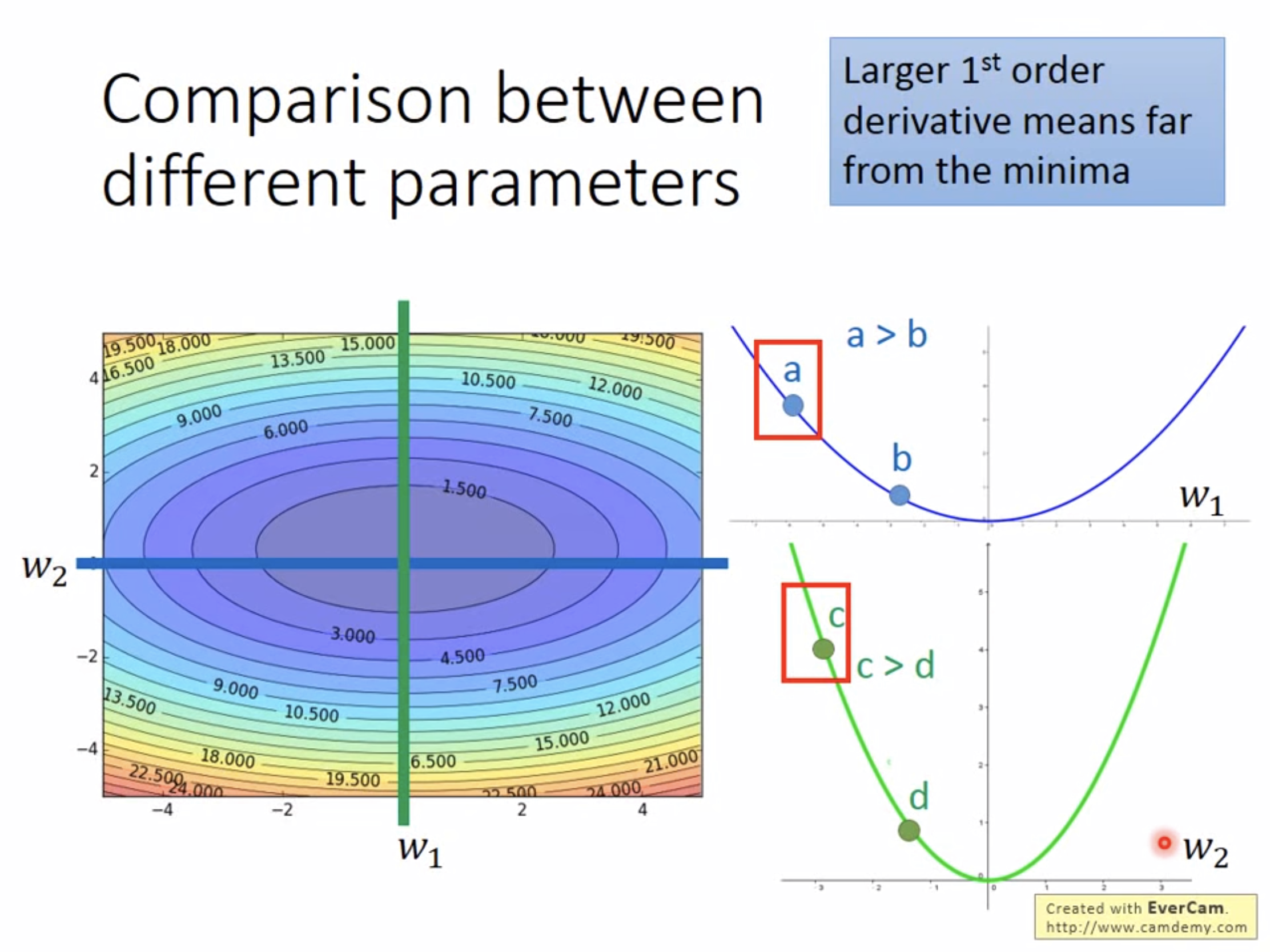
只考虑$w_1$时，a的微分要大于b，a距离最低点也比b更远，这符合前面的描述；
只考虑$w_2$时，c的微分要大于d，c距离最低点也比d更远，这同样符合前面的描述；

但是跨参数比较时就不一定成立，例如a的微分值小于c，但是a可能离最低点更远。所以要进一步改进，这时考虑，$\frac{|2a{x}_0+b|}{2a}$的分子其实就是二次函数的二阶导，应当将二次微分也考虑进来，最佳步长：$\frac{一阶偏微分}{二阶偏微分}$

再回到Adagrad的参数更新表达式 $w^{t+1}\leftarrow w^t-\frac{\eta }{\sqrt{\sum _{i=1}^t(g^i{)}^2}}{g}^t$，$\eta$是个常量

$\frac{g^t}{\sqrt{\sum _{i=1}^t(g^i{)}^2}}$ 分子是一阶微分，分母不是二阶微分，但是事实上是二阶微分的近似，且这样使得计算量小，因为一阶微分是我们本来就需要计算的，现在用这种方式对二阶微分进行近似，不需要进行额外的计算。

2. 更快的参数更新速度

● SGD随机梯度下降法

• 普通梯度下降：$L=\sum _n({\hat{y}}^n-(b+\sum w_i{x}_i^n){)}^2$
• 随机梯度下降：$L^n=({\hat{y}}^n-(b+\sum w_i{x}_i^n){)}^2$

SGD是随机选取一个$x^n$ ，根据参数在该样本中的表现计算Loss，注意SGD的式子中，保留了第二个$\sum$，这是表示对样本$x^n$的所有feature进行计算。

SGD每次根据一个数据进行计算并更新参数，而不是考察所有数据后再更新，这样使得SGD计算速度很快。

与SGD相对的是Batch GD 批量梯度下降，我们一般说的GD就是BGD，将二者进行对比：

	BGD	SGD
所用数据	每一次更新要用到所有数据	每次更新仅用一个数据
梯度方向	更准确的梯度计算方向	梯度下降准确性降低
收敛性	100%能找到全局最优	对于凸函数可能也只找到局部最优
训练时间	训练速度慢	训练速度很快

将二者结合即得到mini-Batch GD（小批量梯度下降），每次选取一定量的数据进行参数更新，相比BGD可以降低时间花费，相比SGD更加准确。

3. Feature Scaling特征归一化

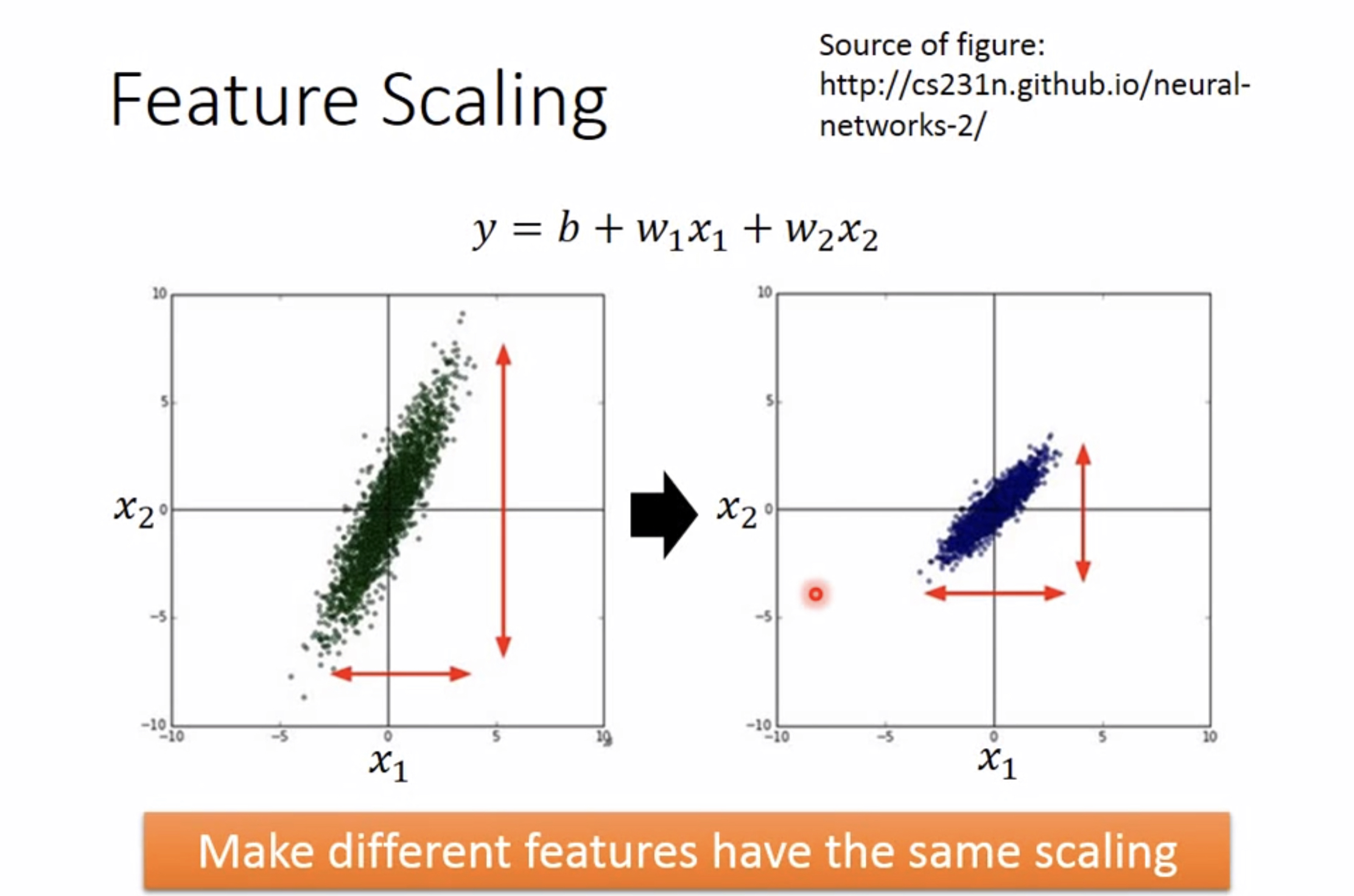
为什么？

• 特征间的单位（尺度）可能不同，比如身高和体重，比如摄氏度和华氏度，比如房屋面积和房间数，一个特征的变化范围可能是[1000,10000]，另一个特征的变化范围可能是[−0.1,0.2]，在进行距离有关的计算时，单位的不同会导致计算结果的不同，尺度大的特征会起决定性作用，而尺度小的特征其作用可能会被忽略，为了消除特征间单位和尺度差异的影响，以对每维特征同等看待，需要对特征进行归一化。
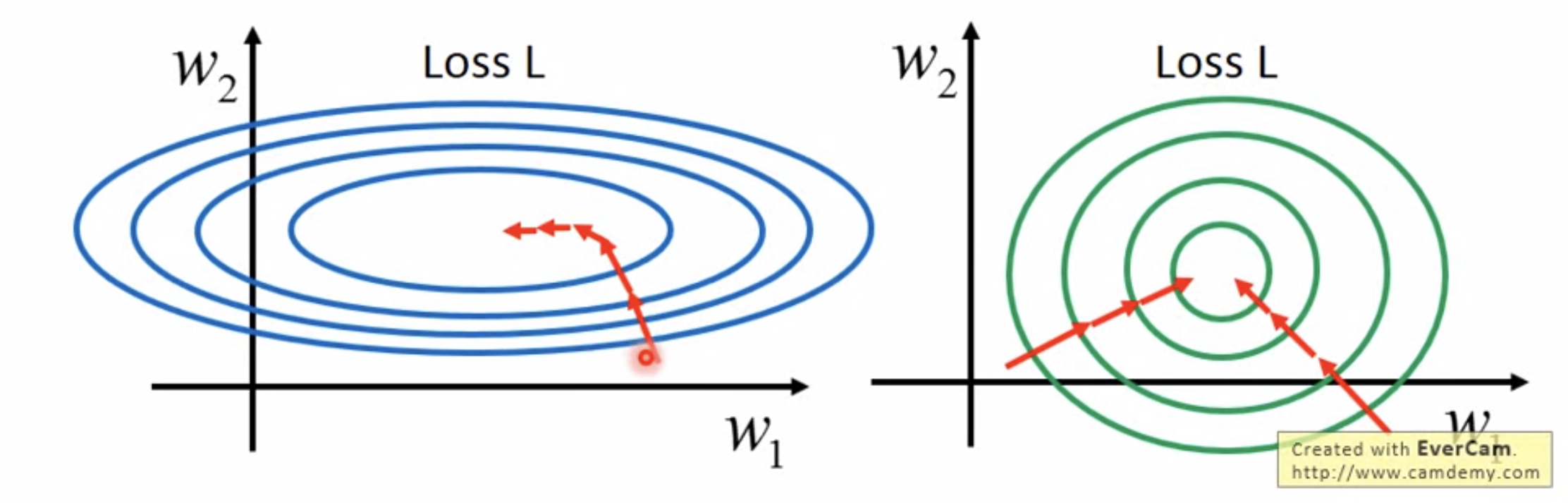
• 原始特征下，因尺度差异，其损失函数的等高线图可能是椭圆形，梯度方向垂直于等高线，下降会走zigzag路线，而不是指向local minimum。通过对特征进行zero-mean and unit-variance变换后，其损失函数的等高线图更接近圆形，梯度下降的方向震荡更小，收敛更快。
  ——来自为什么要归一化？

怎么做？
归一化方法有很多，最常用的是z-score法 和min-max法。

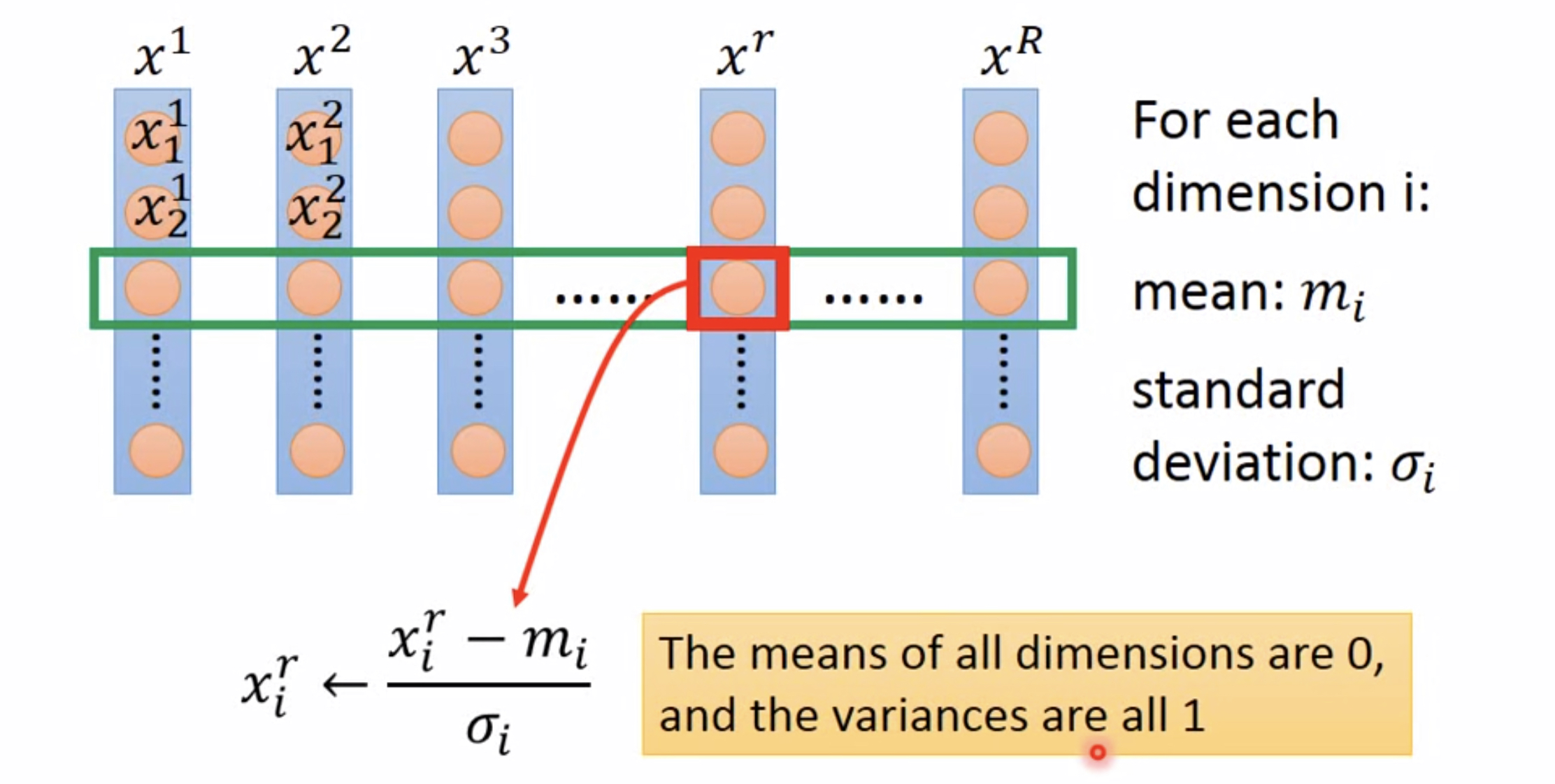
上图所示为z-score方法的思想，注意归一化是对每一个属性分别归一化，对于一个属性，计算其取值的出平均值和方差，归一化后的属性值为$\frac{x-\mu }{\sigma }$，在实际应用中，是否归一化会对结果产生较大的影响，一般我们都会在数据预处理阶段进行归一化操作。

三、梯度下降的局限性

对于非凸函数，并不一定能找到全局最优。