服务器辅助的PEKS方案

原创于 2025-10-21 09:24:36 发布 · 779 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#SA-PEKS # 关键词猜测攻击 # 盲签名 # 限速机制

服务器辅助的基于关键词搜索的公钥加密

摘要

基于关键词搜索的公钥加密（PEKS）是一种在云存储中实现安全可搜索数据加密的著名密码学原语。然而，它本质上容易受到（内部）离线关键词猜测攻击（KGA）的影响，从而威胁用户的数据隐私。现有的应对措施主要存在效率低下的问题，难以在实际应用中广泛使用。在本研究中，我们通过形式化一种新的PEKS系统——服务器辅助的带关键字搜索的公钥加密（SA‐PEKS），为这一安全漏洞提供了实用且可行的解决方案。在SA‐PEKS中，用户需要通过运行一个认证协议向一个称为关键词服务器（KS）的半可信第三方发起查询，以生成关键词密文或陷门，从而实现抵御离线KGA的安全性。接着，我们提出了一种通用转换方法，利用确定性盲签名将任意PEKS方案转换为安全的SA‐PEKS方案。为了验证其可行性，我们通过采用FDH‐RSA签名以及Boneh等人在Eurocrypt2004上提出的PEKS方案，给出了首个SA‐PEKS方案的实例化。最后，我们描述了如何结合限速机制安全地实现客户端‐KS协议以抵抗在线KGA，并通过实验评估了我们方案的性能。

引言

L oud存储外包近年来受到企业和组织越来越多的关注，以减轻维护大数据的负担。实际上，终端用户可能更倾向于加密其外包数据以保护隐私，因为他们可能并不完全信任云存储服务器。这使得传统数据利用服务（如对文本数据的明文关键词搜索或对数据库的查询）难以部署。其中一种典型解决方案是可搜索加密，它允许用户搜索和检索加密数据，同时保护数据隐私。可搜索加密可以在对称[1],[2]或非对称加密环境[3],[4]下实现。对称可搜索加密（SSE）由Song 等[1]提出，并由Curtmola等[2]进行了形式化研究。尽管 SSE方案效率较高，但存在复杂的密钥分发问题。公钥环境下的可搜索加密源于存储转发系统，例如电子邮件系统，其中接收者可以搜索数据由Bonehet al.[3]首次提出，在外包存储系统中基于接收者的公钥对数据进行加密。他们首次引入了一种更为灵活的原语，即基于关键词搜索的公钥加密（PEKS），使用户能够在非对称加密环境中搜索加密数据。在PEKS系统中，发送者使用接收者的公钥将一些加密关键词（称为PEKS密文）与加密数据关联。然后，接收者向服务器发送待搜索关键词的陷门以进行数据检索。服务器利用该陷门和PEKS密文，通过Test操作判断PEKS密文所隐藏的关键词是否与接收者选定的关键词相等。若是，则服务器将匹配的加密数据发送给接收者。

本工作的动机

不幸的是，尽管PEKS方案无需分发私钥，但其在关键词隐私方面存在一种固有的安全问题，即（内部）离线关键词猜测攻击（KGA）。具体而言，给定一个陷门后，恶意服务器可以从关键词空间中选择一个猜测关键词，并利用该关键词生成PEKS密文，然后通过测试判断该猜测关键词是否为陷门所对应的关键词。这种猜测-然后测试的过程可以不断重复，直到找到正确的关键词。由于关键词往往可能泄露用户数据的一些敏感信息，因此克服这一安全威胁对于实现安全且可搜索的加密数据外包具有重要的实际意义。

在[5],彭等人提出了一种带模糊关键词搜索的公钥加密（PEFKS）概念，其中每个关键词对应一个精确陷门和一个模糊陷门。服务器仅被提供模糊陷门，因此无法获知确切的关键词。然而，在他们的方案中，恶意服务器仍然能够识别出底层关键词所属的一个小集合，从而导致服务器无法很好地保护关键词隐私。另一方面，该方案并不实用，因为接收者必须使用精确陷门对服务器返回的集合进行本地筛选，以找出匹配的密文。

Chen等人[6],[7]提出的另一项工作引入了一种新的 PEKS框架，即双服务器基于关键词搜索的公钥加密（ DS‐PEKS），以实现抵御内部关键词猜测攻击的安全性。他们的核心思想是通过将PEKS系统的测试功能拆分为两部分，并由两个独立的服务器分别处理，从而禁止对PEKS的独立测试。因此，只要两个服务器不共谋，就能实现抵御离线 KGA的安全性。然而，双服务器PEKS可能仍存在效率低下的问题，因为关键词搜索现在需要由两个服务器分别处理。

在本研究中，我们旨在设计一种更为实用的方法来解决这一安全性问题。此外，我们希望构建一个能与任何现有 PEKS系统透明协作的系统。也就是说，该系统将具有向后兼容性，并且不会对底层PEKS系统的实现细节进行任何修改。

我们的贡献

本文的贡献主要有四个方面。首先，我们形式化了一种新的PEKS系统，名为基于关键词搜索的服务器辅助公钥加密（SA‐PEKS），以应对现有PEKS系统中针对（内部）离线KGA的安全漏洞。我们提出的解决方案能够与任何现有的PEKS系统透明地协同工作，因此在实际应用中更具可行性。其次，我们提出了SA‐PEKS方案的通用构造，并进行了形式化安全分析。具体而言，我们提出了一种通过利用确定性盲签名将任意PEKS方案转换为SA‐PEKS方案的通用方法。第三，为了说明所提出的通用转换的可行性，本文给出了SA‐PEKS方案的一个实例化。我们基于F DH‐RSA盲签名和Boneh等人提出的PEKS方案[3]对该方案进行了实例化。最后，我们实现了所提出的方案，并通过实验分析了其性能。特别是，我们展示了如何结合限速机制安全地实现客户端‐KS协议以抵御在线KGA。

服务器辅助的PEKS

概述

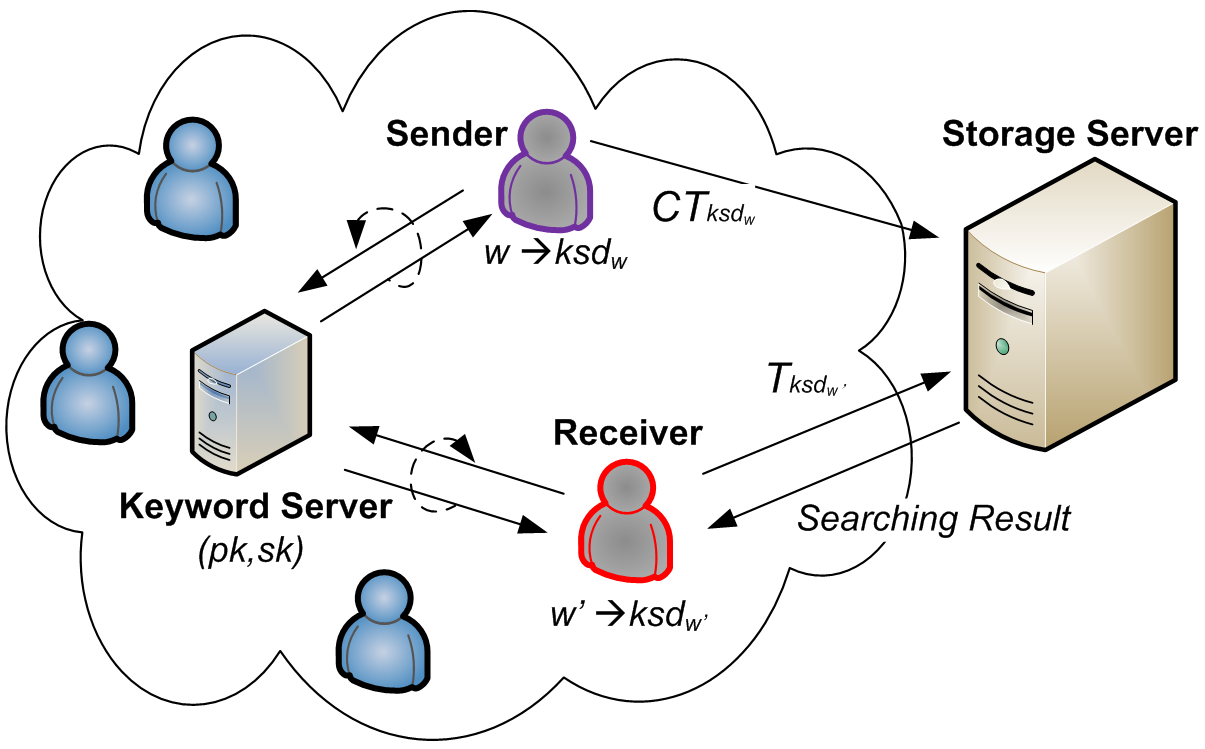
SA‐PEKS的提出基于以下观察：通过引入一个半可信的第三方，即与存储服务器（SS）分离的关键词服务器（KS），可以应对离线KGA，如图1所示。大致而言，在SA‐PEKS系统中，KS拥有公钥/私钥对（pk, sk）。用户向KS进行身份认证，并被分配特定于用户的凭据。与直接从原始关键词生成 PEKS密文和陷门的PEKS框架不同，用户在生成PEKS密文和陷门前，需要以经过认证的方式与KS交互，获取预处理后的关键词，即KS派生关键词。具体来说，给定一个原始关键词 w，发送方必须通过认证访问KS，并与KS运行一个交互协议。在协议执行结束时，发送方获得对应 w的KS派生关键词为 ksdw。随后，发送方将该KS派生关键词 ksdw视为最终关键词来生成PEKS密文。类似地，接收者输入指定关键词 w′，与KS运行交互协议以获得KS派生关键词 ksdw ′，然后生成相应的陷门。要求从原始关键词到KS派生关键词的派生算法必须是确定性的，否则SA‐PEKS无法正确工作。也就是说，如果 w= w ′，则有 ksd w = ksd w ′。可以看出，这种方式使得PEKS密文和陷门的生成转变为在线方式进行（通过协议），从而实现抵御离线KGA的安全性。

形式化定义

定义4（服务器辅助的PEKS） 。一个SA-PEKS方案由六元组(SA-KeyGenKS, SA-KeyGenR,SA-KSD, SA-PEKS,SA-Trapdoor,SA-Test)定义如下。

SA-KeyGenKS(λ) 。输入安全参数 λ，输出密钥服务器的公钥/私钥对为(pkks, skks)。
SA-KeyGenR(λ) 。输入参数 λ，输出接收者的公钥/私钥对为(pkR, skR)。
SA-KSD(pkks, skks, w) .输入密钥服务器的密钥对和关键词 w，返回KS派生关键词 ksdw。
SA-PEKS(pkR, ksdw) .输入接收者的公钥 pkR和KS派生关键词 ksdw，发送者输出关键字 w的PEKS密文 w为 CTksdw。
SA-陷门(skR,ksdw′) 。输入密钥 skR 接收者和KS派生关键词ksdw′，接收者输出陷门为 Tksdw′。
SA-Test(pkR, CTksdw, Tksdw′) 。输入公钥 pkR，PEKS密文 CTksdw 和陷门 Tksdw′ 存储服务器输出 T rue如果 w= w′；否则输出 F alse。

正确性 。要求对于任意两个关键词 w, w′, ksdw ← SA‐KSD(pkks, skks, w) ksdw′ ←SA‐KSD(pkks, skks, w ′) CTksdw ← SA‐PEKS(pkR, ksdw)以及 Tksd w ′ ← SA‐Trapdoor(skR, ksdw′)，当 w= w′时，有SA‐Test(pkR, CTksdw , Tksd w ′)= T rue。

备注1 . 算法SA‐KSD是用户（发送方/接收者）与密钥服务器之间的一个交互协议。密钥服务器和用户均以公开信息 pkks 作为输入，密钥服务器的私有输入为 skks，而用户的私有输入为原始关键词。密钥服务器和用户执行KS派生关键词签发协议，并在多项式时间内结束。当协议完成后，用户的私有输出包含KS派生关键词。不失一般性，我们假设用户能够利用公开信息验证KS派生关键词的有效性，因此算法 SA‐KSD在交互协议成功完成后总是输出密钥服务器导出的关键词。

安全模型

在本小节中，我们将分别针对对抗性存储服务器、诚实但好奇的密钥服务器以及对抗性用户，定义SA‐PEKS的安全模型。

对抗性存储服务器（SS）

在此，我们提出了一种新的概念，即针对SA‐PEKS的选择关键词猜测攻击下的语义安全性（ SS‐CKGA）。与PEKS中的SS‐CKA概念类似，SS‐CKGA保证SA‐PEKS中的PEKS密文不会泄露底层关键词的任何信息。 SS‐CKGA与SS‐CKA之间的区别在于，针对SA‐PEKS的对手被允许获得挑战PEKS密文的匹配陷门。

定义5（SS‐CKGA） 。 SS-CKGA游戏如下。

设置 .挑战者生成密钥对(pkR , sk R )、(pkks , sk ks )，并将(pkR , pkks )发送给攻击者。
查询-I 。攻击者可以自适应查询挑战者关于任意关键词的陷门和 PEKS密文。
挑战。攻击者向挑战者发送两个关键词w0, w1。此处的限制是，在查询-I中既没有查询过 w0，也没有查询过 w1。挑战者随机选择 b←${0, 1}，并生成 ksdwb←SA-KSD(pkks, skks, wb)， CT ∗←SA-PEKS(pkR, ksdwb) T ∗←SA-Trapdoor(skR, ksdwb)。然后，挑战者将(CT ∗, T ∗)发送给攻击者。事件Q
查询-II . Th攻击 k攻击者可以继续 h查询 f or th陷门 door 以及其选择的任意关键词（除了挑战者C ge key关键字w w0, w1。
输出 .最后，攻击者输出其对 b′ ∈{0, 1}的猜测 b，如果 b= b′则赢得游戏。

我们称上述游戏中的此类对手 A为SS‐CKGA对手，并将其优势定义为AdvSS CKGA SS A-,(λ)= Pr[b= b′] − 1/2.

诚实但好奇的关键词服务器（KS）

要求该协议不能向KS 或其他外部攻击者泄露用户的私有输入的任何信息。形式上，我们定义了选择关键词攻击下的不可区分性（IND‐CKA），如下所示。

定义6（IND‐CKA） 。 IND-CKA游戏定义如下，

设置 .挑战者运行算法密钥生成算法(λ) 并将公钥/私钥对 (pkks, skks) 发送给攻击者。随后，攻击者向挑战者发送两个关键词 w0, w1。
挑战。挑战者选取 b←${0, 1}，并以关键词 wb作为输入，与攻击者运行基于KS的关键词生成协议。
输出 .协议执行完成后，攻击者输出其对 b′ ∈{0, 1}的猜测 b，如果 b= b′成立，则赢得游戏。

我们称上述游戏中的此类对手 A为IND‐CKA对抗者，并将其优势定义为AdvIND CKA KS A-,(λ)= Pr[b= b′] − 1/2.

对抗性用户

要求只有密钥服务器（KS）才能生成正确的 KS派生关键词，否则SA‐PEKS的安全性退化为原始PEKS的安全性，即无法抵御离线关键词猜测攻击。此外，我们还应防止对抗性用户根据从KS获取的先前KS派生关键词生成新的KS派生关键词。因此，为了最好地体现这一安全要求，我们定义了如下所述的选择关键词攻击下的单次多关键词不可伪造性（OMU‐CKA）。

定义7（OMU‐CKA） 。 OMU-CKA游戏定义如下，

设置 .挑战者运行算法密钥生成算法(λ) 以获得密钥对 (pkks, skks)。攻击者被给予 pkks。
KSD-查询 。攻击者可以自适应查询挑战者对于KS派生关键词，最多对应 qk个不同的原始他选择的关键词 w1, w2,…, w q k 通过该协议。
输出 .最后，攻击者输出qk + 1对 {wi , ksd w i }i ∈[ 1, q k +1 ] 并赢得游戏，如果 (1) wi 6 = w j ，对于任意 i, j ∈[1, qk + 1]，其中 i 6= j，且 (2) ksdwi 是有效的任意 i ∈[1, qk +1]的 w i的KS派生关键词。

我们将上述游戏中的此类对手 A称为OMU‐CKA对手，并将其优势Adv OMU CKA U ‐,(λ)定义为对手A在上述游戏中获胜的概率。

基于上述定义的安全模型，我们给出SA‐PEKS方案的以下安全定义。

定义8（安全的SA‐PEKS） 。我们称一个SA‐PEKS是安全的，如果对于任意多项式时间攻击者 A i

3 PEKS到SA‐PEKS的通用转换

3.1 盲签名

在介绍通用转换之前，我们简要回顾一下盲签名的定义。盲签名由Chaum[17]提出。

语法。形式上，一个盲签名方案是一个由算法元组(Kg, Sign,User,Vf)构成的交互式方案。假设系统安全参数为 λ。签名者通过密钥生成算法(pk, sk)←$ Kg(λ)生成密钥对。为了获得对消息 m ∈{0, 1}∗的签名，用户和签名者根据算法 User(pk, m)和Sign(sk)执行交互式签名协议。协议完成后， User算法本地输出关于 m的签名 σm 。为了验证签名 σm的有效性，验证算法Vf以 pk, m和 σm作为输入，若签名有效则输出 T rue，否则输出 False。如果对于任意 (pk, sk) ←$ Kg(λ)、任意消息 m 以及在与Sign(sk)交互后由User(pk, m)输出的任意签名 σm，均有Vf(pk, m, σm) = True，则该盲签名方案具有正确性。

如果对于每个公钥pk和每条消息 m，都仅存在一个签名 σm，使得Vf(pk, m, σ)= T rue成立，则该盲签名是确定性的。

安全性 。盲签名的安全性包含两个方面：不可伪造性和盲性。我们称一个盲签名方案是一更多不可伪造的，如果任何多项式时间对手在向签名预言机查询 qs个不同消息的情况下，仅能以可忽略的概率伪造出 qs+1个有效消息/签名对。另一个概念即盲性，要求签名者无法分辨其正在签名的消息。更准确地说，盲性条件要求恶意签名者在与诚实用户的两次执行过程中，无法判断两个消息中哪一个被首先签名。

3.2 一种通用转换

在本小节中，我们展示了一种从PEKS到SA‐PEKS的通用转换。给定一个确定性盲签名方案 BS=(Kg, Sign,User, Vf) 和一个PEKS方案PEKS=(KeyGen, PEKS,Trapdoor, Test)，所得到的SA‐̂PEKS方案如下。令 H:{0, 1} ∗ ×{0, 1} ∗ → {0, 1} ∗为一个密码学抗碰撞性哈希函数。

SA‐密钥生成算法KS(λ) 。输入安全参数 λ，并通过运行输出KS的公钥/私钥对将算法Kg的 BS 表示为(pkks , sk ks) ←$ Kg(λ)。
SA‐密钥生成算法R(λ) 。输入参数 λ，并通过运行 PEKS的密钥生成算法输出接收者的密钥对，即(pkR , sk R) $ ←密钥生成算法(λ)。
SA‐KSD(pkks , sk ks , w) 。输入KS的密钥对和关键词 w，用户（发送方/接收方）运行算法User(pkks , w)，KS在交互式签名协议中运行 BS的算法Sign(skks) ，以获得 w的有效签名 σ w 。用户最终获得KS派生关键词为 ksd w = H(w, σ w)。
SA‐PEKS(pkR, ksdw) 。输入公钥pkR和KS派生关键词 ksdw，发送方执行 PEKS的算法PEKS ，即 CTksdw ←PEKS(pkR, ksdw)。然后输出 CTksdw作为 w的PEKS密文。
SA‐陷门(skR,ksdw′) 。输入接收者的私钥 skR和KS派生关键词ksdw′，接收者运行 PEKS的算法Trapdoor，即 Tksdw′ ← Trapdoor(skR,ksdw′)。然后输出 Tksdw′作为 w′的陷门。
SA‐Test(pkR, CTksdw, Tksdw′) 。输入公钥pkR、PEKS密文 CTksdw和陷门Tksdw′，存储服务器SS执行 PEKS的 Test算法，即T rue/F alse← PEKS(pkR, CTksdw, Tksdw′)。然后输出 True/F alse作为测试结果。

正确性分析 。可以看出，该构造的正确性条件成立是由于抗碰撞̂哈希函数 H、确定性的方案 BS以及 PEKS的正确性。更准确地说，对于任意关键词w, w′，我们有 σw= σ′ w ，因此当 w= w′时，有 ksdw= ksdw′；否则，我们有 ksdw 6= ksdw′。因此，由于 PEKS的正确性，当 w= w′时，有T rue← PEKS(pkR, CTksdw, Tksdw′)；否则， F alse← PEKS(pkR, CTksdw, Tksdw′)。

3.3 安全分析

SS‐CKGA安全性 。形式上，上述SA‐PEKS方案 SA‐ PEKS的SS‐CKGA安全性由以下定理保证。

定理1 。设哈希函数 H为一个随机预言机。假设存在一个多项式时间敌手 A能够以优势AdvSS CKGA SS A-,攻破上述方案 SA-PEKS的SS-CKGA安全性，则存在一个多项式时间敌手 B ，能够以至少为Adv OMU BS,B ≥ 1/qĤ · AdvSS CKGA SS A-,的优势攻破底层签名方案 BS的多一不可伪造性，其中qĤ是̂对 H 的查询次数。

证明：我们通过构造一个算法 B来证明该定理，该算法在SS‐CKGA模型中模拟挑战者与 A进行游戏。 B的目标是攻破方案 BS的一更多不可伪造性安全性。假设 B获得了 BS的公钥 pkks，然后 B按如下方式与 A交互。

在设置阶段， B运行密钥生成算法KeyGen以生成密钥对(pkR, skR)，并将 pkR,pkks发送给对手 A。在查询I阶段，当 A针对PEKS密文（或陷门）查询关键词 w时， B首先与签名预言机交互以获取 w ̂ 的签名，并访问随机预言机 H以获得由KS导出的关键词 ksd w。然后 B 使用(pkR, skR)生成PEKS密文 CT ksd w （或陷门 T ksd w ），并将结果返回给 A。在挑战阶段，当收到 A发来的两个挑战关键词 w 0 , w1 后， B并不向签名预言机查询 w b 以获取签名 σ w b ，而是随机选取 r，并通过将 r视作wb 的签名来生成关于 w b 的挑战PEKS密文和陷门(CT ∗, T ∗ )。随后 A将(CT ∗, T ∗ )发送给 A。在查询II阶段， B的模拟方式与查询I阶段相同。在输出阶段，当A输出其对 b的猜测 b ′后， B从输入元素中选取一个

̂随机预言机 H随机地输出其伪造签名。设 Q为事件 A向随机预言机 H查询(wb, σwb)的事件。则 A在上述游戏中获胜的优势为AdvSS CKGA SS ‐,A= Pr [b′= b|Q]+Pr[b′= b|Q]−1/2.。可以注意到，在上述模拟中，如果事件 Q未发生，即 A从未以(wb, σwb)查询 H，那么由于随机预言机̂H的性质，从 A的角度来看，上述游戏与原始的SS‐CKGA游戏完全相同。然而，在此种情况下， A在此游戏中获胜的概率至多为 1/2，因为(CT∗, T∗)与 b相互独立，即Pr[b′= b|Q]= 1/2。因此，我们有Pr[b′= b|Q]= AdvSS CKGA SS A ‐,，这意味着事件Q发生的概率为AdvSS CKGA SS A ‐,。因此，若对̂H的查询次数为qĤ，则 B能够以优势AdvOMU BS, B ≥ 1/qĤ · AdvSS CKGA SS A ‐,成功伪造一个签名(wb, σwb)。

IND‐CKA安全性 。对于IND‐CKA安全性，它保证了除了用户之外，其他任何实体都无法获知用户的私有输入（关键词）的任何信息，我们有以下定理。

定理2 。如果存在一个多项式时间敌手 A能够以优势Adv IND CKA KS A-,攻破上述方案 SA-PEKS的IND-CKA安全性，则存在一个多项式时间敌手 B能够以至少为Adv Blindness BS ,B ≥ AdvIND CKA KS A-,的优势攻破底层签名方案 BS的盲性安全性。

证明：我们通过构建一个算法 B来证明上述定理，该算法将对手 A作为子程序运行，以攻破底层方案 BS的盲性安全性，具体如下。假设在针对方案 BS的盲性安全攻击游戏中的挑战者为 C。

在设置阶段， B从 C接收公钥/私钥对（pk, sk），将该密钥对发送给 A，然后从 A接收挑战关键词（w0, w1）。 B 随后将（w0, w1）作为挑战消息转发给 C。在挑战阶段， B 在 C的视角下模拟为对抗性签名者，在 A的视角下作为针对方案 SA‐PEKS的IND‐CKA游戏的挑战者。一旦 C开始第一次执行签名协议， B便与 A启动密钥服务器导出的关键词签发协议，并在 A和 C之间转发消息。在协议的第二次执行期间， B使用公钥/私钥对（pk, sk）与 C诚实交互。在输出阶段，当 A输出其猜测 b′后， B将 b′作为其对 C的猜测输出。

很容易看出，从 A的角度来看，上述模拟与IND‐CKA游戏是不可区分的。因此，我们有Adv Blindness BS ,B ≥ Adv IND CKA KS A ‐,,，证明完成。

OMU‐CKA安全性 。下面我们讨论我们提出的通用转换的 OMU‐CKA安全性。该概念保证了即使用户之前已看到许多 KS派生关键词，若无密钥服务器的帮助，也无法伪造出新的 KS派生关键词。形式化地，我们有以下定理。

定理3 . 如果存在一个多项式时间敌手 A能够以优势Adv O M U CKA U A -, 攻破上述方案SA-PEKS的OMU-CKA安全性，则存在一个多项式时间敌手 B，能够以至少AdvOMU BS,B ≥ Adv OMU CKA U A -,的优势攻破底层签名方案 BS的一次性不可伪造性安全性。

证明：我们通过构造一个算法 B来证明上述定理，该算法调用对手 A以攻破方案BS的一更多不可伪造性安全性，具体如下。

在设置阶段， B从签名预言机接收公钥 pkks，并向 pkks发送 A。在KSD查询阶段，当接收到被查询的关键词 w 时， B向签名预言机查询 w以获得签名 σw，并将返回签名的哈希值作为̂( H,w)返回给 σw，作为关键词 A的KS派生关键词。在输出阶段，如果 w输出了 A个有效对 qk+ 1({,wi) ksdwi，其中}1≤i≤qk+1为KS派生关键词查询次数。然后对于每个 qk， i在哈希查询记录中查找 B对应的签名 wi，并输出 σi({,wi) σi作为}1≤i≤qk+1有效消息/签名对，即其伪造签名。否则， qk+ 1中止。

可以看到，从对手 A的角度来看，上述由 B进行的模拟与原始的OMU‐CKA游戏是不可区分的，因此 A能够以优势 AdvOMU CKA U A ‐,(λ)成功输出qk+ 1个有效的关键词/KS派生关键词对。也就是说， B能够以至少Adv OMU BS,B ≥Adv OMU CKA U A ‐, 的优势攻破 BS的一次性多不可伪造性安全性。

根据上述定理，我们得到以下观察结果。

定理4 。如果底层盲签名在一次性不可伪造性和盲性方面是安全的，那么上述通用转换将产生一个安全的SA-PEKS方案。

关于多层级安全的进一步讨论。理想情况下，我们希望对手无法获得对密钥服务器KS的授权访问。这意味着对手既不能发起离线也不能发起在线关键词猜测攻击（on‐lineKGA）。然而在现实中，对手（包括对抗性存储服务器adversarialSS）可能具有对密钥服务器KS的远程访问权限。在这种情况下，只要底层PEKS是SS‐CKA安全的，所得到的SA‐PEKS仍然是SS‐CKA 安全的。但我们应注意，即使在此情形下，对抗性存储服务器也无法高效地发起关键词猜测攻击（KGA），因为它必须通过协议以在线方式对每一个猜测关键词w进行签名查询，从而使得暴力破解攻击效果大大降低。如第6.1节所示，通过有效的限速机制，可以显著减缓在线关键词猜测攻击（on‐lineKGA）的速度。

3.4 针对好奇密钥服务器的更强安全性

有人可能会担心，好奇的密钥服务器KS也能够通过截获存储服务器SS与接收者之间通信信道上传输的陷门来发起离线关键词猜测攻击。为了实现针对此类好奇密钥服务器的更强安全性，我们可以采用无安全信道的可搜索加密（S CF‐PEKS）[11],[12],[18]的思想。该方案的可行性在于我们所提出的方案可以透明地与任何现有的PEKS系统协同工作，因此上述通用转换同样适用于SCF‐PEKS。

示意图1

4 SA‐PEKS的实例化

4.1 底层方案

根据上述通用转换，这里我们展示一个基于FDH‐RSA盲签名[19]和Boneh等人在[3]中提出的PEKS方案（称为 BCOP‐PEKS）的所提议SA‐PEKS方案的实例化。我们首先介绍这两个构建模块。

FDH‐RSA 。RSA盲签名在图2中描述。签名者具有公钥 N, ̂e 和私钥 N, d，其中̂ed ≡ 1 mod φ(N)，模数 N是两个长度大致相等的不同素数的乘积。用户使用哈希函数 H: {0, 1}∗ → Z∗ N将消息 m哈希为 ZN中的一个元素，然后使用随机群元素 r←$ Z∗ N对该结果进行盲化。生成的盲化哈希值记为m，然后发送给签名者。签名者通过计算 σ←(m)d mod N，使用其私钥 d对 m进行签名，并将 σ返回给用户。用户随后通过 σ ← r−1σ mod N移除盲化因子以获得签名。正确性可由以下事实得出： σ=(m)d mod N= (r̂eH(m))d mod N=(m)d mod N，因此 σ= r−1σ mod N。

我们可以看到，上述FDH‐RSA的盲性安全性由用于对签名消息进行盲化的随机一次性元素所保证。至于不可伪造性安全性，根据[19],的结果，若RSA已知目标逆问题是困难的，则FDH‐RSA盲签名方案在面对一次多伪造攻击时具有多项式安全性。更多细节可参见[19]。

BCOP‐PEKS 。这里我们展示在[3]中提出的PEKS方案。该方案基于计算性Diffie‐Hellman问题的一种变体。设 G1、 GT为两个具有相同素数阶 p的乘法群。令 g为 G1的生成元， I为 GT的单位元。对称双线性映射是一个映射 e: G1 × G1 → GT，满足对所有 u、 v ∈ G1和 a、 b ∈ Z p 都有e(u a, v b )= e(u, v) ab。值得注意的是， e可以被高效计算，且e(g, g) 6= I。随后，该非交互式可搜索加密方案工作如下。

密钥生成算法 。输入的安全参数决定群组p的大小 G 1 ， G T 。然后该算法选择一个随机的 α $ ← Z∗ p ，一个 G 1 的生成元 g，并选择两个哈希函数 H 1 ：{0, 1} ∗→ G 1 和 H 2 ：G T →{0, 1} lo g p。然后输出 pk R =（g， h= g α， H 1 ， H 2 ） sk R = α。
PEKS 。对于关键词 w，选择一个随机数 r ←$ Z∗ p并计算 t= e (H1(w) hr)。然后发送者将PEKS密文输出为 CTw=(gr, H2(t))。
陷门。对于关键词 w′，接收者将陷门输出为 Tw′= H1(w′) α ∈ G1。
Test 。服务器以 CTw=(A, B)和 Tw′作为输入，如果 H2(e(Tw′, A))= B，则输出 T rue，否则输出 F alse。

上述PEKS方案的正确性易于获得。在安全性方面，该方案能够抵御SS‐CKA[3]，但无法抵御离线KGA。实际上，针对BCOP‐PEKS方案的离线KGA可以以更简单的方式发起。给定一个陷门Tw∗= H1(w ∗)α，攻击者可以通过验证 e(Tw∗, g) =? e(H1(w) h)，轻松测试其猜测关键词 w是否为Tw∗的底层关键词。

4.2 生成的 SA‐PEKS

这里展示了由FDH‐RSA和BCOP‐PEKS方案导出的 SA‐PEKS。详细内容如图3所示。请注意，我们的方案中的基于KS的关键词生成协议要求用户
示意图2

要求用户验证 N< ̂e。这是为了避免密钥服务器可能通过不诚实地生成密钥来获取有关关键词的某些信息。该条件确保了即使 N被恶意生成，gcd(φ(N) ̂e) = 1仍成立，从而保证映射 f̂e: Z∗ N→ Z∗ N（定义为对所有 x ∈ Z∗ N满足 f̂e(x)= x̂e mod N）是 Z∗ N上的一个置换。由于 f̂e是一个置换，并且用户可以验证签名的有效性，因此即使存在恶意密钥服务器，也无法强制签名输出为某一固定值。很容易看出，对于任意两个关键词 w, w′，如果w= w′，则 ksdw= Ĥ( = Ĥ σw w w′ H w′ d= ksdw′ , )= Ĥ(, H()d)(,())。因此，对于相应的 PEKS密文 CTksd w =(A, B) 和陷门 Tksd w ′ ，我们有 H2(e(Tksd w ′ , A))= H2(e(H1(ksdw′) hr))=B。否则， H2(e(Tksd w ′ , A)) 6= Bas ksdw 6= ksdw′。安全性分析。所得到的SA‐PEKS方案的安全性可以很容易地基于定理4得出，因为FDH‐RSA是一更多次不可伪造且具有盲性。形式化地，我们有以下合谋。推论1.上述具体的SA-PEKS方案是安全的。

5 实现与性能

5.1 客户端‐KS协议

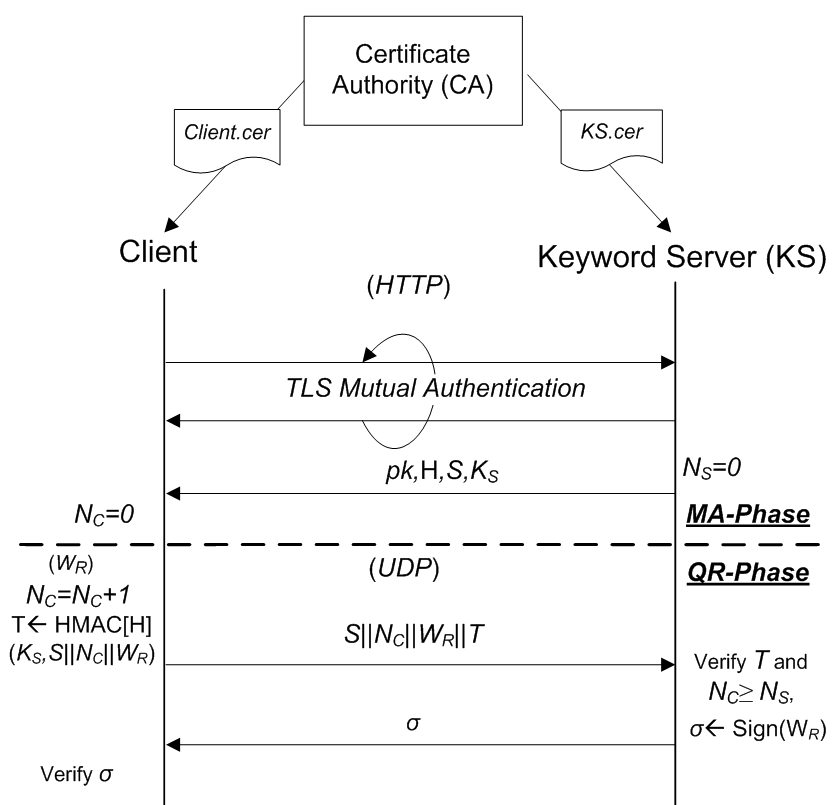
受[20],工作的启发，我们提出了一种用于客户端与密钥服务器（KS）交互的协议及限速策略，以限制客户端查询，减缓在线关键词猜测攻击。我们的设计目标是提供一种低延迟协议，避免性能下降。该协议依赖于证书颁发机构（CA），为密钥服务器和每个客户端提供唯一的可验证TLS证书。如图4所示，协议的执行包括通过HTTP进行的相互认证（ MA）阶段和通过UDP进行的查询‐响应（QR）阶段。

示意图3

第一阶段：相互认证 。该相互认证过程以客户端发起的带相互认证的TLS握手开始。密钥服务器立即响应，提供底层盲签名方案的验证密钥 pk和一个哈希函数 H（默认为SHA‐256），一个随机会话标识符 S ∈{0, 1} 128，以及一个随机会话密钥 K S ∈{0, 1} k。密钥服务器KS随后使用此会话初始化并记录序列号为 N S = 0。客户端存储 pk, S, K S ，并同样初始化一个序列号 N C = 0。

第二阶段：查询‐响应 。在QR阶段，客户端首先生成关键词 w的盲化值 W R ，增加记录的序列号 N C ← N C + 1，然后使用密钥服务器KS的会话密钥 KS计算MAC标签，作为T ← HMAC H 。然后客户端将S||NC||WR||T通过 UDP数据包发送给密钥服务器KS。密钥服务器KS在接收到查询信息后，首先检查 NC ≥ NS并验证MAC T的正确性。如果验证失败，则密钥服务器KS将丢弃该数据包且不作任何响应；否则，它会对盲化后的关键词进行签名，并将签名 σ返回给客户端。

抵御在线KGA的每客户端速率限制机制 。我们探讨了所谓的指数延迟机制，以实现对抗在线KGA与密钥服务器请求延迟之间的平衡。对于第一个查询，密钥服务器以初始的小延迟 tI进行响应，并且来自同一客户端的每次后续查询的延迟时间将加倍。该加倍过程在达到上限 tU时停止。密钥服务器维护同步的时段和活跃客户端列表。它在每个时段结束后检查活跃客户端的状态。如果某客户端在整个时段内没有发出任何查询，则其延迟将重置为初始值。同时，对于已在活跃客户端列表中并等待响应的客户端，密钥服务器将拒绝其任何新的查询。我们指出，该策略不会给通常以较低频率发起查询的普通用户带来明显的通信延迟。

协议安全性 。攻击者可能会尝试窃听甚至篡改客户端与密钥服务器之间的通信。在该协议中，由于会话初始化阶段采用了相互认证的TLS握手，因此任何对手都无法可以启动一个会话，假装成一个有效的客户端。此外，如果没有会话密钥 KS，任何对手都无法在不成功进行MAC伪造的情况下创建一个新的查询数据包。由于随机选择的会话标识符，数据包无法在不同会话之间重放；又由于递增的序列号，数据包也无法在同一会话内重放。

协议延迟 。对于客户端‐KS协议，我们以标准方式使用 SHA256实现FDH‐RSA（RSA1024）。类似于[20],PKI配置使用RSA2048证书，并且在我们的协议中握手固定使用 ECDHE‐RSA‐AES128‐SHA密码套件。在我们的实现中，客户端设备位于大学局域网内，配备Linux系统（更准确地说， 2.6.35‐22‐generic版本），处理器为Intel(R)Core(TM)2 DuoCPU，主频3.33GHz，内存2.00GB。表1以500次试验的中位时间加减一个标准差的形式展示了不同阶段的延迟。

操作	延迟（毫秒）
Ping（1次往返时间）	96 ±02
MA阶段	312 ± 48
QR阶段（1000查询/秒）	103 ± 32
QR阶段（2000查询/秒）	134 ±43
QR阶段（3000查询/秒）	157 ±40
QR阶段（4000查询/秒）	193 ±46
QR阶段（5000查询/秒）	252 ±51
QR阶段（6000查询/秒）	327 ±49

我们可以注意到，当KS负载较低时（例如，1000次查询/秒），延迟非常小，实际上几乎是最小可能的时间（Ping操作的1 次往返时间（RTT））。随着查询速率的增长，时间也随之增加。具体而言，当查询速率为3000查询/秒时，延迟约为 157±40毫秒；当查询速率增加到7000查询/秒时，延迟变为 376±44毫秒。值得注意的是，我们在实验中仅考虑成功操作。也就是说，所有超时三次的回复均被排除在中位数计算之外。

对在线KGA的防御性能 。为了评估我们的限速机制在实际环境中的效果，我们在实验中估算了在线关键词猜测攻击对本协议的影响。在我们的协议中，所提出的限速机制（即指数延迟机制）在在线KGA速度与密钥服务器请求延迟之间实现了平衡，因为延迟会随着来自客户端的查询次数呈指数级增长。在本实验的指数延迟机制中，我们将初始小延迟 tI设为 10毫秒，将周期时长 tE设为一周。然后我们通过设置上限 t U为不同值来评估协议的性能，即最大查询速率（以每秒查询次数计）。为了评估所引入机制的有效性，我们还运行了无限制速率的协议版本。表2给出了攻击者在攻陷一个客户端后所能达到的最大查询速率。从结果可以看出，我们的指数延迟机制能够显著减缓在线关键词猜测攻击。具体而言，若不对密钥服务器进行任何限速，攻击速率约为2700次查询/ 秒。而通过强制实施指数延迟机制，攻击速率可显著降低至小于10次查询/秒。攻击速率随着上限 tU的增长而下降，当我们将 tU设为1000毫秒时，攻击速率仅为1.21次查询/秒。

设置	攻击速率(查询/秒)
无速率限制	2700
tU= 400ms	8.23
tU= 600ms	4.21
tU= 800毫秒	2.54
tU= 1000毫秒	1.21

5.2 实例化方案

5.2.1 方案比较

计算。如表3所示，与BCOP方案[3]（我们SA‐PEKS构造的底层PEKS方案）相比，我们的方案在生成PEKS密文和陷门时需要额外进行4次RSA模幂运算。在测试阶段，我们的方案的计算开销与BCOP方案相同。虽然方案[5]也能实现一定程度的抗离线关键词猜测攻击安全性，但由于额外的配对运算，其计算开销要高得多。具体而言，在我们的方案中， PEKS生成、陷门生成和测试的计算开销分别为2ExpG1 +4 ExpZ∗ N +2HashG1+ 1PairingG1,GT、11HashG1+1ExpG1 +4 ExpZ∗ N和HashG1+ 1PairingG1,GT，其中ExpG1, Exp Z∗ N分别表示在 G1 和 Z∗ N中的一次模幂运算，HashG1表示在 G1 中一次哈希操作的开销。

通信。我们比较了我们的方案与[3]和[5]中方案的通信开销，具体从PEKS密文、陷门以及返回给接收者的匹配数据集（在表3中记为Ω）三个方面进行比较。更准确地说，与底层PEKS方案[3],相比，我们的方案在每次生成PEKS密文或陷门时，需要在KS与用户之间额外传输两个 Z∗ N元素。我们指出，该结果独立于底层PEKS方案，因为我们的解决方案可透明地与任何现有PEKS系统协同工作。注意，在上述客户端‐KS协议的实现中，我们使用了FDH‐RSA（ RSA1024），因此每个用户的相应通信开销为2048比特。 [5]中提出的方案要求每个关键词对应两个PEKS密文，因此其PEKS密文大小相较于BCOP方案[3]增加了一倍。此外，从 SS传输给接收者的数据集大小对于我们的方案和BCOP方案而言相同（即Ω），而对于方案[5]则为2Ω或3Ω。

存储。关于存储成本，我们的方案仅为每个用户引入了非常小的开销。也就是说，每个用户需要在计算每个PEKS密文和陷门之前存储FDH‐RSA盲签名的公钥参数（即 N, ̂e, H）以获得KS派生关键词。值得注意的是，方案[5]要求接收者为每次查询保留精确陷门，以便从SS的数据集中过滤出不匹配的数据。

方案	PEKS密文	陷门	测试	PEKS密文	陷门	测试
	计算	计算	计算	通信	通信	通信
BCOP[3]	2ExpG1+2HashG1 + 1配对G1,GT	1HashG1 +1ExpG1	1HashG1+ 1配对G1,GT	G1+ logp	G1	Ω
XJWW[5]	4ExpG1+4HashG1 +2配对G1,GT	2 HashG1 +2指数G1	2次哈希G1+ 2次配对G1,GT	2G1+2对数 p	G1	2Ω或 3Ω
我们的方案	2ExpG1+2Exp ZN∗ +2哈希G1+ 1配对G1,GT	1HashG1+1ExpG1 +2ExpZN∗	1HashG1+ 1配对G1,GT	2Z∗ N+ G1+ logp	2Z∗ N+ G1	Ω

示意图4

示意图5

示意图6

5.2.2 实验结果

为了在实验中评估我们方案的效率，我们使用GNU多精度算术（GMP）库和基于配对的密码学（PBC）库实现了该方案。以下实验基于C语言，在配备3.33GHzIntel(R) Core(TM)2Duo处理器和2.00GB内存的Linux系统（更准确地说，版本为2.6.35‐22‐generic）上进行。对于椭圆曲线，我们选择了一条基域大小为159位的MNT曲线，|p|=160和 |q|=80。

我们主要分析了[3],[5]和我们的方案中PEKS生成、陷门生成和测试的计算开销。如图5和图6所示，在PEKS生成和陷门生成方面，我们方案的计算开销仅略高于BCOP方案。这是由于底层FDH‐RSA方案所涉及的计算量非常小。由于我们的方案在测试阶段未引入任何额外操作，因此相应的计算开销与底层PEKS系统保持一致，如图7所示。

至于[5]中的方案，虽然其在抵御离线KGA方面达到了一定的安全性，但在所有操作上的计算开销均高于[3]中的 PEKS方案以及我们的方案。特别是当关键词数量为50时， [5]中方案生成一个PEKS密文大约需要2秒，而该方案的在[3]中，我们的方案分别约为0.9秒和1秒。对于陷门生成，由于 G1中的指数运算通常比Z∗ N中的指数运算更耗时，因此其计算开销略高于我们的方案。具体而言，在[5]中生成 50个关键词的陷门时间约为0.12秒，而我们的方案为0.08秒。关于测试操作，[5]中的计算开销几乎是我们的方案的两倍。具体来说，[5]方案的测试计算开销约为1.6秒，而我们的方案为0.8秒。这是因为[5]中的测试需要额外的一次配对运算。

6 结论

在本研究中，我们通过形式化一种新的PEKS系统——服务器辅助的基于关键词搜索的公钥加密（SA‐PEKS），对（内部）离线关键词猜测攻击提供了一种实用且可行的解决方案。我们提出了一种从任意PEKS方案到安全的SA‐PEKS方案的通用转换方法，并给出了SA‐PEKS方案的首个实例化，同时展示了如何通过限速机制安全地实现客户端‐KS协议以抵御在线关键词猜测攻击。实验结果表明，我们提出的方案在提供对离线和在线KGA抵抗能力的同时，具有更高的效率。