VP牛客小白月赛88（A---F)（收获很多）

最新推荐文章于 2025-11-25 00:06:26 发布

原创最新推荐文章于 2025-11-25 00:06:26 发布 · 574 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

博客分享了算法题的解题思路与代码。提到题目难度梯度大，用map+并查集思想化解难题，给出递推式优化复杂度；还涉及光反射路径模拟、01DP、纯模拟等题的解题方法，以及贪心水题，同时给出相关AC代码和注意事项。

感觉难度梯度有点大，前4个都十分基础，E和F比较的难，直接看题（按照个人的收获从大到小排）

可以用启发式合并但是太菜了还不会（等以后来填坑），这里用map+并查集的思想来十分巧妙地化解。

我们令next[L][i]表示只有后L个操作序列，i变成了next[l][i]，我们假设倒数第l+1个操作为把3变成6，容易得到递推式：

next[l][4]=next[l+1][4]....next[l+1][3]=next[l][6].这样我们可以得到从l--->l+1,除了该次命令外的值都相同，只改变了该次命令涉及的，这样子我们就可以舍弃第一维，这样子从反向建边时间与空间复杂度都可以了。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int t,n,m,x[1000100],y[1000100],a[1000100];
map<int,int> fa;
void solve(){
    for(int i=m;i>=1;i--){
       if(fa.count(y[i])){
           fa[x[i]]=fa[y[i]];
       }
        else fa[x[i]]=y[i];
    }
    for(int i=1;i<=n;i++){
        if(fa.count(a[i])==0) cout<<a[i]<<" ";
        else cout<<fa[a[i]]<<" ";
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>t;
    while(t--){
        fa.clear();
        cin>>n>>m;
        for(int i=1;i<=n;i++) cin>>a[i];
        for(int i=1;i<=m;i++) cin>>x[i]>>y[i];
        solve();
        cout<<endl;
    }
}

我们直接看最左上的方块沿着ur方向模拟光的反射路径图，下面是实现该模拟代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,d,ansx,ansy,ans;
bool vis[2100][2100];
struct node{
    int x,y;
};
queue<node> q;
int dx=-1,dy=1;
int main(){
    cin>>n>>m;
    vis[1][1]=1;
    q.push({1,1});
    while(!q.empty()){
        node ck=q.front();
        q.pop();
        int xx=ck.x+dx,yy=ck.y+dy;
        if((xx==0&&yy==0)||(xx==n+1&&yy==m+1)||(xx==0&&yy==m+1)||(xx==n+1&&yy==0)){
            break;
        } 
        if(xx==0){
            dx=-dx;
            if(vis[1][yy]) break;
            vis[1][yy]=1;
            q.push({1,yy});
        }
        else if(yy==0){
           dy=-dy;
            if(vis[xx][1]) break;
            vis[xx][1]=1;
            q.push({xx,1}); 
        }
        else if(xx==n+1){
            dx=-dx;
            if(vis[n][yy]) break;
            vis[n][yy]=1;
            q.push({n,yy});
        }
        else if(yy==m+1){
           dy=-dy;
            if(vis[xx][m]) break;
            vis[xx][m]=1;
            q.push({xx,m}); 
        }
        else{
            if(vis[xx][yy]) break;
            vis[xx][yy]=1;
            q.push({xx,yy});
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cout<<vis[i][j];
        }
        cout<<endl;
    }

}

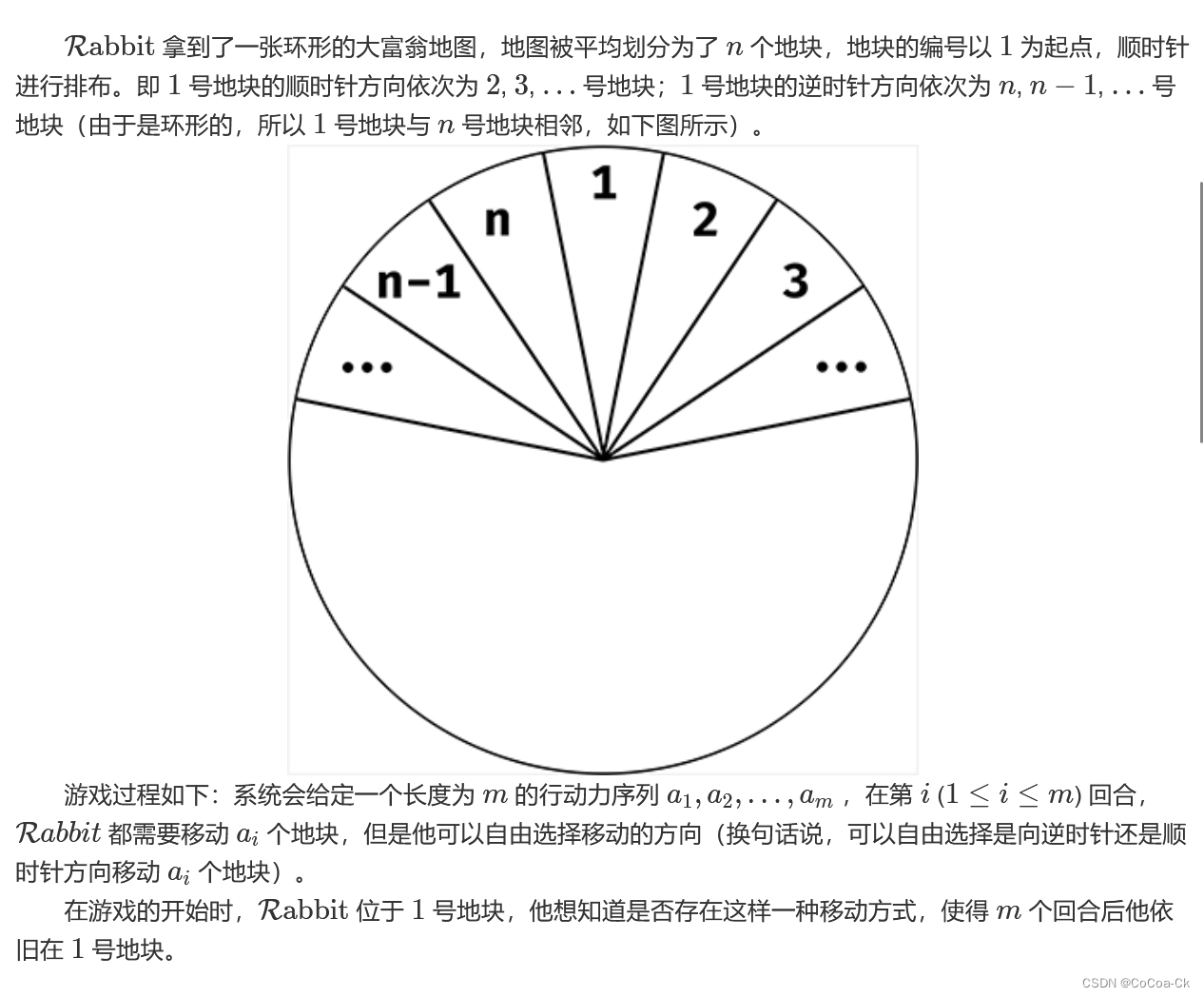
简单的01DP，加一个处理循环条件的即可。下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,a[6000];
bool dp[5100][5100];
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++) scanf("%d",&a[i]);
    for(int i=1;i<=m;i++) a[i]=a[i]%n;
    dp[0][1]=1;
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            int k1=(j-a[i]+n-1)%n+1;
            int k2=(j+a[i]-1)%n+1;
            dp[i][j]=dp[i-1][k1]||dp[i-1][k2];
        }
    }
    if(dp[m][1]==1) cout<<"Yes";
    else cout<<"No";
}

纯模拟，直接上代码：

#include<bits/stdc++.h>
using namespace std;
int n,h,m;
int a[2000];
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>h>>m;
        int ck=60*h+m;
        a[ck-1]=1;
        a[ck-3]=1;
        a[ck-5]=1;
    }
    int cnt=0;
    for(int i=1;i<=2000;i++){
        if(a[i]) cnt++;
    }
    cout<<cnt<<endl;
    for(int i=1;i<=2000;i++){
        if(a[i]){
            cout<<i/60<<" "<<i%60<<endl;
        }
    }
}

两点注意：

1.用&之类的记得整体加个括号。

2.含有空格的字符串可以用getline(cin, )来实现：

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
char op,c;
string a[6];
int main(){
    for(int i=1;i<=5;i++){
        getline(cin,a[i]);//有空格的字符串
    }
    if(a[3][5]=='&'){
        cout<<((a[2][0]-'0')&(a[4][0]-'0'));//加括号！！！
    }
    else if(a[3][5]=='='){
        cout<<((a[2][0]-'0')|(a[4][0]-'0'));
    }
    else cout<<(1-(a[3][0]-'0'));
}

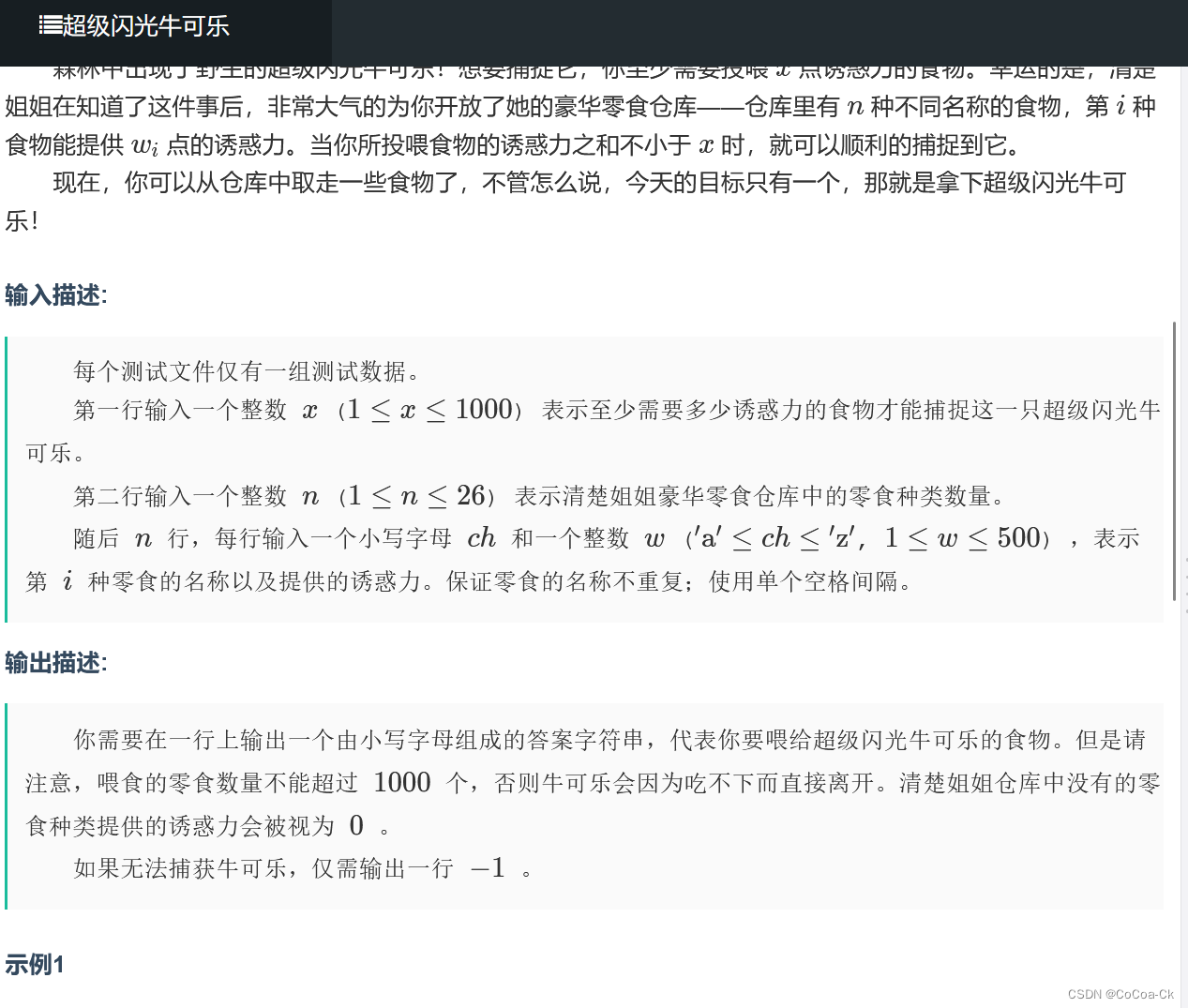
一道贪心水题：

#include<bits/stdc++.h>
using namespace std;
int x,n,max1,w;
char a,b;
int main(){
    cin>>x;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a>>w;
        if(w>max1){
            max1=w;
            b=a;
        }
    }
    int ck;
    if(x%max1==0) ck=x/max1;
    else ck=x/max1+1;
    if(ck>1000) cout<<-1;
    else{
        for(int i=1;i<=ck;i++) cout<<b;
    }
}