备战蓝桥杯---线段树基础2

最新推荐文章于 2025-11-25 00:02:19 发布

原创最新推荐文章于 2025-11-25 00:02:19 发布 · 721 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #算法 #c++ #线段树

本文介绍了如何在处理线段树中涉及乘法操作时使用懒标记来解决括号问题，详细解释了标记下移规则以及在AC代码中的应用实例，展示了区间修改和计算的方法。

今天我们把线段树的另一个模板看一下：

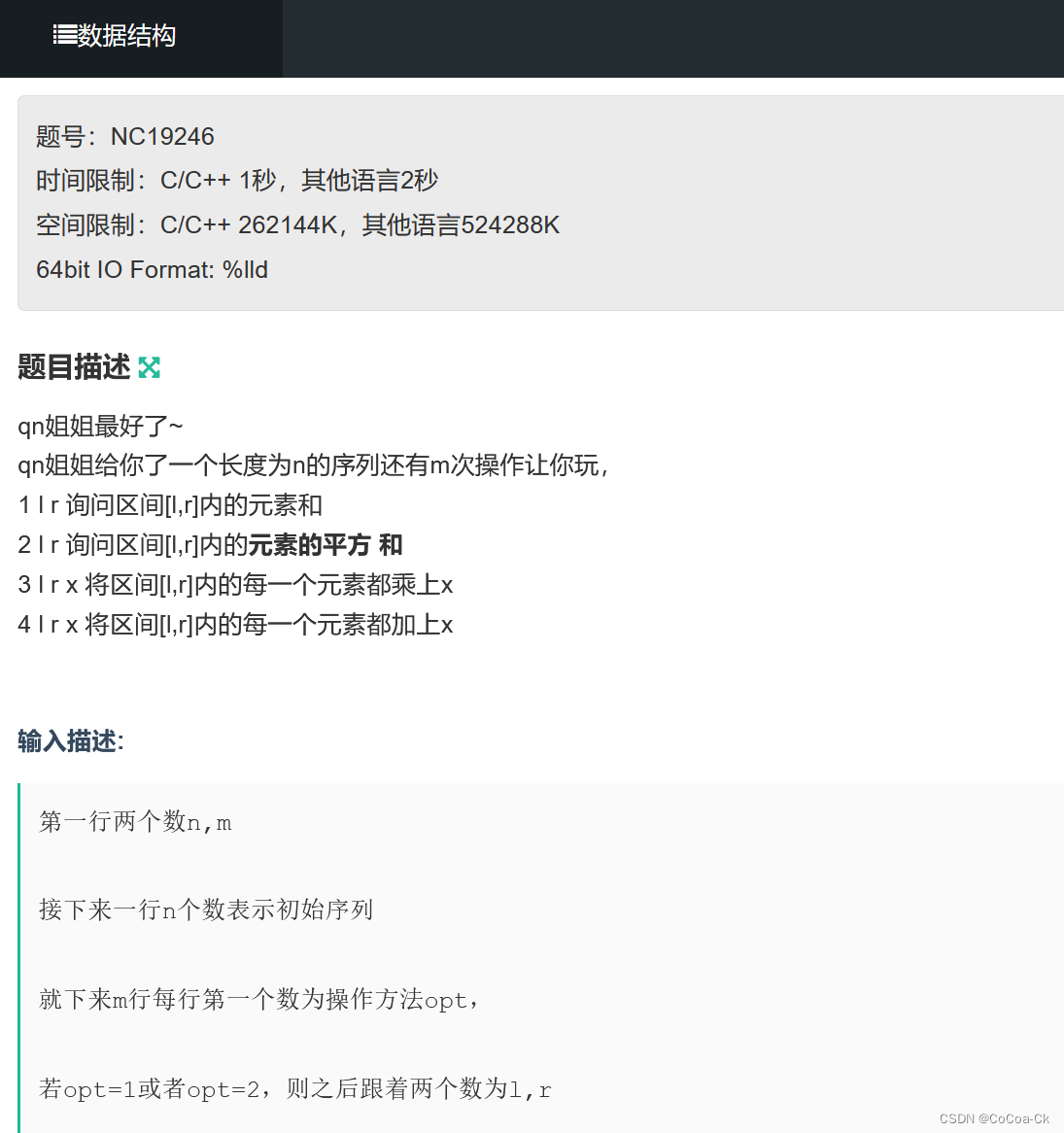
在这里，我们注意到乘的操作，因此我们用两个懒标记来分别表示加和乘，这时我们面临了一个问题，就是当我们把标记往下传时，它的儿子怎么知道是先乘还是先加？

究其原因，其实是括号在作祟，因此，我们每一次乘的时候，出了lazy*=num,我们把加法的标记也乘一下，这样子我们先乘后加，就巧妙地化解了括号的问题。

同时，还有一点我们需要注意，那就是当标记下移时，子节点的加法标记出了加上父节点的加法标记，还要*父节点的乘法标记。

举个例子，考虑原来的儿子为*2+3,父亲的懒标记也是*2+3,当我们下放时，应该变成*4+9，而其中的9就是由3+3*2得到的。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a[10001],m,sum[4*10001];
int tree[4*10001];
int lazy1[4*10001];
int lazy2[4*10001];
void pushdown(int p,int l,int r);
int calc(int p,int l,int r,int x,int y,int k);
void build(int p,int l,int r){//建树 
    lazy2[p]=1;
	if(l==r){
		tree[p]=a[l]*a[l];
		sum[p]=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	tree[p]=tree[p*2+1]+tree[p*2];
	sum[p]=sum[p*2+1]+sum[p*2];
	return;
}
void pushdown(int p,int l,int r){//lazy标记下移 
	int mid=(l+r)/2;
	lazy1[p*2]=(lazy2[p])*lazy1[p*2]+lazy1[p];
	lazy1[p*2+1]=lazy1[p*2+1]*(lazy2[p])+lazy1[p];
    lazy2[p*2]*=lazy2[p];
	lazy2[p*2+1]*=lazy2[p];
	tree[p*2]=(lazy2[p])*(lazy2[p])*tree[p*2]+2*lazy1[p]*(lazy2[p])*sum[2*p]+lazy1[p]*lazy1[p]*(mid-l+1);//更新子节点的值 
	tree[p*2+1]=(lazy2[p])*(lazy2[p])*tree[p*2+1]+2*lazy1[p]*(lazy2[p])*sum[2*p+1]+lazy1[p]*lazy1[p]*(r-mid);
    sum[p*2]*=(lazy2[p]);
	sum[p*2+1]*=(lazy2[p]);
	sum[p*2]+=lazy1[p]*(mid-l+1);
	sum[p*2+1]+=lazy1[p]*(r-mid);
	lazy1[p]=0;//自己因为下移清0 
    lazy2[p]=1;
}
void change1(int p,int l,int r,int x,int y,int num){
	if(x<=l&&r<=y){
		tree[p]+=2*num*(sum[p])+num*num*(r-l+1);
		sum[p]+=num*(r-l+1);
		lazy1[p]+=num;
		return;
	}
	if(lazy1[p]!=0||lazy2[p]!=1){//区间部分修改，需要下移 
		pushdown(p,l,r);
	}
	int mid=(l+r)/2;
	if(y<=mid) change1(p*2,l,mid,x,y,num);
	if(x>mid) change1(p*2+1,mid+1,r,x,y,num);
	if(x<=mid&&y>mid){
	change1(p*2,l,mid,x,mid,num);
	change1(p*2+1,mid+1,r,mid+1,y,num);}
	tree[p]=tree[2*p]+tree[2*p+1];
	sum[p]=sum[2*p]+sum[2*p+1];
	return;
}
void change2(int p,int l,int r,int x,int y,int num){
	if(x<=l&&r<=y){
        tree[p]=num*num*tree[p];
		sum[p]*=num;
		lazy2[p]*=num;
        lazy1[p]*=num;
		return;
	}
	if(lazy1[p]!=0||lazy2[p]!=1){//区间部分修改，需要下移 
		pushdown(p,l,r);
	}
	int mid=(l+r)/2;
	if(y<=mid) change2(p*2,l,mid,x,y,num);
	if(x>mid) change2(p*2+1,mid+1,r,x,y,num);
	if(x<=mid&&y>mid){
	change2(p*2,l,mid,x,mid,num);
	change2(p*2+1,mid+1,r,mid+1,y,num);}
	tree[p]=tree[2*p]+tree[2*p+1];
	sum[p]=sum[2*p]+sum[2*p+1];
	return;
}
int calc(int p,int l,int r,int x,int y,int k){
	if(l>=x&&r<=y){
		if(k==1) return tree[p];
		else return sum[p];
	}
	if(lazy1[p]!=0||lazy2[p]!=1){
		pushdown(p,l,r);
	}
	int mid=(l+r)/2;
	if(y<=mid) return calc(p*2,l,mid,x,y,k);
	if(x>mid) return calc(p*2+1,mid+1,r,x,y,k);
    return calc(p*2,l,mid,x,mid,k)+calc(p*2+1,mid+1,r,mid+1,y,k);
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
	build(1,1,n);
	for(int i=1;i<=m;i++){
		int x,y,k,op;
		scanf("%lld%lld%lld",&op,&x,&y);
		if(op==1){
            printf("%lld\n",calc(1,1,n,x,y,0));
		}
		else if(op==2) printf("%lld\n",calc(1,1,n,x,y,1));
        else if(op==3){
            scanf("%lld",&k);
            change2(1,1,n,x,y,k);
        }
        else{
            scanf("%lld",&k);
            change1(1,1,n,x,y,k);
        }
	} 
}