深度学习第二阶段之线性代数①

涉及到的高数部分

1. 理解梯度的概念和意义

2. 两个符号
   $$\Sigma f(x)和\int f(x)dx$$
   可以等价得理解为求积分符号

3. 了解函式的定义域，值域，饱和性，单调性，周期性，对称性

4. 两个基本函数

   ① log函数：压缩，方便计算
   ② sigmoid函数：压缩到[0,1],用于求概率
   

   关于sigmoid函数的思考：
   sigmoid函数本身是饱和函数，即在0和附近梯度较大，而远离0的位置，梯度很小，所以梯度下降时要特别主要控制取值范围。所以一般不用做激活函数，而作为输出函数，求概率；
   同样tanH也会是饱和函数（虽然比sigmoid表现好一点），所以一般会用RELU函数作为激活函数约束

理解线性

线性方程组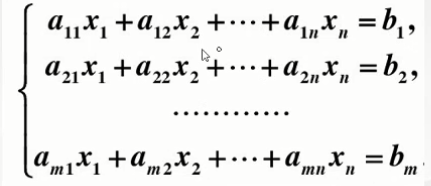
　由线性方程组未知量的系数构成的矩阵
　

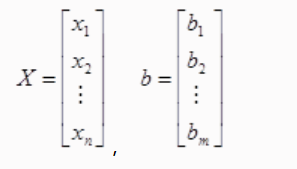
理解过拟合

过拟合可以理解为参数量过多，而数据过少。
过拟合 正常 欠拟合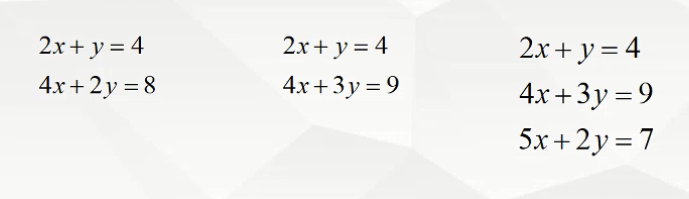

理解线性可分和线性不可分

在二维平面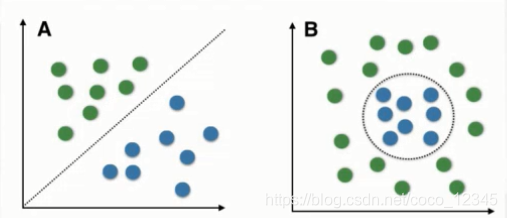
解决线性不可分的问题：用核方法升维，升到高维空间

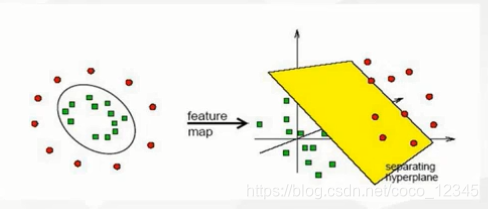
张量

0维，1维，2维，3维及以上

范数

例子

【1，2】的L2范数（模） ：
$$\sqrt{1^2+2^2}$$
L1范数就是绝对值相加

归一化

将数据限制在【-1，1】之间的操作叫做归一化

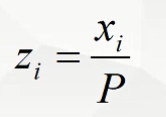
二范数归一化：P=Xi的L2范数

行列式

矩阵必须是方阵

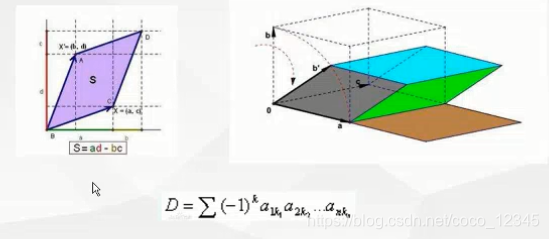
行列式 = 0 的矩阵称为奇异矩阵，反之称为非奇异矩阵