深度学习第二阶段之线性代数②

矩阵和张量的基本运算

矩阵的运算

1. 加减：形状相同，对应位置相加相减（矩阵必须同形）
2. 数加/数减：矩阵的每个位置跟一个数相加，相减
3. 点乘：要求两个矩阵必须同样形状大小，矩阵各个对应元素相乘
4. 数乘：矩阵的每个位置跟一个数相乘
5. 叉乘：前一个矩阵的列需要和后一个矩阵的行一致，不满足乘法交换律（AB≠BA）

import torch
a = torch.tensor([[1,2],[3,4],[5,6]])
b = torch.tensor([[5,6],[7,8]])
print(a*a) #点乘
print(a@b) #叉乘

张量的运算

前几项和矩阵相同
张量的叉乘： [N,X,Y] @[N,Y,C] = [N,X,C] 注意看形状

转置

矩阵的转置

import torch
a = torch.tensor([[1,2],[3,4],[5,6]],dtype=torch.float32)
print(a)
print(a.T)

tensor([[1., 2.],
        [3., 4.],
        [5., 6.]])
tensor([[1., 3., 5.],
        [2., 4., 6.]])

张量的转置
N H W C 转成 N C H W

c = torch.randn((1,5,6,3))
print(c.shape)
c_trans = c.permute(0,3,1,2)
print(c_trans.shape)

torch.Size([1, 5, 6, 3])
torch.Size([1, 3, 5, 6])

逆和违逆

1. 逆的运算相当于矩阵的除法运算
2. 只有非奇异方阵才有逆
3. 违逆是逆的推广，去除了方阵的限制

当x是方阵时：
y = w*x
w = y/x = y * $x^{-1}$ 此时$x^{-1}$ 就是x的逆
当x不是方阵时：
y = wx
w = y/x = y * $x^T$ / x * $x^T$ (此时x * $x^T$就是方阵了)
= $({x\ast x^T)}^{-1}$ *$x^T$ y（最小二乘法）

$({x\ast x^T)}^{-1}$ *$x^T$就是x的违逆

最小二乘法公式

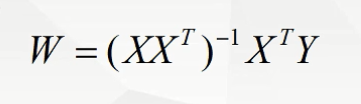
import numpy as np
x = np.array([[1],[3],[6]])
y = x*4

inv_x = np.linalg.inv((x.T).dot(x))
print(inv_x)
print(inv_x @ x.T @y)

[[0.02173913]]
[[4.]]

其他特殊矩阵

方阵
斜对角阵（主对角线之外的元素皆为0的矩阵）
单位矩阵 （对角线上是1，其他都为零）
对称矩阵（与对角线对称）
零矩阵
稀疏矩阵（大部分是0，少部分有之值）