Logistic回归
2017年03月27日 22:02
1. logistic回归的基本思想
logistic回归是一种分类方法,用于两分类问题。目的是构建一条直线y=a+x1*a1+x2*a2+.....。将x带入进这个函数中得出的值再带入到sigmoid中从而映射出之,使得大于0.5的为1类小于0.5的为2类。
其基本思想为:
a. 寻找合适的假设函数,即分类函数,用以预测输入数据的判断结果;
b. 构造代价函数,即损失函数,用以表示预测的输出结果与训练数据的实际类别之间的偏差;
c. 最小化代价函数,从而获取最优的模型参数。
2. 逻辑回归的过程
逻辑函数(sigmoid函数):
该函数的图像:
假设函数(分类函数):
判定边界:
线性边界和非线性边界如下:
图1 线性边界 图2 非线性边界
线性边界的边界形式:
非线性边界的边界形式可表示为:
hθ(x)函数的值表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
(概率公式)
代价函数为:
其中:
,
等价于:
代入得到代价函数:
这样构建的 Cost(hθ(x),y)函数的特点是:当实际的 y=1 且 hθ 也为 1 时误差为 0,当 y=1 但 hθ 不为 1 时误差随着 hθ 的变小而变大;当实际的 y=0 且 hθ 也为 0 时代价为 0,当 y=0且hθ 不为 0 时误差随着 hθ 的变大而变大。简单说为什么将y的值用作概率,这是因为对于sigmoid函数来说y越大就意味着y=1的概率越大(当然这是对于x>0的情况来说的,而对于x<0的时候就是用1-h(x)来表示其接近0的概率,而不能直接用y表示,y只能表示值而不能表示它接近0的概率),我们这个函数就是为了让所有点的概率和最大,也就是让各自的y等于1或者等于0的概率最大,这样才能对节点进行最优分类,和对新节点进行的最优识别。
实际上,Cost函数和J(θ)函数是基于最大似然估计推导得到的。
前面的概率公式可简化为:
对应的似然函数为:
对数似然函数为:
最大似然估计就是要求得使l(θ)取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。
前面提到的代价函数即可表示为:
使用梯度下降法求J(θ)的最小值(当然也可以用梯度上升法求最大值,就是把-变成+),θ的更新过程:
其中:α学习步长。
求偏导:
更新过程可改写为:
α为一常量,所以1/m一般将省略,所以最终的θ更新过程为:
求解过程中用到如下的公式:
梯度下降算法的向量化解法(如果对于矩阵的计算不好理解的话,就先看随机梯度上升法,它是用数组进行计算更符合实际的理解):
训练数据的矩阵形式表示如下,其中x的每一行为一条训练样本。
参数θ的矩阵形式为:
计算x.θ(点乘)并记为A:
求hθ(x)-y并记为E:
g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。由上式可知hθ(x)-y可以由g(A)-y一次计算求得。
θ更新过程,当j=0时:
θj同理:
综合起来:
综上所述,vectorization后θ更新的步骤如下:
(1)求A=x.θ;
(2)求E=g(A)-y;
(3)求θ:=θ-α.x'.E,x'表示矩阵x的转置。
也可以综合起来写成:
正则化逻辑回归:
假设函数:
梯度下降法最小化该代价函数:
注:计算的时候要把输入的参数中加一列x0,都是1,这样是为了回归函数中,y=x1xa1+x2+a2+b。中的b
话不多说直接上代码
#coding=utf-8
import numpy
import matplotlib.pyplot as plt
def getDataSet():
#参数只有x1和x2,但是每个参数都添加一个1,为了得出ax+b中的常数b
dataMat=[
[1.0,1.0,1.0],
[1.0,2.0,2.0],
[1.0, 3.0, 2.0],
[1.0, 1.0, 5.0],
[1.0, 4.0, 5.0],
]
labelMat=[1,0,0,1,0]
return dataMat,labelMat
def sigmoid(inx):
return 1.0/(1+numpy.exp(-inx));
def getParm(dataMat,labelMat):
dataMat=numpy.mat(dataMat)
labelMat=numpy.mat(labelMat).transpose()
#获取行列数
m,n=numpy.shape(dataMat);
#步长
a=0.1
#参数为n行1列
parm = numpy.ones((n,1));
#根据梯度上升导出的上述公式取得最优参数
#矩阵乘法是将左边的行以此和右边的列依次相乘求和,组成一个左边的行和右边的列的矩阵
for i in range(500):
y = sigmoid(dataMat * parm)
error = labelMat - y
parm = parm + a*dataMat.transpose() * error
return parm
#随机梯度上升法
def getRandomParm(dataMat,labelMat,itemNum=150):
dataMat=numpy.array(dataMat)
labelMat = numpy.array(labelMat)
m,n=numpy.shape(dataMat)
parm=numpy.ones(n)
for j in range(itemNum):
dataIndex=list(range(m))
for i in range(m):
#每次从数组中随机取出一项,用这一项更新系数,这样可以减少周期性的波动。
a = 4 / (1.0 + j + i) + 0.1
index=int(numpy.random.uniform(0,len(dataIndex)))
error = labelMat[index] - sigmoid(sum(dataMat[index] * parm))
parm += a*error * dataMat[index]
del(dataIndex[index])
return parm
def printFit(parm):
dataMat, labelMat = getDataSet()
dataMat=numpy.array(dataMat)
n=numpy.shape(dataMat)[0]
x1=[]
y1=[]
x2=[]
y2=[]
for i in range(n):
if int(labelMat[i])==1:
x1.append(dataMat[i,1])
y1.append(dataMat[i, 2])
else:
x2.append(dataMat[i, 1])
y2.append(dataMat[i, 2])
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
ax.scatter(x1,y1,s=30,c='red',marker='s')
ax.scatter(x2,y2,s=30,c='blue')
x=numpy.arange(-6.0,6.0,0.1)
y=(-parm[0]-parm[1]*x)/parm[2]
ax.plot(x,y.T)
plt.xlabel('X1')
plt.xlabel('X2')
plt.show()
dataMat,labelMat=getDataSet()
parm=getParm(dataMat,labelMat)
print(parm)
print(sigmoid(dataMat*parm))
printFit(parm)
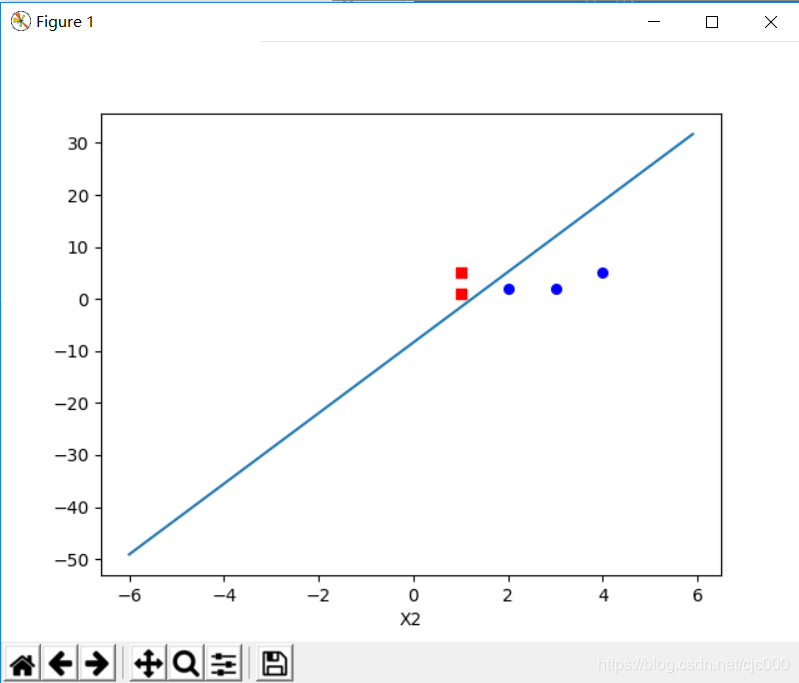
参考:








 本文详细解析了Logistic回归的基本原理及应用,包括假设函数、代价函数、梯度下降法等核心概念,同时介绍了线性和非线性边界,以及如何通过梯度下降法求解最优参数。
本文详细解析了Logistic回归的基本原理及应用,包括假设函数、代价函数、梯度下降法等核心概念,同时介绍了线性和非线性边界,以及如何通过梯度下降法求解最优参数。




































 5085
5085

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








