logistic回归算法

目录

1.logistic 回归算法 

2.决策边界

3.如何选择参数

4.简化代价函数与梯度下降

5.高级优化

6.实现logistic回归算法

---

1.logistic 回归算法 

logistic回归算法：针对y值是离散值的分类问题，是一种分类算法，用在标签y为离散值0或1的情况下

在定义假设函数时，要使用到logistic函数或者说是sigmoid函数，这两个术语的意思是一样的，下图所示假设函数定义：

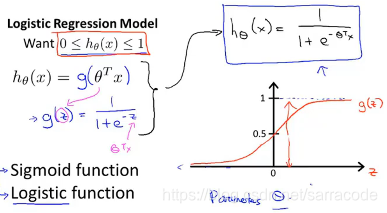
那么有了假设函数以后，我们需要用参数拟合我们的数据，那么假设函数的输出是什么呢，如下所示：

比方说我们使用肿瘤分类的例子，那么上图中假设函数的输出的通俗解释是，在给定x的条件下y=1的概率，即病人的特征为x的情况下，x是病人肿瘤的大小，这个概率的参数是，然后可以依赖假设来估计y=1的概率。

2.决策边界

那么，我们可以有前面的假设函数式子以及图像得出一个结论，就是如果（相当于z）>=0,由图像可知，h（）>=0.5，那么

我们就认为y=1。

现在假设有一个训练集，如下图所示，x1+x2=3这条线就称为决策边界，这个是线性的