Word2Vec学习笔记（四）——Negative Sampling 模型

    前面讲了Hierarchical softmax 模型，现在来说说Negative Sampling 模型的CBOW和Skip-gram的原理。它相对于Hierarchical softmax 模型来说，不再采用huffman树，这样可以大幅提高性能。

一、Negative Sampling

    在负采样中，对于给定的词$w$,如何生成它的负采样集合$NEG(w)$呢？已知一个词$w$,它的上下文是$context(w)$,那么词$w$就是一个正例，其他词就是一个负例。但是负例样本太多了，我们怎么去选取呢？在语料库$\mathcal{C}$中，各个词出现的频率是不一样的，我们采样的时候要求高频词选中的概率较大，而低频词选中的概率较小。这就是一个带权采样的问题。
设词典$\mathcal{D}$中的每一个词$w$对应线段的一个长度：
$$len(w)=\frac{counter(w)}{{\sum }_{u\in \mathcal{D}}counter(u)}(1)$$
式(1)分母是为了归一化，Word2Vec中的具体做法是：记$l_0=0,l_k={\sum }_{j=1}^{k}len(w_j),k=1,2,\dots ,N$,其中，$w_j$是词典$\mathcal{D}$中的第$j$个词，则以{lj}j=0N\{l_j\}_{j=0}^{N}{lj​}j=0N​为点构成了一个在区间[0,1]非等距离的划分。然后再加一个等距离划分，Word2Vec中选取$M=10^8$，将M个点等距离的分布在区间[0,1]上，这样就构成了M到I之间的一个映射，如下图所示：

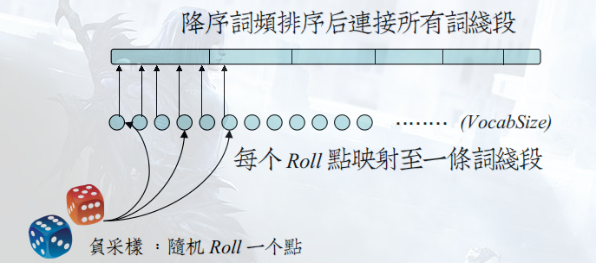
图例参考：http://www.cnblogs.com/neopenx/p/4571996.html ，建议大家读下这篇神作。

    选取负例样本的时候，取$[M_0,M_{m-1}]$上的一个随机数，对应到I上就可以了。如果对于词$w_i$,正好选到它自己，则跳过。负例样本集合$NEG(w)$的大小在Word2Vec源码中默认选5.

二、CBOW

    假定关于词$w$的负例样本$NEG(w)$已经选出,定义标签$L$如下,对于 $\forall \tilde{w}\in \mathcal{D}$：
$$L^w(\tilde{w})=\{\begin{array}{ll}1,& \tilde{w}=w;\\ 0,& \tilde{w}\ne w;\end{array}$$
对于给定的一个正例样本$(context(w),w)$, 要求：
max⁡g(w)=max⁡∏u∈{w}∪u∈NEG(w)p(u∣context(w)) \max g(w) = \max \prod_{u \in \{w\} \cup u \in NEG(w)} p(u|context(w)) maxg(w)=maxu∈{w}∪u∈NEG(w)∏​p(u∣context(w))
其中，
$$p(u|context(w))=\{\begin{array}{ll}\sigma ({\mathbf{x}}_w^T{\theta }^u),& L^w(u)=1\\ 1-\sigma ({\mathbf{x}}_w^T{\theta }^u),& L^w(u)=0\end{array}$$
把它写成一个式子：
$$p(u|context(w))=\sigma ({\mathbf{x}}_w^T{\theta }^u{)}^{L^w(u)}+(1-\sigma ({\mathbf{x}}_w^T{\theta }^u){)}^{1-L^w(u)}$$
下边解释为什么要最大化$g(w)$，
g(w)=∏u∈{w}∪u∈NEG(w)p(u∣context(w))=∏u∈{w}∪u∈NEG(w)σ(xwTθu)Lw(u)+(1−σ(xwTθu))1−Lw(u)=σ(xwTθw)∏u∈NEG(w)(1−σ(xwTθu)) g(w) = \prod_{u \in \{w\} \cup u \in NEG(w)} p(u|context(w)) \\ =\prod_{u \in \{w\} \cup u \in NEG(w)} \sigma(\boldsymbol{x}_w^T \theta^u)^{L^w(u)} + (1-\sigma(\boldsymbol{x}_w^T \theta^u))^{1-L^w(u)} \\ =\sigma(\boldsymbol{x}_w^T \theta^w)\prod_{u \in NEG(w)} (1-\sigma(\boldsymbol{x}_w^T \theta^u)) g(w)=u∈{w}∪u∈NEG(w)∏​p(u∣context(w))=u∈{w}∪u∈NEG(w)∏​σ(xwT​θu)Lw(u)+(1−σ(xwT​θu))1−Lw(u)=σ(xwT​θw)u∈NEG(w)∏​(1−σ(xwT​θu))
上式中连乘号前边的式子可以解释为最大化正例样本概率，连乘号后边解释为最小化负例样本概率。

同样的，针对于语料库，令:
$$\mathcal{G}=\prod _{w\in \mathcal{C}}g(w)$$
可以将上式作为整体的优化目标函数，取上式的最大似然：
L=log⁡G=∑w∈Clog⁡g(w)=∑w∈C∑u∈{w}∪u∈NEG(w)Lw(u)log⁡[σ(xwTθu]+[1−Lw(u)]log⁡[1−σ(xwTθu)] \mathcal{L} = \log\mathcal{G} = \sum_{w \in \mathcal{C}} \log g(w) \\ =\sum_{w \in \mathcal{C}} \sum_{u \in \{w\} \cup u \in NEG(w)}L^w(u)\log[\sigma(\boldsymbol{x}_w^T \boldsymbol{\theta}^u] + [1-L^w(u)] \log [1-\sigma(\boldsymbol{x}_w^T \boldsymbol{\theta}^u)] L=logG=w∈C∑​logg(w)=w∈C∑​u∈{w}∪u∈NEG(w)∑​Lw(u)log[σ(xwT​θu]+[1−Lw(u)]log[1−σ(xwT​θu)]
和之前的计算过程一样，记
$$L(w,u)=L^w(u)\log [\sigma ({\mathbf{x}}_w^T{\theta }^u]+[1-L^w(u)]\log [1-\sigma ({\mathbf{x}}_w^T{\mathbf{\theta }}^u)]$$
然后分别求：$\frac{\partial L(w,u)}{\partial {\mathbf{X}}_w}$和$\frac{\partial L(w,u)}{\partial {\mathbf{\theta }}^u}$,求解过程略过:
$$\begin{gathered} \frac{\partial L(w,u)}{\partial {\mathbf{X}}_w}=[L^w(u)-\sigma ({\mathbf{x}}_w^T{\mathbf{\theta }}^u)]{\mathbf{\theta }}^u \\ \frac{\partial L(w,u)}{\partial {\mathbf{\theta }}^u}=[L^w(u)-\sigma ({\mathbf{x}}_w^T{\mathbf{\theta }}^u)]{\mathbf{X}}_w \end{gathered}$$
则，可得到如下更新公式：
θu:=θu+η[Lw(u)−σ(xwTθu)]Xwv(w~):=v(w~)+∑u∈{w}∪u∈NEG(w)[Lw(u)−σ(xwTθu)]θu \boldsymbol{\theta}^u:=\boldsymbol{\theta}^u+\eta [L^w(u)-\sigma(\boldsymbol{x}_w^T \boldsymbol{\theta}^u)]\boldsymbol{X}_w \\ v(\boldsymbol{\widetilde{w}}):=v(\boldsymbol{\widetilde{w}}) + \sum_{u \in \{w\} \cup u \in NEG(w)} [L^w(u)-\sigma(\boldsymbol{x}_w^T \boldsymbol{\theta}^u)]\boldsymbol{\theta}^u θu:=θu+η[Lw(u)−σ(xwT​θu)]Xw​v(w):=v(w)+u∈{w}∪u∈NEG(w)∑​[Lw(u)−σ(xwT​θu)]θu
其中， $\tilde{\mathbf{w}}\in context(w)$.