【数控系统】第八章 七段式加减速算法

加减速算法根据分区数量可分为三段式加减速、五段式加减速、七段式加减速等，具体可查看【数控系统】第六章 加减速控制算法

本章介绍七段式加减速算法的计算流程，适用于非对称七段式加减速。（三段式和五段式的算法思路类似，在初始和结束速度均为0的情况下，计算公式更简单，这里不做赘述。）

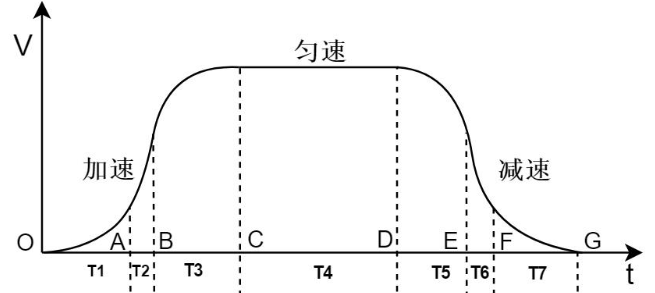
一、七段式加减速算法流程

1、方法一

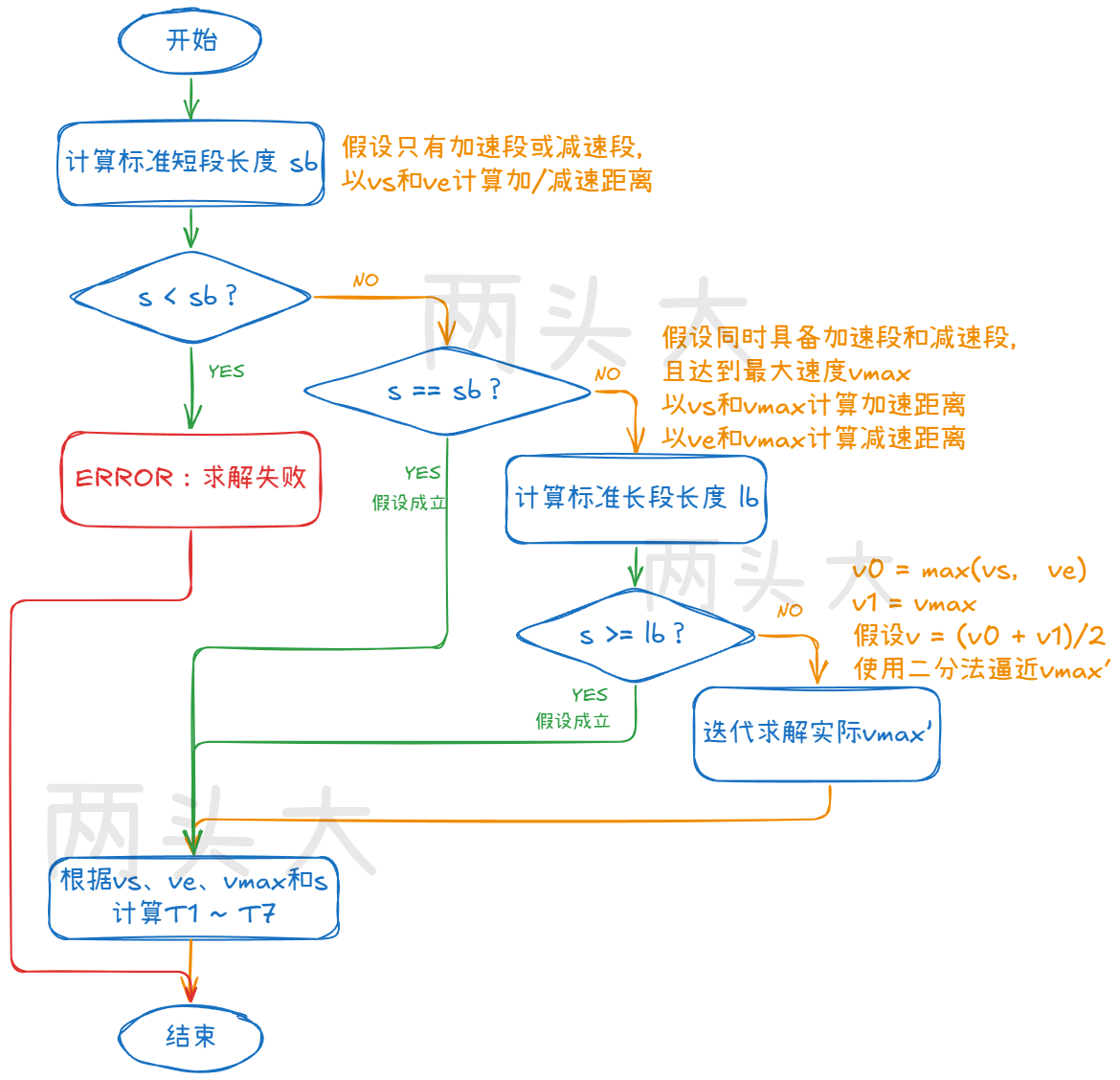
2、方法二

该方法参考《加加速度连续的S型加减速规划算法》（该论文存在勘误，请注意甄别）以及 YuZhi 在github上的开源项目 MatlabRobotAlg 。

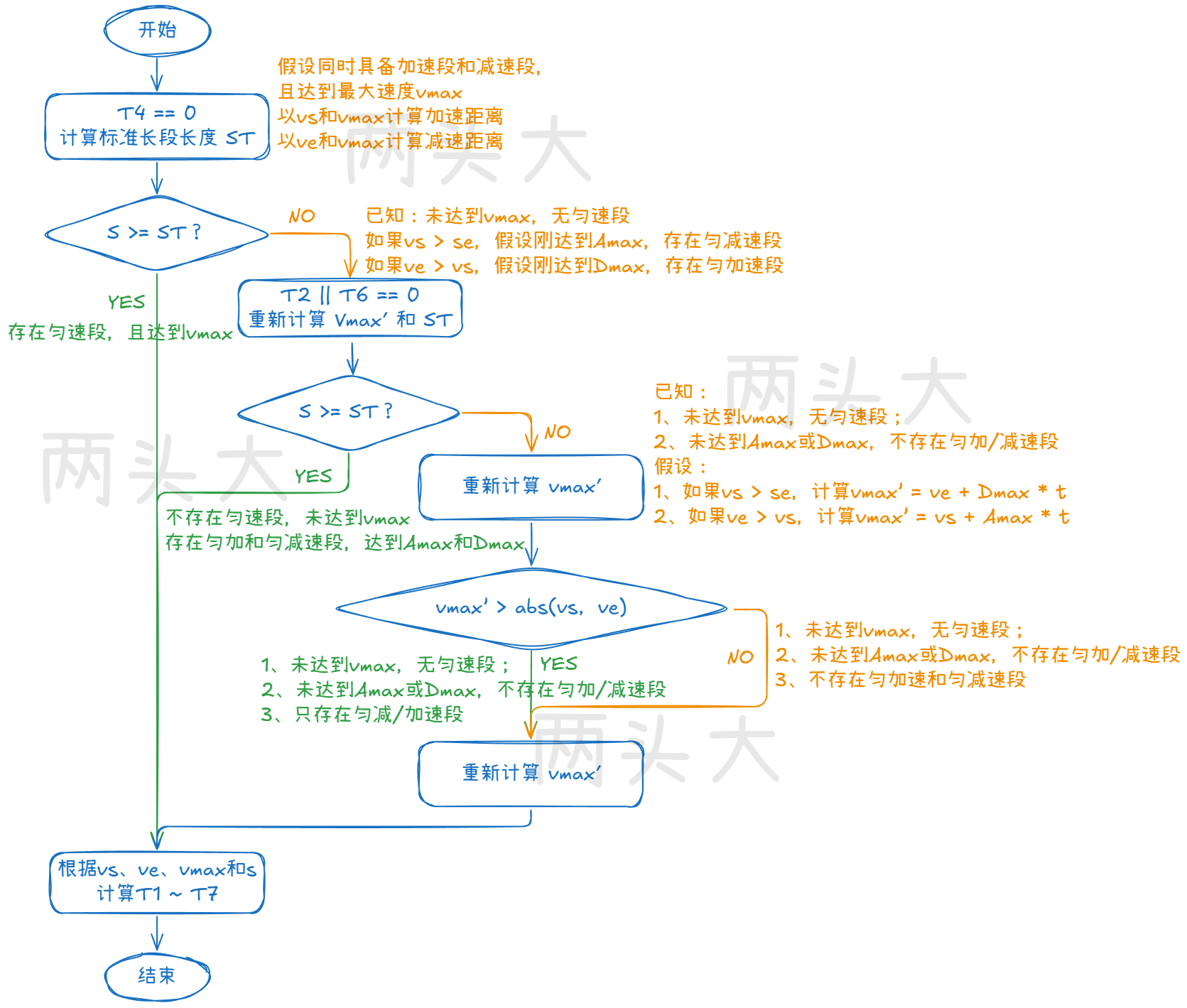
3、方法三

该方法参考《加加速度连续的S型加减速规划算法》（该论文存在勘误，请注意甄别）。

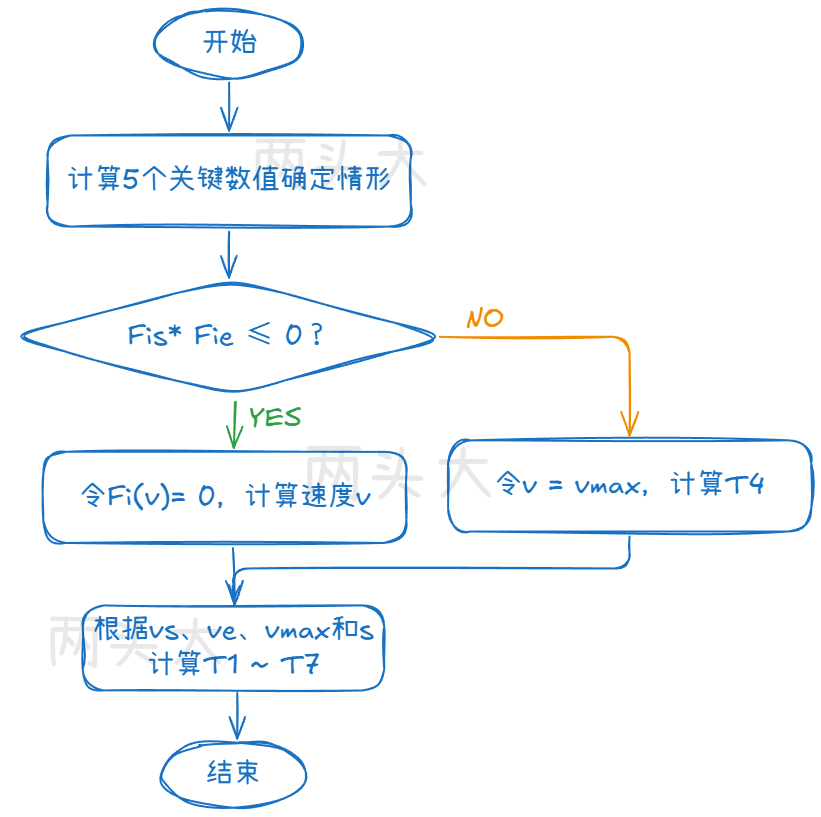
二、加减速轨迹计算

当求解出七段的时间T1~T7后，我们可以根据时间区间判断当前处于哪种状态（加加速段、匀加速度段、减加速度段、匀速段、加减速段、匀减速段、减减速段），计算当前周期的加加速度J(i)、加速度A(i)、速度V(i)和距离S(i)。

1、常规轨迹计算

采用 MatlabRobotAlg 项目进行测试，该项目为YuZhi 在 github 上的开源项目，支持T型、sin型、S型等加减速算法。

由于T(i) 为浮点数（不一定为插补周期的整数倍），因此常规轨迹计算通过判断当前周期t与T(i) 的差值是否小于阈值TOL，若是则为 T(i-1) 到 T(i) 区间。此外，由于t - T(7) 可能大于 TOL，因此需要对这种情况进行特殊判断。

① 常规轨迹计算还需考虑 t ＜ 插补周期（如1ms~8ms）的情况。在这种情况下，以上的判断逻辑会导致计算错误。

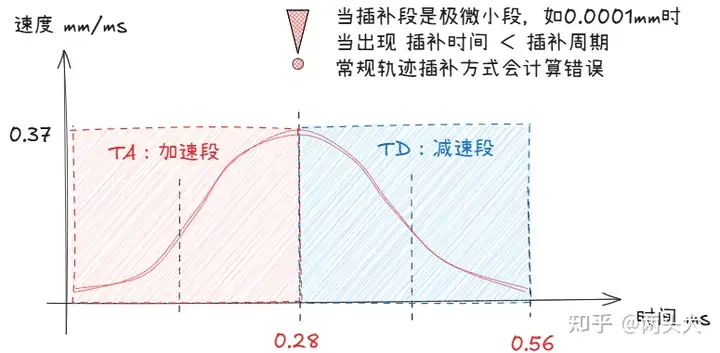
② 常规轨迹计算还需考虑 t - T(7) ＞ TOL 时，此时加加速度、加速度、速度和距离的计算方式，如果仍采用 t - T(7) ≤ TOL的方式，将会导致超出目标距离；如果直接将目标距离作为最后一个插补周期的目标位置，则会导致速度的突变。

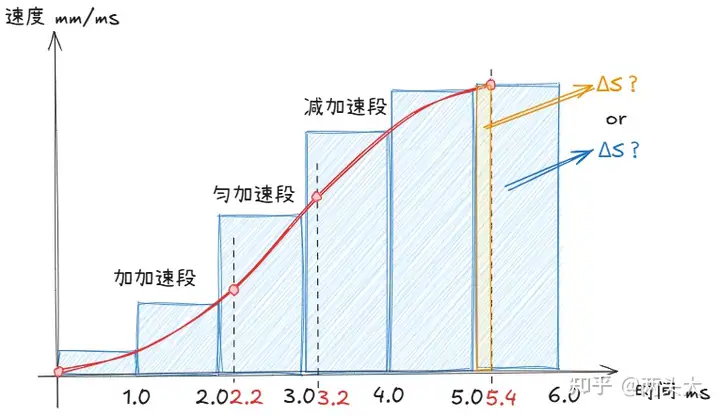
以MatlabRobotAlg 的S型加减速为例，常规轨迹计算代码如下：

function [s,v,a,jerk] = s_curve_cal_pvaj_con_ext(t,j,t_int)

    T = 0.0:t_int:t(7);
    sum_no = length(T);
    
    a = linspace(0,0,sum_no);
    v = linspace(0,0,sum_no);
    s = linspace(0,0,sum_no-1);
    jerk = linspace(0,0,sum_no);

    
    delta_t = linspace(0,0,7);
    delta_t(1) = t(1)-0.0;
    delta_t(2) = t(2)-t(1);
    delta_t(3) = t(3)-t(2);
    delta_t(4) = t(4)-t(3);
    delta_t(5) = t(5)-t(4);
    delta_t(6) = t(6)-t(5);
    delta_t(7) = t(7)-t(6);
    
    am = j*t(1);
    v1 = 1/2*j*delta_t(1)^2;
    v2 = v1+am*delta_t(2);
    v3 = v2+am*delta_t(3)-1/2*j*delta_t(3)^2;
    v4 = v3;
    v5 = v4-1/2*j*delta_t(5)^2;
    v6 = v5-am*delta_t(6);

    s1 = 1/6*j*delta_t(1)^3;
    s2 = s1+v1*delta_t(2)+1/2*am*delta_t(2)^2;
    s3 = s2+v2*delta_t(3)+1/2*am*delta_t(3)^2-1/6*j*delta_t(3)^3;
    s4 = s3+v3*delta_t(4);
    s5 = s4+v4*delta_t(5)-1/6*j*delta_t(5)^3;
    s6 = s5+v5*delta_t(6)-1/2*am*delta_t(6)^2;
    
    
    for i = 1:sum_no
%        abs(i*t_int-t(1))
       if (i*t_int >= 0) && ((i*t_int-t(1))<=0.0000001)
           temp_t = i*t_int;
           jerk(i) = j;
           a(i) = j*temp_t;
           v(i) = 1/2*j*temp_t^2;
           s(i) = 1/6*j*temp_t^3;
       elseif (i*t_int-t(2))<=0.0000001
           temp_t = i*t_int-t(1);
           jerk(i) = 0;
           a(i) = am;
           v(i) = v1+am*temp_t;
           s(i) = s1+v1*temp_t+1/2*am*temp_t^2;
       elseif (i*t_int-t(3))<=0.0000001
           temp_t = i*t_int-t(2);
           jerk(i) = -j;
           a(i) = am-j*temp_t;
           v(i) = v2+am*temp_t-1/2*j*temp_t^2;
           s(i) = s2+v2*temp_t+1/2*am*temp_t^2-1/6*j*temp_t^3;
       elseif (i*t_int-t(4))<=0.0000001
           temp_t = i*t_int-t(3);
           jerk(i) = 0;
           a(i) = 0;
           v(i) = v3;
           s(i) = s3+v3*temp_t;
       elseif (i*t_int-t(5))<=0.0000001
           temp_t = i*t_int-t(4);
           jerk(i) = -j;
           a(i) = -j*temp_t;
           v(i) = v4-1/2*j*temp_t^2;
           s(i) = s4+v4*temp_t-1/6*j*temp_t^3;
       elseif (i*t_int-t(6))<=0.0000001
           temp_t = i*t_int-t(5);
           jerk(i) = 0;
           a(i) = -am;
           v(i) = v5-am*temp_t;
           s(i) = s5+v5*temp_t-1/2*am*temp_t^2;
       elseif (i*t_int-t(7))<=0.0000001
            temp_t = i*t_int-t(6);
            jerk(i) = j;
            a(i) = -am+j*temp_t;
            v(i) = v6-am*temp_t+1/2*j*temp_t^2;
            s(i) = s6+v6*temp_t-1/2*am*temp_t^2+1/6*j*temp_t^3;
       else
            temp_t = t(7)-t(6);
            jerk(i) = 0;
            a(i) = 0;
            v(i) = 0;
            s(i) = s6+v6*temp_t-1/2*am*temp_t^2+1/6*j*temp_t^3;
       end 
    end  

end

2、圆整轨迹计算

数控系统以固定的插补周期向伺服驱动器发送脉冲数据，一般插补周期为1~8ms（根据不同性能和型号有所不同）。因此速度和位置都是处理成插补周期的整数倍进行计算，存在离散误差。为了保证速度平稳以及确保末端位置精准，需对计算误差进行补偿。离散化后需重新计算加加速度J和加速度A。根据新的加加速度J和加速度A，计算圆整误差，并根据误差模型补偿回每个插补周期，最终实现精确的插补。

三、加减速算法可视化

1、非圆整轨迹计算

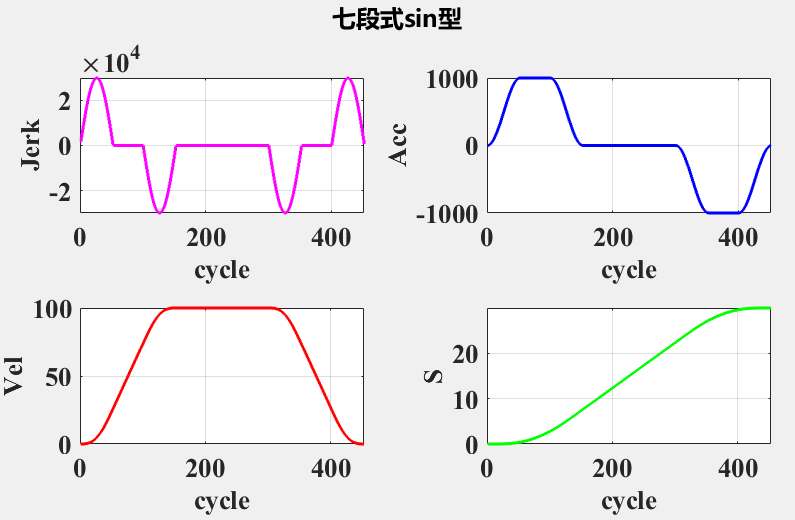
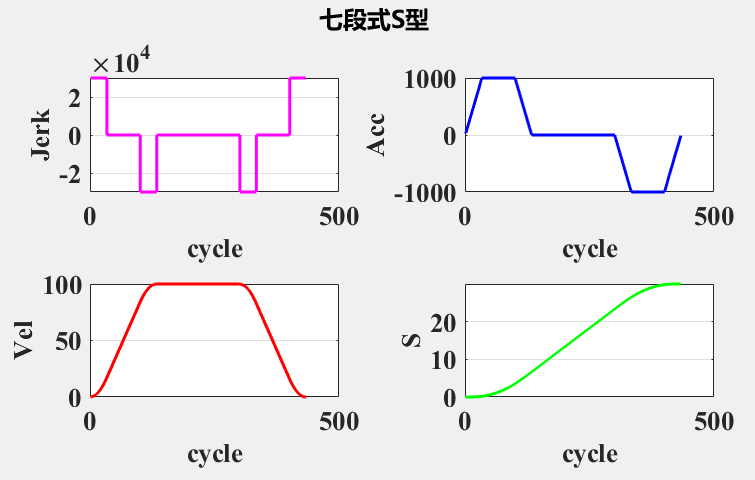
使用以下参数进行计算

% 机床参数 mm/s mm/s^2 mm/s^3 s
mac_param = struct('max_vel',100,'max_acc',1000,'max_jerk',30000,'cycle_time',0.001);

% 线段参数 mm mm/s mm/s
line_param = struct('length',30,'vs',0,'ve',0);

计算得到 t1 ~ t7 的数值，此时数值可能非插补周期1ms的整数倍，采用 YuZhi 在 github 上的开源项目 MatlabRobotAlg 中的 xx_cal_pvaj 轨迹计算函数进行显示（该项目仅支持初始速度和结束速度为0的加减速算法）。

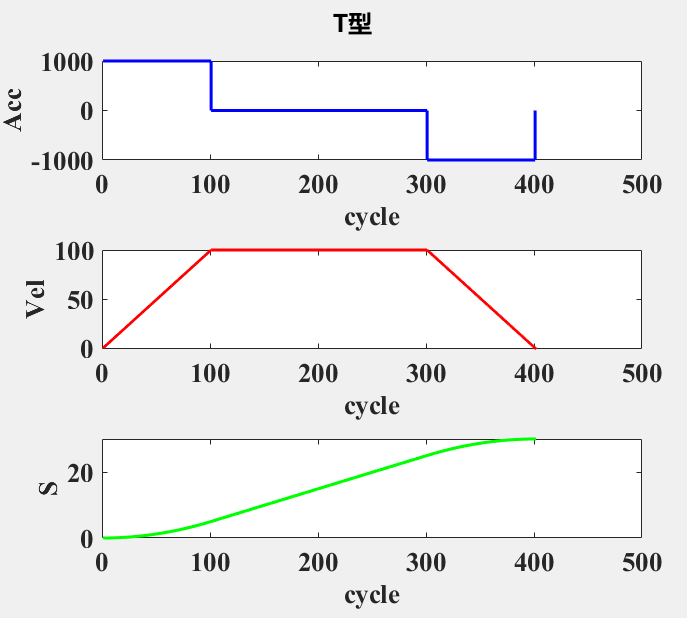
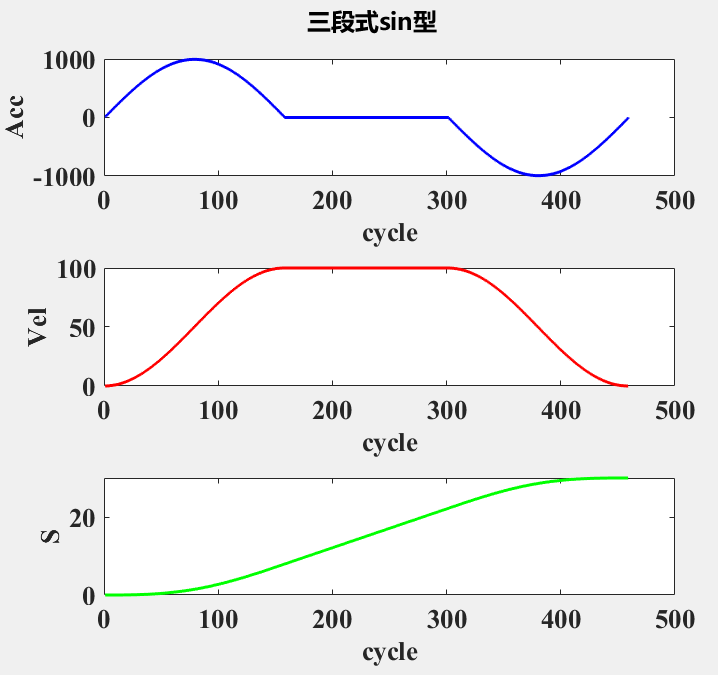
2、圆整轨迹计算

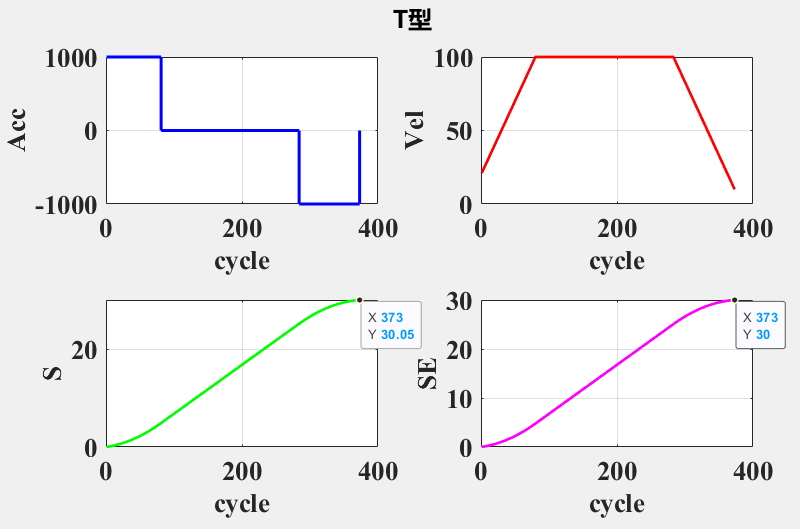
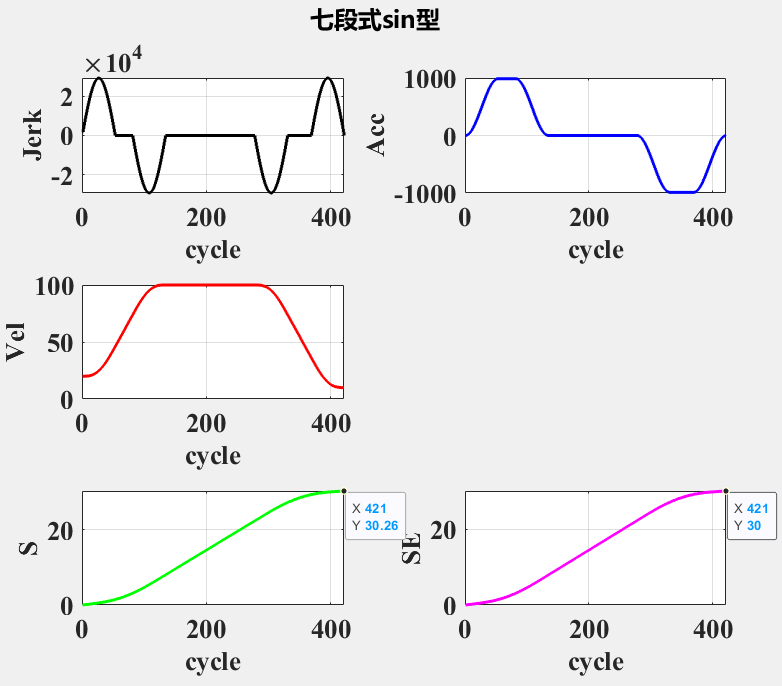
使用以下参数进行计算

% 机床参数 mm/s mm/s^2 mm/s^3 s
mac_param = struct('max_vel',100,'max_acc',1000,'max_jerk',30000,'cycle_time',0.001);

% 线段参数 mm mm/s mm/s
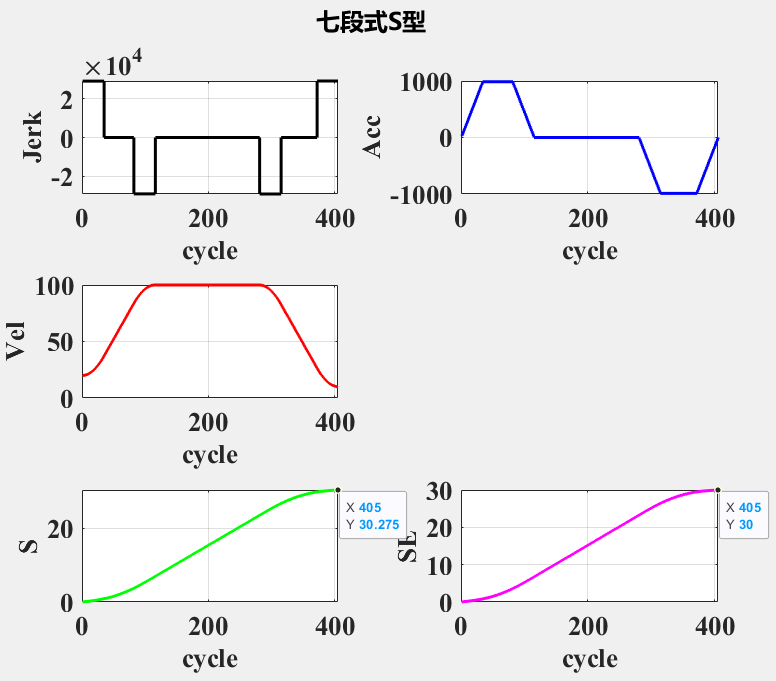
line_param = struct('length',30,'vs',20,'ve',10);

计算得到 T1 ~ T7 的数值，此时数值为插补周期1ms的整数倍，对离散后的数值进行误差补偿，得到补偿前S和补偿后SE。