手撕红黑树 C 代码

原创 已于 2025-08-16 16:59:47 修改 · 395 阅读 · 6 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #红黑树 #c语言

于 2025-08-16 16:06:51 首次发布

文章目录


持续更新中
持续更新中
持续更新中

一、插入

1、确定插入的新节点颜色

  • 黑色
    • 无论父节点是什么颜色，都会破坏 “任一节点到其所有后代外部节点的简单路径上，黑色节点的数量都相同” 这一性质
  • 红色
    • 如果父节点是红色，会破坏 “根节点到所有外部节点的简单路径上，没有两个连续的红色节点” 这一性质
    • 如果父节点是黑色，插入新节点后仍是红黑树，不需要调整

综上，插入红黑树的新节点都是红色的

2、调整不平衡的红黑树

  • 插入的新节点是根节点：直接将红色改为黑色即可
  • 插入的新节点不是根节点，并且其父节点是红色的失衡情况如下：
    • LLr
    • LLb
    • LRr
    • LRb
    • RLr
    • RLb
    • RRr
    • RRb

2.1、详解 8 种失衡

2.1.1、LLr

在这里插入图片描述
其中，x 是插入的新节点，px 是 x 的父节点，ux 是 x 的叔叔节点，gx 是 x 的祖父节点

LLr：

  • 第一个 L：插入的新节点的父节点是 gx 的左孩子
  • 第二个 L：插入的新节点是 px 的左孩子
  • r：插入的新节点的叔叔节点是红色的
2.1.2、LLb

在这里插入图片描述
其中，x 是插入的新节点，px 是 x 的父节点，ux 是 x 的叔叔节点，gx 是 x 的祖父节点

LLb：

  • 第一个 L：插入的新节点的父节点是 gx 的左孩子
  • 第二个 L：插入的新节点是 px 的左孩子
  • r：插入的新节点的叔叔节点是黑色的
2.1.3、LRr

在这里插入图片描述
其中，x 是插入的新节点，px 是 x 的父节点，ux 是 x 的叔叔节点，gx 是 x 的祖父节点

LRr：

  • L：插入的新节点的父节点是 gx 的孩子
  • R：插入的新节点是 px 的右孩子
  • r：插入的新节点的叔叔节点是红色的
2.1.4、LRb

在这里插入图片描述
其中，x 是插入的新节点，px 是 x 的父节点，ux 是 x 的叔叔节点，gx 是 x 的祖父节点

LRb：

  • L：插入的新节点的父节点是 gx 的左孩子
  • R：插入的新节点是 px 的右孩子
  • b：插入的新节点的叔叔节点是黑色的
2.1.5、RLr

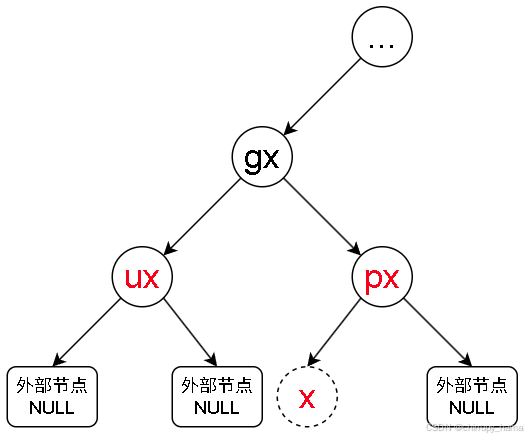
在这里插入图片描述

2.1.6、RLb

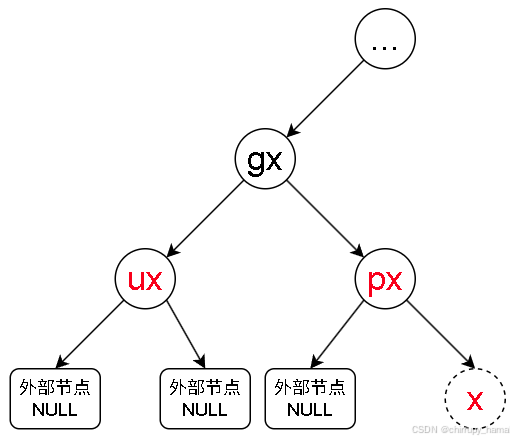
在这里插入图片描述

2.1.7、RRr

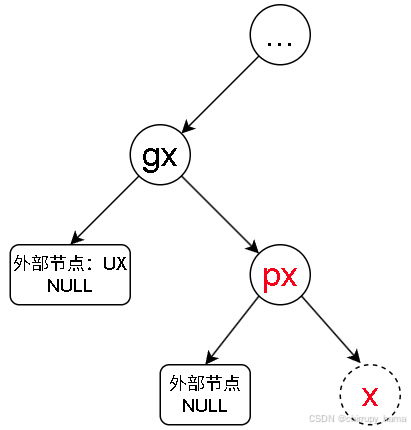
在这里插入图片描述

2.1.8、RRb

在这里插入图片描述

2.2、平衡方法

2.2.1、LXr(LLr + LRr)

以 LLr 为例
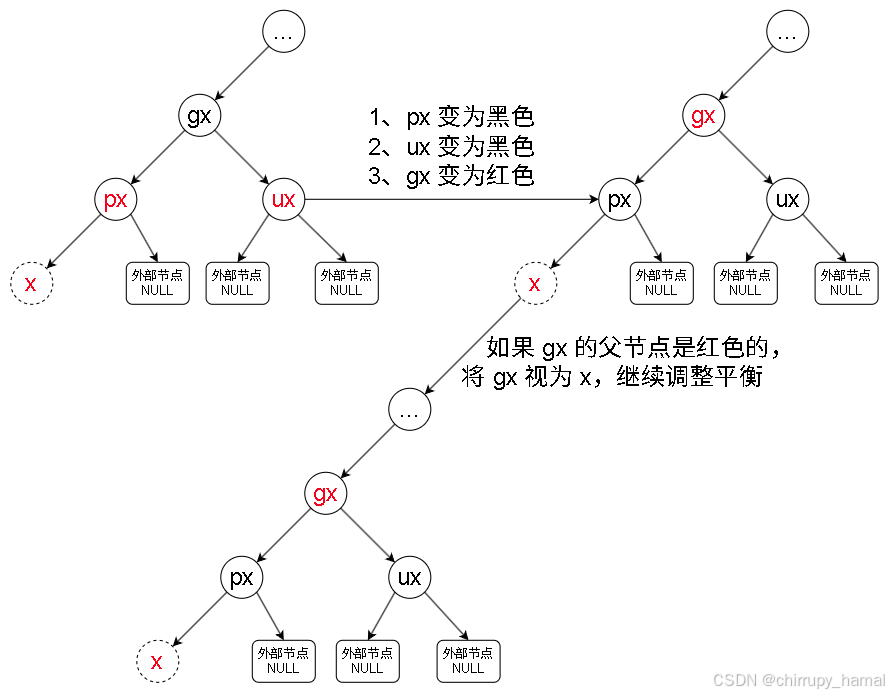
在这里插入图片描述

2.2.2、LLb

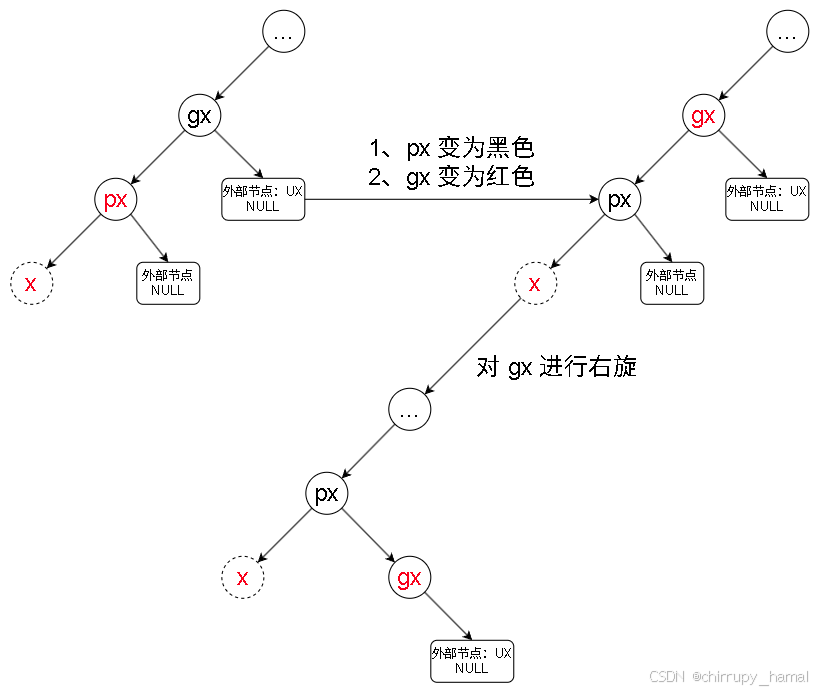
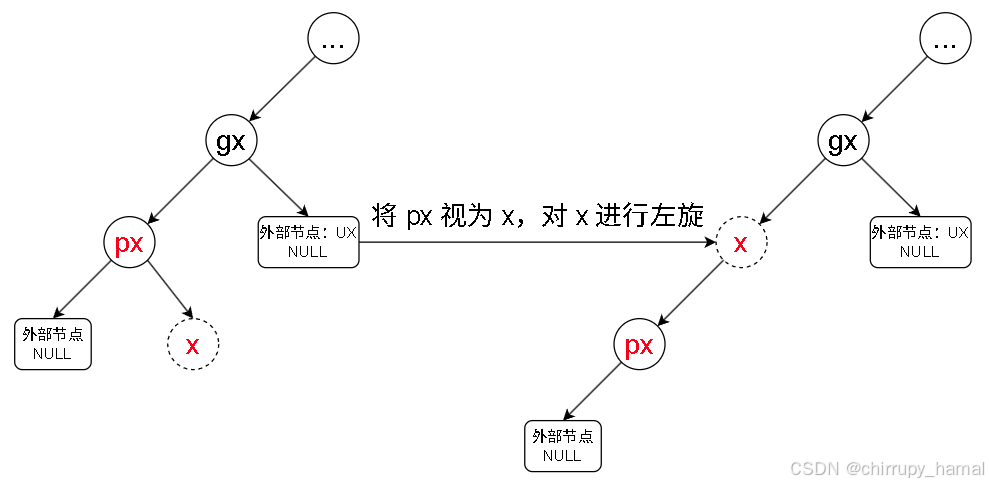
在这里插入图片描述

2.2.3、LRb

先将 LRb 变为 LLb，再按照 LLb 的操作调整平衡
在这里插入图片描述

保姆级别带你手撕红黑树BRTree
我的学习笔记分享
04-20 1884
一、前言 本文是自己在学习过程中，记录下的一些总结，以便日后复习，同时分享出来，方便与更多人学习交流，共同进步。鄙人水平有限，若有误，请不吝赐教😁😁😁。 二、从头介绍 红黑树树是一种二叉树，比较常用的数据结构，如果对二叉树不是很熟悉或者有遗忘的朋友，可以看看我之前做的笔记。 第一篇介绍二叉树的基础知识：数据结构与算法 树_振予的博客-优快云博客 第二篇介绍二叉搜索树和二叉平衡树树：数据结构与算法 查找_振予的博客-优快云博客 三、红黑树介绍 每当我们打开电脑查找一个文档、在教务系统输入我们
【手撕红黑树 | 史上最详细注解】增删查改 原理剖析 代码实现
土味儿
09-14 329
1、基本特征 红黑树起源于2-3-4树(或2-3树)，底层是二叉查找树，除二叉树的特性外，还有5大特性： 根是黑色 节点是黑色或红色 叶子节点都是黑色 叶子节点为NIL节点，不可忽略，见下图 每个红色节点的两个子节点必须是黑色 从每个叶子到根的路径上不能有两个连续的红节点 黑色平衡 从任一节点到其所有叶子节点的简单路径上黑色节点数量相同 )] 2、内部节点类Node 双向链表：父 > 子 子 > 父 /** * 内部节点
【数据结构】手撕红黑树
学了就忘是正常现象
02-26 9370
红黑树和AVL树一样，因其逻辑复杂，面试时现场要求手撕就是纯纯刁难面试者。但某大厂面试官曾要求某些求职者现场手撕红黑树（我赌5毛，让面试官撕，他也撕不出来，而且你家员工上班手搓红黑树啊？），随后求职遭遇被发到网上吐槽，这便有了“手撕红黑树”的梗，也让红黑树成为了知名度最高的数据结构。（话虽如此，对于红黑树的性质、插入思想等概念还是需要掌握的）
C++手撕红黑树
分享学习的知识，记录我的技术成长道路
08-07 913
红黑树在表意上就是一棵每个节点带有颜色的二叉搜索树，并通过对节点颜色的控制，使该二叉搜索树达到尽量平衡的状态。红黑树确保没有一条路径比其他路径长两倍。和AVL树不同的是，AVL树是一棵平衡树，而红黑树可能平衡也可能不平衡(因为是尽量平衡的状态)每一次插入都对根节点置为黑操作，因为第一种情况可能导致根节点不是黑。同时对根节点置黑也并不违反三条规定。...
【C++】：红黑树深度剖析 --- 手撕红黑树！
2301_77900444的博客
07-25 3055
就是太过追求绝对平衡，比如在插入时要维护其绝对平衡，旋转次数太多，在删除时甚至有可能要一直旋转到根位置，使之性能低下。本篇文章介绍的红黑树也是一种平衡树，是通过改变节点颜色以及旋转操作，使之接近平衡。红黑树比AVL树的用途更加广泛，在一些方面效率甚至要优于AVL树，并且 map/set 的底层封装用的也是红黑树。红黑树的节点结构与AVL树的大致相同，只是AVL树中有节点的颜色，没有平衡因子。//枚举颜色RED,BLACK,_kv(kv){}
【C++】——红黑树（手撕红黑树，彻底弄懂红黑树）
m0_74092462的博客
07-26 1954
我们之前都学过ALV树，AVL树的本质就是一颗平衡二叉树，它的作用就是查找，插入和删除节点，最坏的时间复杂度都是O(logn)的，同时维护的高度差都是小于等于1的，但是也就是因为这个原因才被红黑树所替代红黑树是一种自平衡的二叉查找树，是一种高效的查找树。它是由 Rudolf Bayer 于1978年发明，在当时被称为平衡二叉 B 树(symmetric binary B-trees)。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。
【高阶数据结构】手撕红黑树（超详细版本）
qq_42996461的博客
01-08 2747
但行好事，莫问前程
红黑树代码手撕（万字）
2401_87151064的博客
05-10 966
本文介绍了红黑树的基本概念、规则及其实现方法。红黑树是一种自平衡二叉搜索树，通过颜色标记节点并遵循特定规则来维持树的平衡，相较于AVL树，它在插入操作上更具优势。文章详细阐述了红黑树的节点结构、构造、查找、高度计算、节点计数、左右子树高度计算以及中序遍历等基本操作的实现。此外，文章还讨论了红黑树的插入和删除操作，尤其是插入操作中的旋转和颜色调整策略。最后，通过测试代码验证了红黑树的实现，并指出了在实现过程中可能遇到的问题及其解决方法。整体上，本文为读者提供了一个详细的红黑树实现指南，适合初学者学习和参考。
手撕红黑树-java版
YY3710YY的博客
08-04 435
手撕红黑树-java版 红黑树的五个平衡条件 每个节点非黑即红 根节点是黑色 叶节点（即虚拟叶节点，红黑树中的叶节点指的是看不见的虚拟空节点）是黑色 如果一个节点是红色，则它的两个子节点都是黑色的 从根节点出发到所有叶节点路径上，黑色节点数量相同 红黑树最长路径是最短路径的2倍 相比于AVL树，红黑树的控制条件更加松散，为了降低在插入和删除节点后的调整次数 红黑树自平衡的三种依据 变色：节点的颜色由黑变红或者由红变黑 左旋：已某一节点作为支点（旋转节点），其右子节点变为旋转节点的父节点，右子节点的左节
手撕红黑树RedBlackTree Right？带动画的哦
热门推荐
weixin_43272605的博客
02-20 2万+
首先这篇博客花了一点时间才总结出来，肯定还有错误，希望各位读者能够小心翼翼的看。尽量理解吧，因为我自己水平也很菜哈哈。 首先红黑树是一个二叉查找树，就是加了各种限制，让他成为了一种自平衡的二叉树。首先来看看它的五大特性，这也是我们必须要牢记的，后面多次提到，但我还是会多次重复。 GO????黑????GO 树的节点要么是红色的，要么就是黑色的（这是废话，不然怎么叫红黑树） 树的根节点一定是黑色的 ...
手撕红黑树（kv模型模拟）
2201_75373858的博客
04-24 2570
本篇博客介绍红黑树结构,通过模拟红黑树的插入，来深入理解红黑树的结构以及调整规则，红黑树原理剖析，看这一篇就够了（包会）
C++进阶之路---手撕“红黑树”
顾得泉的博客
03-18 2404
本文主要对红黑树的相关知识进行了讲解。
【数据结构与算法】—— 手撕红黑树
m0_56069910的博客
08-23 512
手撕红黑树
数据结构（12）堆排序
2401_87986548的博客
12-09 771
堆排序是一种基于堆数据结构的选择排序算法，通过构建大堆（升序）或小堆（降序）实现排序。算法分为两步：首先通过向下调整算法构建初始堆（时间复杂度O(N)），然后通过反复交换堆顶与末尾元素并调整堆完成排序（时间复杂度O(N*logN)）。堆排序空间复杂度为O(1)，但不稳定。实现时需注意升序建大堆、降序建小堆的关键区别，并通过调整父子节点关系维持堆性质。典型实现包括交换函数、向下调整函数和主排序函数，通过比较和交换操作逐步完成排序。
Redis 数据结构与典型业务映射——五大结构与 Bitmap/HyperLogLog 的适配场景地图
刘珏的博客
12-09 958
Redis 数据结构的正确选择是高性能系统的关键决策。String 适合简单键值和计数器；Hash 适合对象存储和部分更新；List 提供简单队列功能；Set 保证唯一性并支持集合运算；Sorted Set 提供排序能力；Bitmap 极大优化布尔值存储；HyperLogLog 以最小内存统计海量数据；Stream 提供完整消息队列功能。在实际应用中，​没有最优结构，只有最合适的选择​。理解业务场景的本质需求，结合数据结构的特性，才能充分发挥 Redis 的性能潜力。
数据结构==布隆过滤
2401_88453083的博客
12-09 702
布隆过滤器是由 Burton Howard Bloom 在 1970 年提出的紧凑型概率型数据结构，核心目标是解决 “海量数据的存在性快速判断” 问题，本质是哈希函数 + 位图（BitSet）的组合设计，弥补了传统哈希表空间利用率低、纯位图仅支持整数存储的缺陷。核心价值：以极小的空间开销和 O (1) 的时间复杂度，实现海量元素的存在性判断（无漏判，有可控误判）；适用场景边界：仅关注 “存在性”，不关注元素的具体内容获取（无法从过滤器中提取元素本身）。
数据结构：双向链表
2301_80026293的博客
12-09 243
一个节点结构体里有next指针域和prev指针域（前驱指针域）此前我们一直指的是链表的第一个。
数据结构（9）队列的概念和实现
2401_87986548的博客
12-09 714
本文介绍了队列的基本概念和实现方法。队列是一种遵循先进先出(FIFO)原则的线性表，包含队头和队尾指针。文章详细讲解了链式队列的实现代码，包括初始化、销毁、入队、出队等操作。同时探讨了如何用两个队列实现栈的功能，以及循环队列的设计思路。循环队列通过多开一个空间解决了判空和判满问题，提供了数组实现的具体代码示例。这些数据结构在实际应用中具有重要意义，如操作系统中的生产者消费者模型就使用了循环队列的概念。
算法基础-（数据结构）
最新发布
2401_87986548的博客
12-13 452
本文介绍了单调栈的概念及其应用。单调栈是一种具有单调性（递增或递减）的栈结构，主要用于解决四种问题：寻找元素左右侧最近且比它大/小的元素。通过示例代码演示了如何实现单调递增栈和递减栈，并详细讲解了解决这四类问题的具体方法：左侧问题正序遍历，右侧问题逆序遍历；找更大元素用递减栈，找更小元素用递增栈。最后以洛谷P5788模板题为例，展示了如何用单调递减栈从右向左遍历数组，快速找到每个元素右侧第一个更大元素的下标。
杭电笔试代码模板及手撕代码技巧参考
3. 树结构：二叉树、平衡树（如AVL树）、红黑树等的定义和基本操作。 4. 散列表（哈希表）：哈希函数的设计，冲突解决策略，以及哈希表的实现。 ### 知识点四：编程规范与技巧 良好的编程习惯和技巧对于笔试代码的...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值