不同的二叉搜索树

96. 不同的二叉搜索树

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:

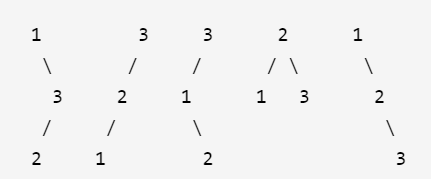
输入: 3 输出: 5 解释: 给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

题解
要构建不同的二叉树，只要根节点不同，那么一定是不同的二叉树。因此，考虑以每个数值为根节点，构建左右子树不同的二叉树，最后可以得到所有二叉树。

G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。
F(i, n): 以 i 为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。

最后需要求得：G（n）

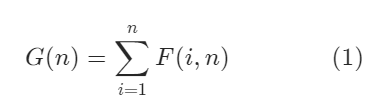
其中，G(0)=1，G(1)=1

对于以i为根节点，分为左右子树，则可以得到长度为i-1的左子树构成的不同二叉树集合，个数为G(i-1)；长度为n-i的左子树构成的不同二叉树集合，个数为G(n-i)。因此，以i为根节点的二叉树一共有的种类是左右子树的笛卡尔积，种类和是G(i-1)*G(n-i)。
因此，可得：

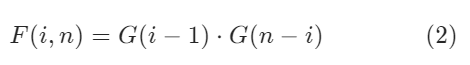
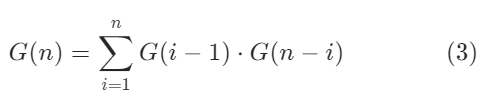
class Solution {
    public int numTrees(int n) {
        int[] G=new int[n+1];
        G[0]=1;G[1]=1;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                G[i]+=G[j-1]*G[i-j];
            }
        }   
        return G[n];
    }
}

95. 不同的二叉搜索树 II

题目
给定一个整数 n，生成所有由 1 … n 为节点所组成的 二叉搜索树 。

输入：3
输出：
[
[1,null,3,2],
[3,2,null,1],
[3,1,null,null,2],
[2,1,3],
[1,null,2,null,3]
]

整体思路和之前是一样的，只是这一道题要求具体的二叉树。
二叉树中如果求具体的二叉树构建，一般是使用递归不断查找。

class Solution {
public:
    vector<TreeNode*> generateTrees(int start, int end) {
        if (start > end) {
            return { nullptr };
        }
        vector<TreeNode*> allTrees;
        // 枚举可行根节点
        for (int i = start; i <= end; i++) {
            // 获得所有可行的左子树集合
            vector<TreeNode*> leftTrees = generateTrees(start, i - 1);

            // 获得所有可行的右子树集合
            vector<TreeNode*> rightTrees = generateTrees(i + 1, end);

            // 从左子树集合中选出一棵左子树，从右子树集合中选出一棵右子树，拼接到根节点上
            for (auto& left : leftTrees) {
                for (auto& right : rightTrees) {
                    TreeNode* currTree = new TreeNode(i);
                    currTree->left = left;
                    currTree->right = right;
                    allTrees.emplace_back(currTree);
                }
            }
        }
        return allTrees;
    }

    vector<TreeNode*> generateTrees(int n) {
        if (!n) {
            return {};
        }
        return generateTrees(1, n);
    }
};