小白也能学会的深度学习4

大家好，上篇文章我们讲了逻辑回归的模型，也知道逻辑回归的成本是很高的，我们需要去 不断的优化再优化。那我们这篇文章就来看一下怎么去优化。

2.3逻辑回归的代价函数

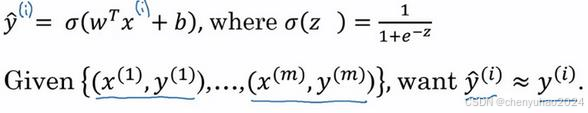
先看一下逻辑回归的输出函数，可见里面的w和b参数需要一个代价函数，通过训练代价
函数来得到。

那么如何衡量w和b的好坏呢，这就要用到我们的损失函数。

损失函数又叫做误差函数，用来衡量算法的运行情况

损失函数（Loss Function）是机器学习和深度学习中一个非常重要的概念。它用于量化模型预测值与真实值之间的差距，即模型的预测误差。通过最小化这个误差，我们可以优化模型参数，使模型在训练数据上的表现更好，并希望它在未见过的数据上也能有良好的泛化能力。

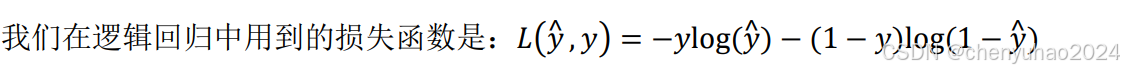
我们有了成本函数和损失函数，都是希望这两个函数的预测值尽可能的小，对于这个逻辑回归损失函数，我们也想让它尽可能地小，为了更好地理解这个损失函数怎么起作用。我们举两个例子：

实际上，我们还有很多的损失函数可以用

值得一提的是损失函数是在单个训练样本中定义的，它衡量的是算法在单个训练样本中表现如何，为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对m个样本的损失函数求和然后除以m，

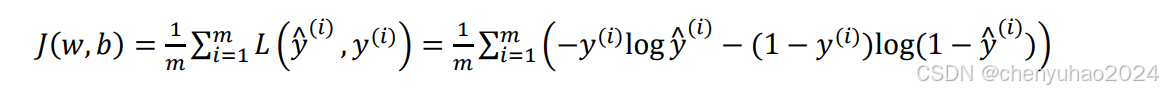
就是这样。

如果看到这里你云里雾里，没关系，后续用多了就明白了，但在这之前，我们一定要了解主线，就是推演计算的思考的整个过程。损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价。我们是通过单个训练集来对w和b进行评估，同时使得代价函数的成本尽可能的低。这就是一个非常明确的目的。

2.4 梯度下降法

梯度下降法（Gradient Descent）是一种常用的优化算法，用于最小化损失函数。通过迭代地调整模型参数，使损失函数的值逐渐减小，最终达到或接近全局最小值（在凸优化问题中）或局部最小值（在非凸优化问题中）。

梯度下降法可以做什么？

我们上面刚讲了，我们要让损失函数尽可能的小，或者说，我们要让损失函数算出来的值尽可能的靠近实际值，而且还要把我们的成本降到最低，在这里面，训练集的选择就变得至关重要了。如果选择训练集的跨度太大，那么实际上这组数据算出来的结果是没有意义的。

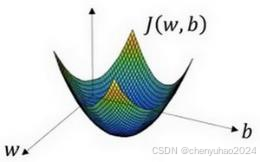
接下来就用这幅图讲一下

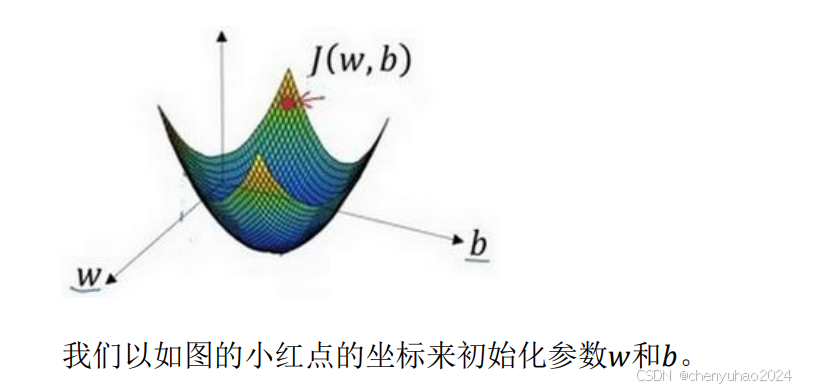
2. 朝最陡的下坡方向走一步，不断地迭代

我们朝最陡的下坡方向走一步，如图，走到了如图中第二个小红点处。

我们可能停在这里也有可能继续朝最陡的下坡方向再走一步，如图，经过两次迭代走到第三个小红点处。

3.直到走到全局最优解或者接近全局最优解的地方 通过以上的三个步骤我们可以找到全局最优解，也就是代价函数这个凸函数的最小值点。

当然这是三维的表示法，放在二维就会显得更加清晰。

实际上就是不断逼近导数的最小值的一个过程。

好了我们下篇文章见。下一篇文章，我们就会讲向量化，梯度下降的实操大家可以自己去实践，我会把代码讲一下。