接雨水问题

最新推荐文章于 2025-11-27 17:11:16 发布

原创最新推荐文章于 2025-11-27 17:11:16 发布 · 144 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#java #算法 #数据结构 #leetcode

力扣算法专栏收录该内容

83 篇文章

订阅专栏

该代码实现了一个计算数组中形成的水量的算法。通过双指针技巧，分别从数组的两端开始，找到左右两侧的最小值作为水位高度，并不断更新水位，最终累加得到总水量。在遍历过程中，若左侧元素较小，则移动左指针，反之移动右指针。同时，根据当前指针位置更新水位高度。整个过程有效地减少了时间复杂度。

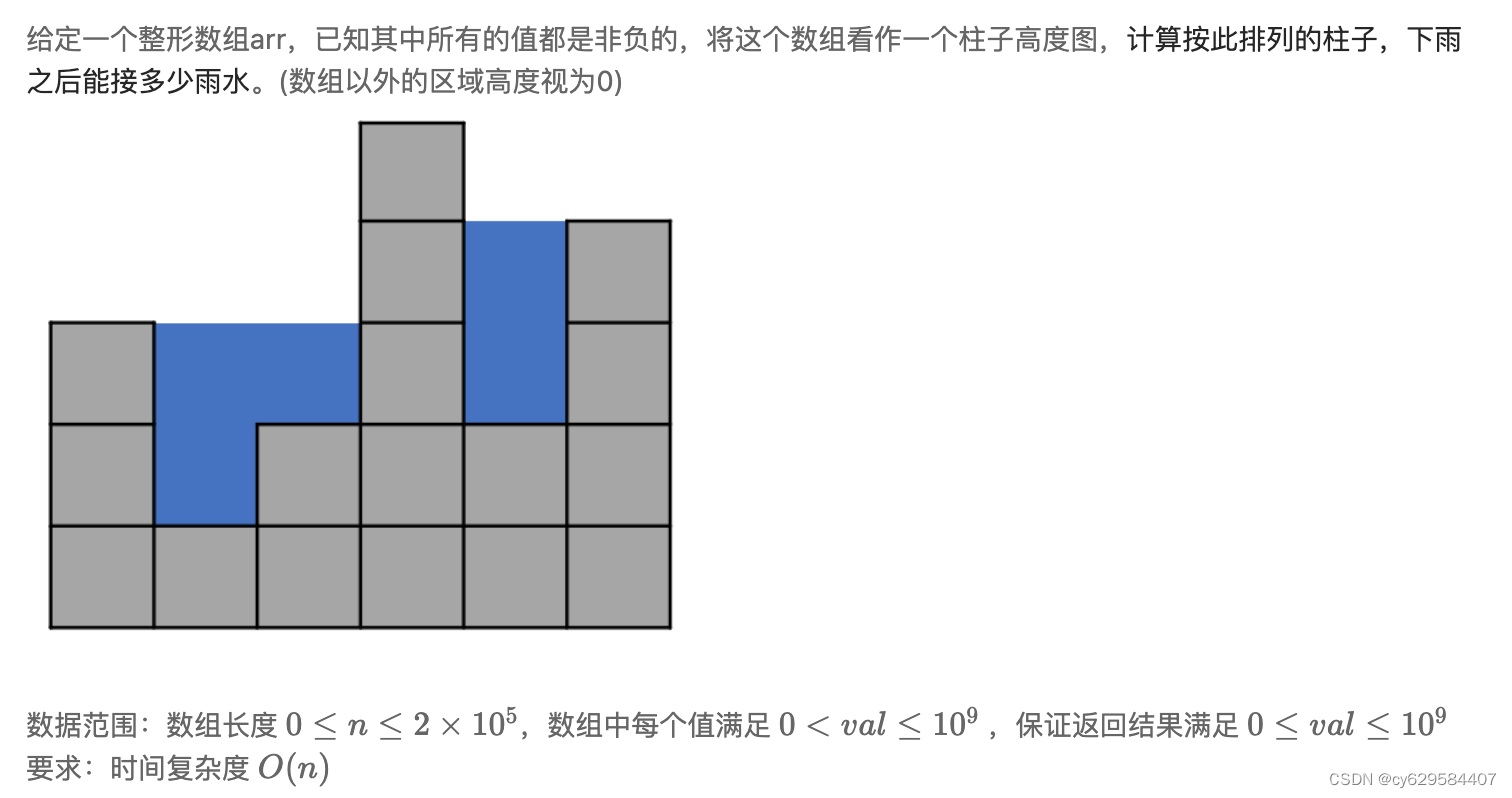
public static long maxWater(int[] arr) {
if (arr == null || arr.length <= 2) {
return 0;
}
int left = 0;
int right = arr.length - 1;
long sum = 0;
// 找出左右边界的最小值作为水位高度
int minHeight = Math.min(arr[left], arr[right]);
while (left < right) {
// 如果左边较低，则左边界向右遍历，否则右边界向左移动
if (arr[left] < arr[right]) {
left++;
// 如果当前标尺小于水位，则水量累加
if (minHeight > arr[left]) {
sum += minHeight - arr[left];
} else {
// 否则，将此标尺和右边边界高度进行比较，找出剩下数组中的新水位
minHeight = Math.min(arr[left], arr[right]);
}
} else {
right--;
// 同理，如果当前标尺小于水位，则水量累加
if (minHeight > arr[right]) {
sum += minHeight - arr[right];
} else {
// 否则，将此标尺和左边界的高度进行比较，找出剩余数组中的新水位
minHeight = Math.min(arr[left], arr[right]);
}
}
}
return sum;
}