第二周机器学习

4-2：多变量梯度下降
创建一个多变量的代价函数，这个代价函数就是建模误差的平方和


多变量线性回归的批量梯度下降算法为：

求导后：

当n>=1时，

开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

4-3：梯度下降法-特征缩放
如果两个特征的值差距悬殊的话，梯度下降法需要非常多次迭代才能收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。
最简单的方法是令： ，其中 是平均值， 是标准差。

4-4：梯度下降法-学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
梯度下降算法的每次迭代受到学习率的影响，如果学习率a过小，则达到收敛所需的迭代次数会非常高；如果学习率a过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

4-5：特征和多项式回归
有许多情况下，线性回归无法解决我们的问题，这时候可能需要曲线来适应我们的数据。
一次：

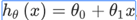
二次方模型：

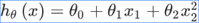
三次方模型：

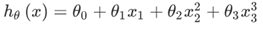
有时候可能这样更加符合：

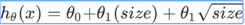4-6：正规方程
前面都是用梯度下降算法，但是针对线性回归问题，有时候，正规方程方法会更好。

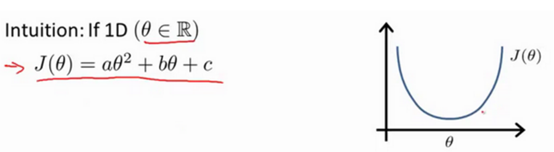
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的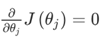： 。 假设我们的训练集特征矩阵X为 （包含了 x0=1）并且我们的训练集结果为向量 y，则利用正规方程解出向量 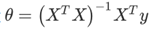。 上标T代表矩阵转置，上标-1 代表矩阵的逆。设矩阵 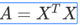，则：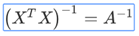

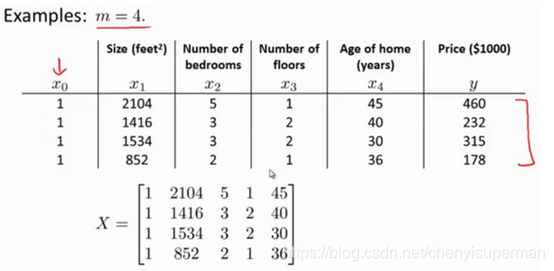
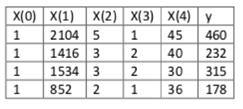
利用正规方程求解参数：

在Matlab中，正规方程写作：
pinv(X’*X)*X’*y

注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是不能用的。

梯度下降方程与正规方程的比较：

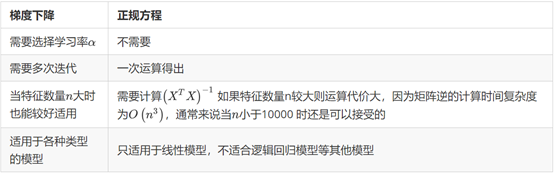
特征变量数量小于一万，可以使用标准方程法，而不使用梯度下降法。

4-7:正规方程及其不可逆性

Pinv(): 伪逆。可以展现数学上的过程，这将计算出θ 的值，即便矩阵是不可逆的。
Inv()：逆。

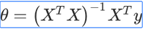的推导过程：

其中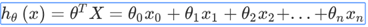
将向量表达形式转为矩阵表达形式，则有 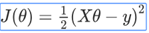，其中X为m行n列的矩阵（m为样本个数，n为特征个数），θ 为n行1列的矩阵，y为m行1列的矩阵，对J（θ） 进行如下变换:


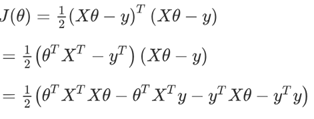
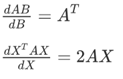
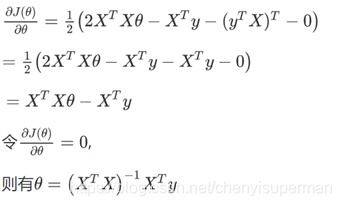
5-matlab教程
异或运算：XOR（，）

复杂的屏幕输出可以用disp()命令显示；

打印：sprintf();

V=1:0.1:2 这个集合V是一组值，从数值一开始，增量或者说是步长为0.1，直到增加到2，按照这样的方法对向量V操作，可以得到一个行向量，这是一个1行11列的矩阵，其矩阵的元素是1 1.1 1.2 1.3，依此类推，直到数值2。

V=1：6

1 2 3 4 5 6
V就被赋值了1至6的六个整数

Ones(2,3)可以生成两行三列数值都为1的矩阵

Zeros(1,3)可以生成一行三列数值都为0的矩阵

Rand(3,3)可以生成三行三列数值介于0到1之间的随机数

Hist()命令可以绘制直方图

Eye()可以绘制单位矩阵

Length()可以返回最大维度的大小

Size()可以返回数列的行数和列数

Cd ‘ ’可以改变路径，以把路径改为C:\Users\ang\Desktop，这样当前目录就变为了桌面。
Ls‘ ’ 列出我桌面上所有的路径

Load(‘ ‘)可以读入文档

Who 可以显示出在工作空间中的所有变量

Clear 加变量名  可以删除该变量 只有clear是清空所有变量

Save 文件名.类型 v可以存入硬盘，目录

A（2，:)可以返回第二行所有的元素
A（：;2）可以返回第二列所有的元素
A（	：;2）=[10;11;12]表示取出第二行，将[10;11;12]的值赋值给了它

A = [A，[100；101；102]]实际上是在原矩阵的右边附加了一个新列矩阵
A（：）就是将A里所有的元素放入一个单独的列向量

C = [A B]将两个矩阵合在了一起
C = [A;B]上下合在了一起

A.^2表示A矩阵内每一个元素平方

1./V每个元素倒数

Log(v)可以对数运算

A’就是矩阵A的转置

[Val，ind]=max(A) 这将返回矩阵A中的最大值存入val，以及该值对应的索引

max(A) ：A是一个矩阵的话，这样做就是对每一列求最大值。

Magic（） 函数将返回一个矩阵，称为魔方阵或幻方 (magic squares)，它们具有以下这样的数学性质：它们所有的行和列和对角线加起来都等于相同的值。

[r,c] = find(A>=7) 这将找出所有A矩阵中大于等于7的元素，因此， r和c分别表示行和列.

sum(a):将a中所有的元素相加。

prod(a): prod 意思是product(乘积)，它将返回这a中元素的乘积。

floor(a)：向下舍小数

ceil(a)：向上进小数，进1

max(rand(3),rand(3))：返回两个3×3的随机矩阵，并且逐元素比较取最大值。

max(A,[],1)：得到每一列的最大值；1表示取A矩阵第一个维度的最大值
max(A,[],2)：得到每一行的最大值；

max(max(A))：找出整个矩阵A的最大值；
max(A(:))：把 A当做一个向量，并返回A向量中的最大值；

sum(A,1):得到每一列的和；

flipup/flipud 表示向上/向下翻转。

print –dpng ‘myplot.png’：png是一个图像文件格式，这样输入，它可以为你保存为一个文件。

A = magic(5)

imagesc(A), 它将会绘制一个55的矩阵，一个55的彩色格图，不同的颜色对应A矩阵中的不同值。

imagesc(A)，colorbar，colormap gray , 它生成了一个颜色图像，一个灰度分布图，并在右边也加入一个颜色条。所以这个颜色条显示不同深浅的颜色所对应的值。

6-1：分类问题
逻辑回归 (Logistic Regression) 算法

6-2：假说表示
引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。 逻辑回归模型的假设是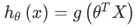： 其中： X代表特征向量 g代表逻辑函数（logistic function)是一个常用的逻辑函数为S形函数（Sigmoid function），公式为: 。

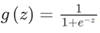Python实现：
import numpy as np

def sigmoid(z):

return 1 / (1 + np.exp(-z))

该函数的图像为：

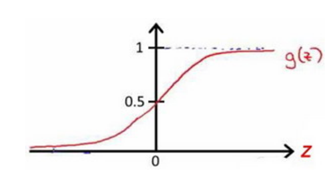
对模型的理解：
h_θ(x)的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probablity）即 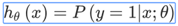例如，如果对于给定的x，通过已经确定的参数计算得出，则表示有70%的几率y为正向类，相应地为负向类的几率为1-0.7=0.3。

6-3:判定边界