前缀和技巧（C++实现）

以下内容是我在力扣上的一些提交记录，如果有不对的地方，还请指正~

---

前缀和技巧适用于快速计算一个索引区间内的元素之和。

力扣相关题目：

• 303、区域和检索-数组不可变
• 560、 和为 K 的子数组
• 304、 二维区域和检索 - 矩阵不可变

 303、区域和检索-数组不可变

题目描述：

 我的提交

需要注意的是，初始化数组需要在numarray外面，因为sumrange方法也是需要使用到这个数组的。

class NumArray {
public:
    vector<int> sum;
    NumArray(vector<int>& nums) {
        int n = nums.size();
        sum.resize(n+1);
        sum[0] = 0;
        for(int i=0; i<n; i++)
            sum[i+1] = sum[i] + nums[i];
    }
    
    int sumRange(int left, int right) {
        return sum[right+1] - sum[left];
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(left,right);
 */

560、 和为 K 的子数组

题目描述

 

我的提交

这段代码其实就是先用sum数组存储前缀和，然后根据要求的k值寻找相应的区域，并用ans进行记录，之后返回ans，即为要求的值。

但是这段代码进行了报错，是因为超时，时间复杂度是O（n^2），所以可以使用哈希表的方法：键值是某段区域的元素和，value是该元素和出现的次数。

//超时
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> sum(n+1);
        sum[0]=0;
        for(int i=0;i<n;i++){
            sum[i+1]=sum[i]+nums[i];
        }
        int ans=0;
        for(int i=1;i<=n;i++){
            for(int j=0;j<i;j++){
                if(sum[i]==sum[j]+k)
                    ans++;
            }
        }
        return ans;
    }
};

 下面是解决这道题的代码。这种解法给我的感觉有点像滑动窗口，求出前i个数的和（sum），然后找sum-k有没有在之前的前缀和里出现过。如果有，从i这个位置到之前sum-k出现的位置，这个片段之和就是k。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int len=nums.size();
        unordered_map<int,int>preSum;
        preSum[0]=1;
        int cnt=0,sum=0;
        for(int i=0;i<len;i++){
            sum+=nums[i];
            if(preSum[sum-k]!=0){
                cnt+=preSum[sum-k];
            }
            preSum[sum]++;
        }
        return cnt;
    }
};

 304、二维区域和检索 - 矩阵不可变

题目描述：

 我的提交

需要注意的点：

而且，前缀和矩阵是从preSum[1][1]开始存储的。

前缀和矩阵的生成，见代码11行，代表的是：绿色框=红色框+黄色框+蓝色框-紫色框。

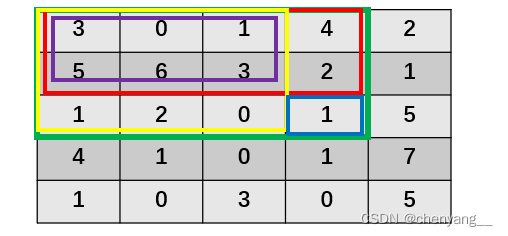
以上图为例，preSum[3][4] = preSum[2][4] + preSum[3][3] + matrix[4][4] - preSum[2][3];

前缀和矩阵生成之后，就是按照给定的左上角横纵坐标值和右下角横纵坐标值，获得给定矩阵的值。

需要注意的是，此处传入的下标值是从零开始的，而preSum是从1开始的，这也是为什么最后要获得矩阵和的时候，要将右下角的坐标值加一。

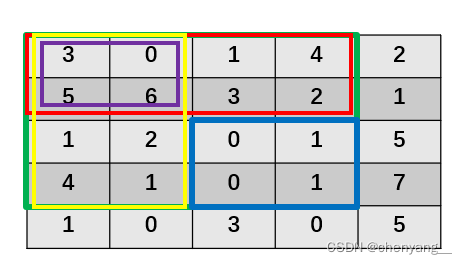
preSum[row2+1][col2+1]-preSum[row1][col2+1]-preSum[row2+1][col1]+preSum[row1][col1]

蓝色框 = 绿色框-红色框-黄色框+紫色框

class NumMatrix {
public:
    vector<vector<int>> preSum;
    NumMatrix(vector<vector<int>>& matrix) {
        int a=matrix.size(),b=matrix[0].size();
        preSum.resize(a+1,vector<int>(b+1));
        if(a==0 || b==0)
            return;
        for(int i=1; i<=a;i++){
            for(int j=1; j<=b;j++){
                preSum[i][j] = preSum[i-1][j]+preSum[i][j-1]+matrix[i-1][j-1]-preSum[i-1][j-1];
            }
        }

    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2+1][col2+1]-preSum[row1][col2+1]-preSum[row2+1][col1]+preSum[row1][col1];
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */