【算法入门06】重建二叉树

最新推荐文章于 2025-11-24 17:02:03 发布

原创

最新推荐文章于 2025-11-24 17:02:03 发布 · 812 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #c++

本文详细解析如何利用前序遍历和中序遍历重建二叉树，通过递归方法逐层构造，适用于编程挑战。核心知识点包括二叉树结构、遍历顺序理解和递归调用。

核心考点：二叉树重建，遍历理解，递归

给定某二叉树的前序遍历和中序遍历，且前序遍历和中序遍历当中无重复元素，请重建出该二叉树并返回它的头结点。例如输入前序遍历序列{1, 2, 4, 7, 3, 5, 6, 8}和中序遍历序列{4, 7, 2, 1, 5, 3, 8, 6}，则重建出的二叉树如下图所示。
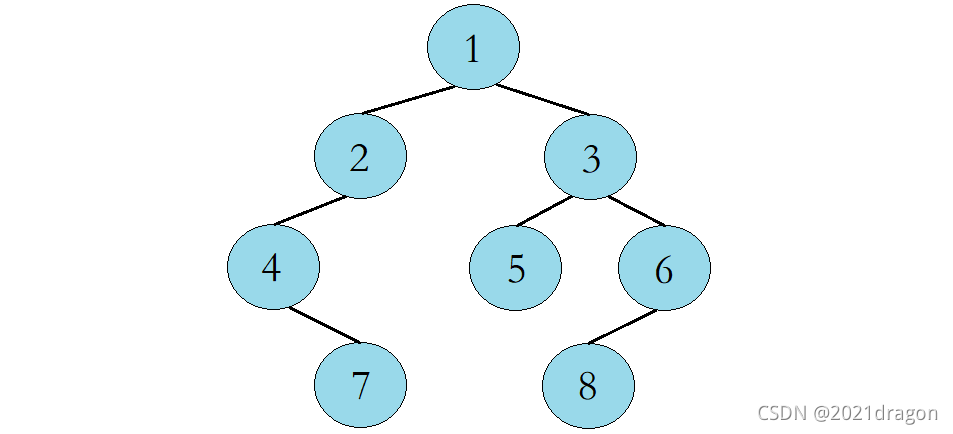
在这里插入图片描述
解析：
首先我们必须知道前序遍历和中序遍历的遍历顺序：

前序遍历顺序：根 -> 左子树 -> 右子树
中序遍历顺序：左子树 -> 根 -> 右子树

据此我们可以知道，前序遍历序列的第一个数字一定是二叉树的根结点。得到了根结点的值后，我们就可以在中序遍历当中找到根结点的位置。
在这里插入图片描述
因为中序遍历的顺序是：左子树 -> 根 -> 右子树，所以此时根结点的左边便是左子树的中序遍历序列，根结点的右边便是右子树的中序遍历序列。

而且我们还可以根据根结点在中序遍历序列当中的下标，计算出左子树的结点个数和右子树的结点个数，并据此得到左子树的前序遍历序列和右子树的前序遍历序列。
在这里插入图片描述
此时，根据前序遍历序列和中序遍历序列重建二叉树的问题就变成了，根据左子树前序遍历序列和中序遍历序列重建左子树，以及根据右子树前序遍历序列和中序遍历序列重建右子树了。而我们可以用相同的方法去进行重建，直至子树的前序序列以及中序序列不存在，此时二叉树也就重建好了。

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
   
   
public:
	TreeNode* reConstructBinaryTree(vector<