相向双指针练习

相向双指针练习

最接近的三数之和

给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。

返回这三个数的和。

假定每组输入只存在恰好一个解。

示例 1：

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2)。

示例 2：

输入：nums = [0,0,0], target = 1
输出：0
解释：与 target 最接近的和是 0（0 + 0 + 0 = 0）。

提示：

• 3 <= nums.length <= 1000
• -1000 <= nums[i] <= 1000
• -104 <= target <= 104

题目分析

这个其实和我们昨天做的三数之和是一个道理，使三数之和与target最接近其实就是求最小的|三数之和 - target|，整体的思路就是这样，所以沿用三数之和的求解思路，首先对数组排序，而后再用一个双指针，便可以得出结果了，需要注意的是，我们使用closest这个值来存储最终的结果，其思路其实类似于我们在数组中找到最小值。于是我们可以得到下面的代码。

链接: 两数之和 三数之和

leetCode代码

class Solution {
    public int threeSumClosest(int[] nums, int target) {
        int n = nums.length;
        Arrays.sort(nums);
        int closest = nums[0] + nums[1] + nums[2] - target;

        for(int i = 0; i < n - 2; i ++){
            int j = i + 1;
            int k = n - 1;
            while(j < k){
                int sum = nums[i] + nums[j] + nums[k] - target;

                if(sum == 0) return sum + target;
                if(Math.abs(closest) > Math.abs(sum)) {
                    closest = sum;
                }
                if(sum < 0) {
                    j ++;
                    while(j < k && nums[j] == nums[j - 1]) j ++;
                }
                else {
                    k --;
                    while(j < k && nums[k] == nums[k + 1]) k --;
                }
            }
        } 
        return closest + target;
    }
}

优化

优化其实也和昨天的思路一模一样，在这不进行单独说明了，大家可以把这道题作为昨天学习之后的练手。

class Solution {
    public int threeSumClosest(int[] nums, int target) {
        int n = nums.length;
        int closest = nums[0] + nums[1] + nums[2];
        Arrays.sort(nums);

        // 如果closet等于 target，直接返回
        if(closest == target) return closest;

        for(int i = 0; i < n - 2; i ++){
            // 对i去重
            if(i > 0 && nums[i] == nums[i - 1]) continue;

            // 如果当前最小的三个数相加大于target，那么后续的一定大于
            if(nums[i] + nums[i + 1] + nums[i + 2] > target) {
                if(Math.abs(closest - target) > Math.abs(nums[i] + nums[i + 1] + nums[i + 2] - target))
                    closest = nums[i] + nums[i + 1] + nums[i + 2];
                break;
            }
            // 如果当前最大的三个数相加小于target，说明需要迭代掉当前i
            if(nums[i] + nums[n - 1] + nums[n - 2] < target){
                if(Math.abs(closest - target) > Math.abs(nums[i] + nums[n - 1] + nums[n - 2] - target))
                    closest = nums[i] + nums[n - 1] + nums[n - 2];
                continue;
            }
            
            int j = i + 1;
            int k = n - 1;

            while(j < k){
                int sum = nums[i] + nums[j] + nums[k];

                if(sum == target) return target;
                if(Math.abs(closest - target) > Math.abs(sum - target)) closest = sum;

                if(sum > target){
                    k --;
                    while(j < k && nums[k] == nums[k + 1]) k --;
                }else {
                    j ++;
                    while(j < k && nums[j] == nums[j - 1]) j ++;
                }
            }
        }
        return closest;
    }
}

盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：

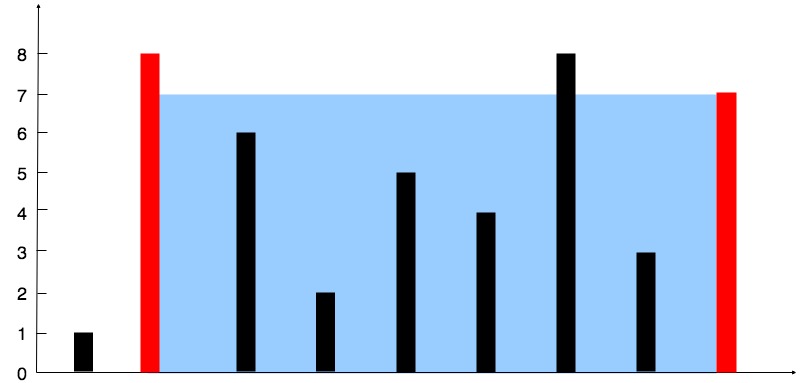
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

题目分析

本题的逻辑依然十分简单，利用相向双指针，l & r，如果比较指针对应的两条线，较短的一条为容器的高，l和r之间的距离作为容器的宽，计算完当前容器的容量之后将其存储到mArea中，而后将较短的那条线的下标向中间靠拢一位，重复上述操作，并且将得到的容量不断比较，替换，便可以得到最大的容量；

leetCode代码

class Solution {
    public int maxArea(int[] height) {
        int n = height.length;
        int l = 0, r = n - 1;
        int mArea = 0;

        while(l < r){
            int area = (r - l) * Math.min(height[l], height[r]);

            if(mArea < area) mArea = area;
            if(height[l] < height[r]) l ++;
            else r --;
        }
        return mArea;
    }
}

接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

题目分析

前后缀分解

本题可以把每个洼地都看成是宽度为1的桶，而桶的高度则取决于两个柱子中较短的柱子。所以利用前后缀最大值来分别得到对应位置左边最高的柱子高度和右边最高的柱子高度，计算时取两者中较小者与对应位置上的柱子高度之差作为该“桶”的容量即可。

代码

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        // 前缀最大值
        int[] pre_max = new int[n];
        pre_max[0] = height[0];
        for(int i = 1; i < n; i ++){
            if(height[i] > pre_max[i - 1])
            pre_max[i] = height[i];
            else
            pre_max[i] = pre_max[i - 1];
        }
        // 后缀最大值
        int[] suf_max = new int[n];
        suf_max[n - 1] = height[n - 1];
        for(int i = n - 2; i >= 0; i --){
            if(height[i] > suf_max[i + 1])
            suf_max[i] = height[i];
            else 
            suf_max[i] = suf_max[i + 1];
        }
        int sum = 0;
        for(int i = 0; i < n; i ++){
            sum += Math.min(pre_max[i], suf_max[i]) - height[i];
        }
        return sum;
    }
}

相向双指针

这个相对于前后缀的方法来说，空间复杂度会更低一点，其实就是前后缀方法的优化版本。

如同前后缀的方法啊，我们还是把洼地看成是宽度为1的桶，如果我们一开始只知道左边的前缀最大值和右边的后缀最大值，比如示例一中的height[2]，假设我们只知到第三根柱子的前缀最大值，以及后五根柱子的后缀最大值，此时对于height[2]来说，它的前置最大值为1，后缀最大值为3，由于前缀最大值不会再缩小（也就是“桶”的高度不会再缩小），所以我们可以认为height[2]这个“桶”的容量就是1 - 0 = 1。

基本思路了解，代码如下：

代码

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int left = 0; 
        int right = n - 1;
        // 使用一个数来代表前缀最大值和后缀最大值
        int pre_max = height[0], suf_max = height[n - 1];
        int sum = 0;
        while(left <= right){
            // 不断迭代前后缀最大值的
            pre_max = Math.max(height[left], pre_max);
            suf_max = Math.max(height[right], suf_max);

            if(pre_max < suf_max){
                sum += pre_max - height[left];
                left ++;
            }else{
                sum += suf_max - height[right];
                right --;
            }
        }
        return sum;
    }
}