小白练习代码准备机试（二）相向双指针解决盛水最多的容器和接雨水

       亲爱的小伙伴们大家好呀，今天我学习了灵神的基础算法精讲第二个内容，盛水最多的容器和接雨水题目，不愧是灵神呀，一下就能抓住问题的本质，让我恍然大悟，感兴趣的小伙伴一起看下去吧！

盛水最多的容器

        本题的原题： 11. 盛最多水的容器 - 力扣（LeetCode）这道题简化为数学模型可以理解为，找到里面的两条垂线使得和x轴的面积最大。我们首先明白“木桶原理”，就是指一个桶能装水的多少是由木桶最短的那块板决定的，我们随机选其中的两条线，面积就是（两线在x轴之间的距离）*（两个线中短的线的高度）。

        因此，我们还是想到了相向双指针，在最左和最右分别设置一个指针，然后计算此时的面积，用ans记录面积最大值，出现面积更大就更新ans的值，然后比较左右木板的高度，哪个木板短就向中间移动哪个。整体的c++代码如下：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n=height.size();
        //设置相向双指针
        int left=0,right=n-1;
        int area=0,ans=0;
        while(left<right)
        {
            //计算矩形面积
            area=(right-left)*min(height[left],height[right]);
            ans=max(ans,area);
            //比较，把短的板向中间移动遍历
            if(height[left]<height[right])
            left++;
            else
            right--;
        }
        return ans;
    }
};

接雨水

       下面我们来看接雨水这道题，原题42. 接雨水 - 力扣（LeetCode），我们按照两个方法来讲解。

方法一：前后缀法

       对于接雨水这道题目，我们把每个小宽度都假设成一个宽度为1的木桶，那么这个小木桶能放多少水取决于以这个桶为分界线，桶前面所有板里面最长的那个，和桶后面所有板里最长的那个。

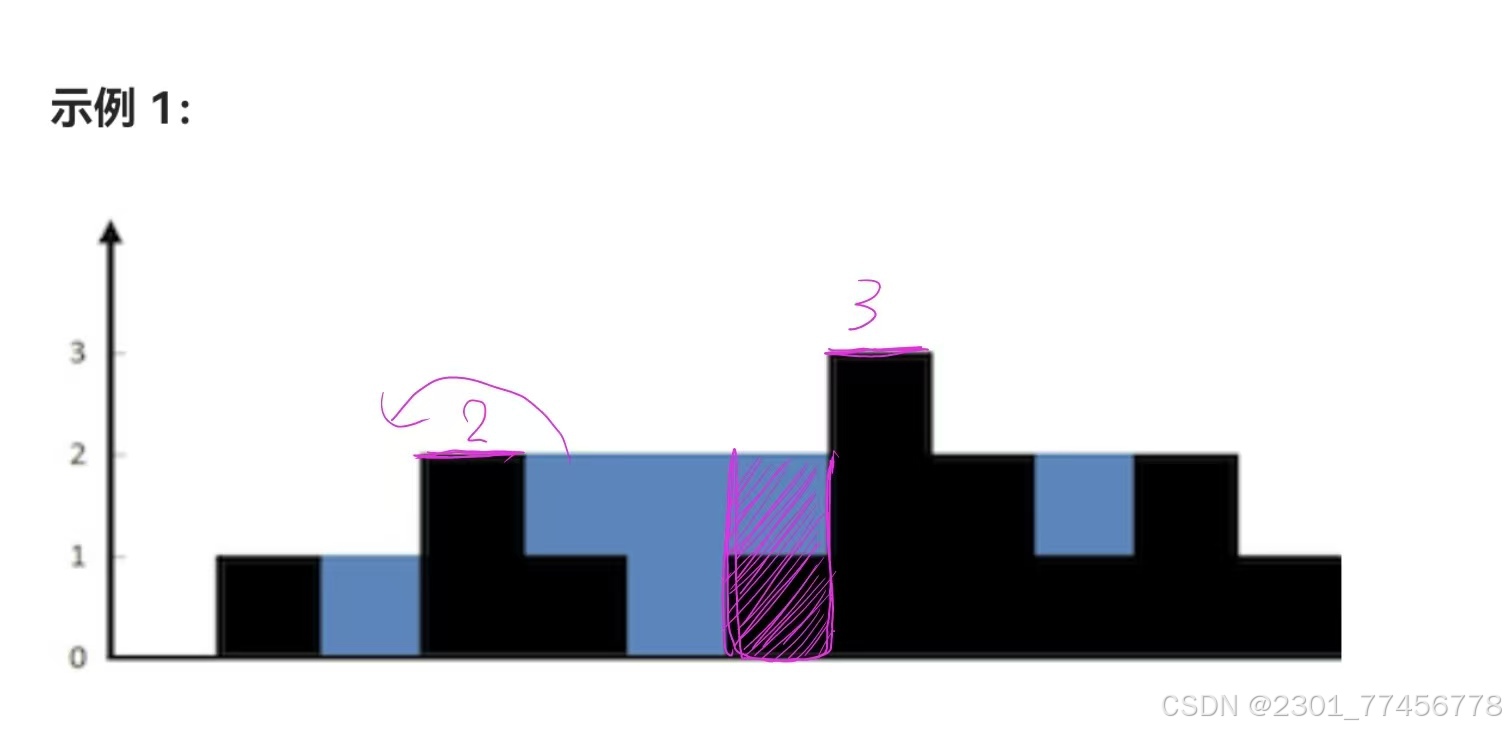
       比如上图中画斜线阴影的木桶，它左侧中最长的板应该是2，右侧中最长的板是3，他应该取决于短的那块，也就是2，再减去自己高度1，所以他能存放的雨水应该就是2-1=1。其他木桶同理，如果比短的那块高就会溢出去，比短的那块低才能存住水。

       因此，我们把木桶左边最长的板长叫做最长前缀，右边最长的板叫做最长后缀，我们可以从左往右和从右往左分别标出最长前缀和后缀。分别记作left数组和right数组，如下图所示：

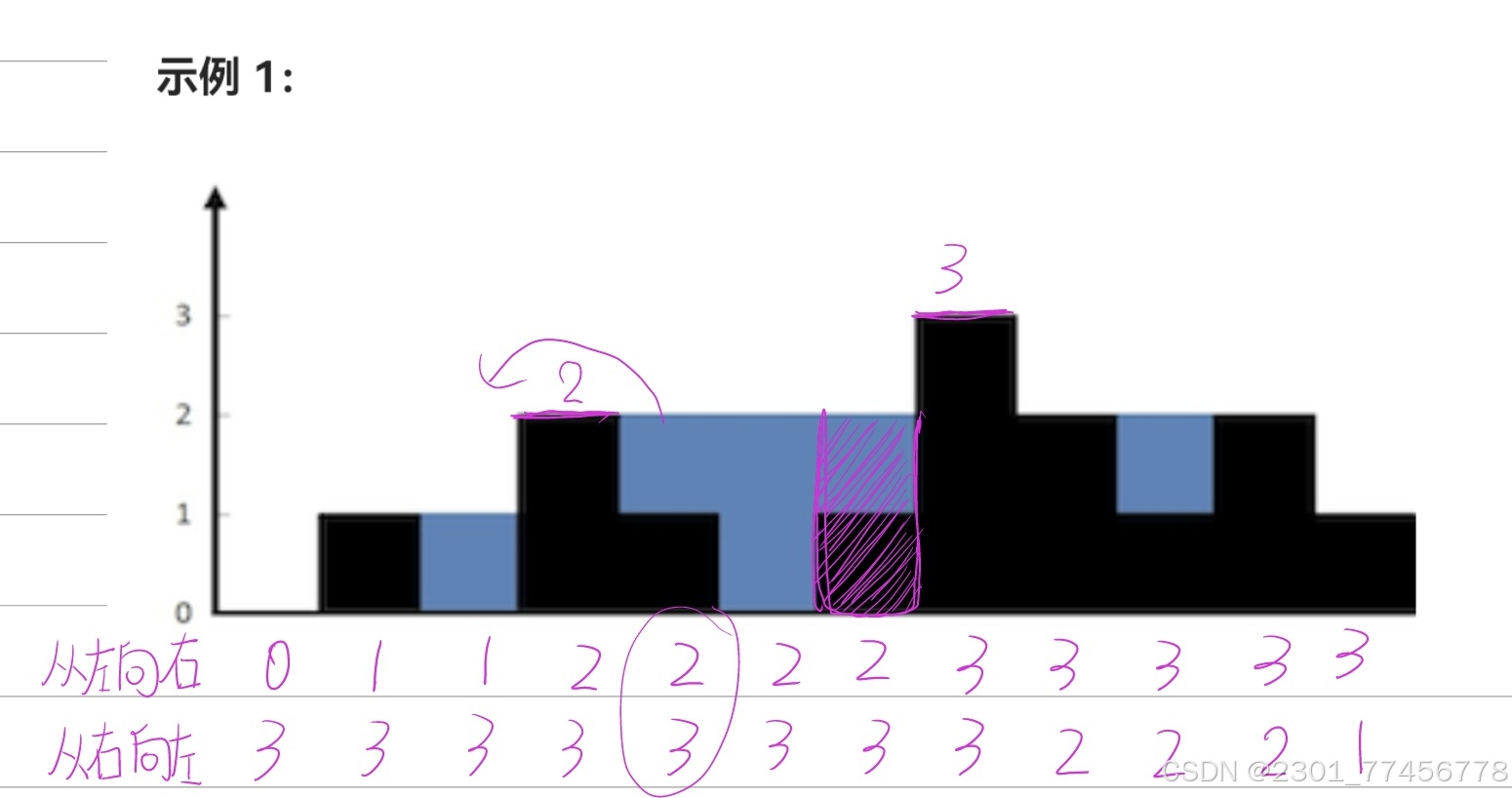
       下一步，对每个宽度为1的小木桶，取对应的left数组和right数组中小的那个，再减去本身的宽度，就是可以接水的面积，最后累加即可。整体代码如下：

class Solution {
public:
    int trap(vector<int>& height) {
        int n=height.size();
        int sum=0;
        //分别设置从左向右和从右向左两个数组
         vector<int> left(n); 
         vector<int> right(n);

        //计算从左往右的最大前缀
        left[0]=height[0];right[n-1]=height[n-1];
        for(int i=1;i<n;i++)
        {left[i]=max(left[i-1],height[i]);}

        //计算从右往左的最大前缀
        for(int i=n-2;i>=0;i--)
        {right[i]=max(right[i+1],height[i]);}

        //每个宽度想象成一个桶，哪个短用哪个，再累加算面积
        for(int i=0;i<n;i++)
        {sum+=min(left[i],right[i])-height[i];}
        return sum;
    }
};

方法二：相向双指针

      如下图所示，假设我让两个指针left和right移动到图示处，我只算出前面一部分前缀和后面一部分后缀，相当于把所有前面的A区看成一个整体，已经得到一个最大前缀是1，把所有后面的C区全看成一个整体，得到最大后缀是3。这时候，我要是想判断B区里面m和n两个木桶的雨水，对于m木桶来说，更新后最短的板反正已经确定了肯定是左边这个1，所以直接就能知道m桶的雨水应该是当前最大前缀1减去本身0就是1，说明m桶能接的水是1。反观n这个木桶，只可以确定紧挨着它的右边最长的板是3，无法判断左边的板有没有更短的。

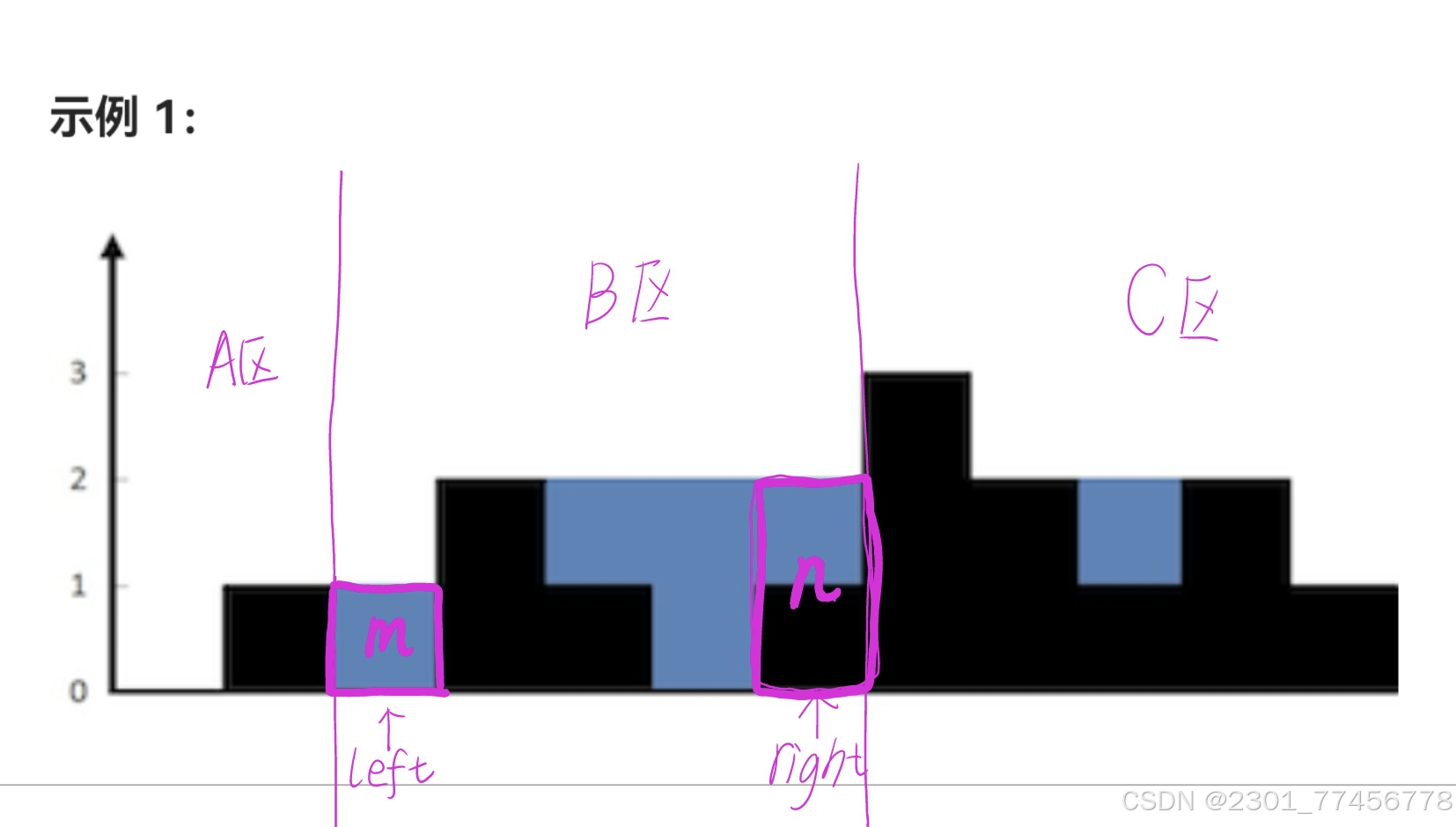
       所以，可以设置相向双指针，从两边开始向中间移动，如果左边最长前缀小于右边最长前缀，说明左边这个数值有用，也就是m桶可以算进来，反之，就是右边这个数值有用。这个思路的精妙之处在于一边遍历一边更新，每次while循环都比较左右前缀的值，哪边小哪边的桶就有用，就可以累计进入雨水。完整代码如下：

class Solution {
public:
    int trap(vector<int>& height) {
        int n=height.size();
        int sum=0;
        int left=0,right=n-1;
        //记录左右前缀最大值，一边遍历一遍更新
        int pre_max=0,suf_max=0;
        while(left<right)
        {
            //while里面每一个时刻都比较左右前缀的最大值，里面小的那个有用，把小的那个更新移动
            pre_max=max(pre_max,height[left]);
            suf_max=max(suf_max,height[right]);
            if(pre_max<suf_max)
            {
                sum+=pre_max-height[left];
                left++;
            }
            else
            {
                sum+=suf_max-height[right];
                right--;
            }
        }
        return sum;
    }
};

       好啦，今天的学习就到这里，如果有什么问题欢迎各位小伙伴在评论区和我交流哦~