AK F.*ing leetcode 流浪计划之费马小定理与组合数取模

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

费马小定理与证明

参考 https://zhuanlan.zhihu.com/p/594859227

费马小定理：如果p是一个质数，而正整数a不是p的倍数，那么a^(p-1)≡1（mod p）。

证明：

引理1 S={1a, 2a, 3a, …, (p-1)a}，S里所有数都不是p的倍数

由于 1到p-1都小于p, a也不能被p整除，说明a, 1到p-1 这些数都没有因子p。

由此引理1得证明。

引理2 S中所有元素对p取模不为0，且正好为集合 N = {1,2,3,…, p-1}

由引理1可知，对于任意小于p的两个不相同整数, i, j, ia%p != ja%p !=0。

假设 ia%p = ja%p，则 i%p * a%p = j%p * a%p, 得出i=j，与条件矛盾。

所以，对于S%p所有数字不相同，总个数为p-1个，由鸽巢原理可知，引理2正确。

根据引理2，可得到 $\prod _S\%p=\prod _N\%p$

两边整理得到 $a^{p-1}(p-1)!\%p=(p-1)!\%p$

由于gcd(p, (p-1)!)=1, 得到 a^(p-1)%p=1。

逆元

定义

已知整数a,p , a与p互质，如果存在一个数c<p使得 a*c%p=1, 则称c为a在模p下的逆元，记c=a^-1 %p;
通俗理解就是求(1/a)%p。

用费马小定理求逆元

a^(p-1)≡1（mod p）

可知 a*a^(p-2)%p=1

从定义可知 a在模p下的逆元为 a^(p-2)%p, 一般p是比较大的质数，可以使用快速幂求解。

typedef long long lld;
 
lld MOD = 998244353;
 
const int N = 1e6 + 10;
 // a的逆元为 fastmi(a, p-2)
lld fastmi(lld a, lld n) {
   
   
	lld ans = 1;
 
	while (n) {
   
   
		if (n & 1)ans = ans*a%MOD;
		
		a *= a;
		a %= MOD;
		n >>= 1;
	}
 
	return ans;
}

组合数取模

已经知p是一个比较大的质数（超过10的7次），求组合数C(n, m) , 0<=m<=n。

打表法

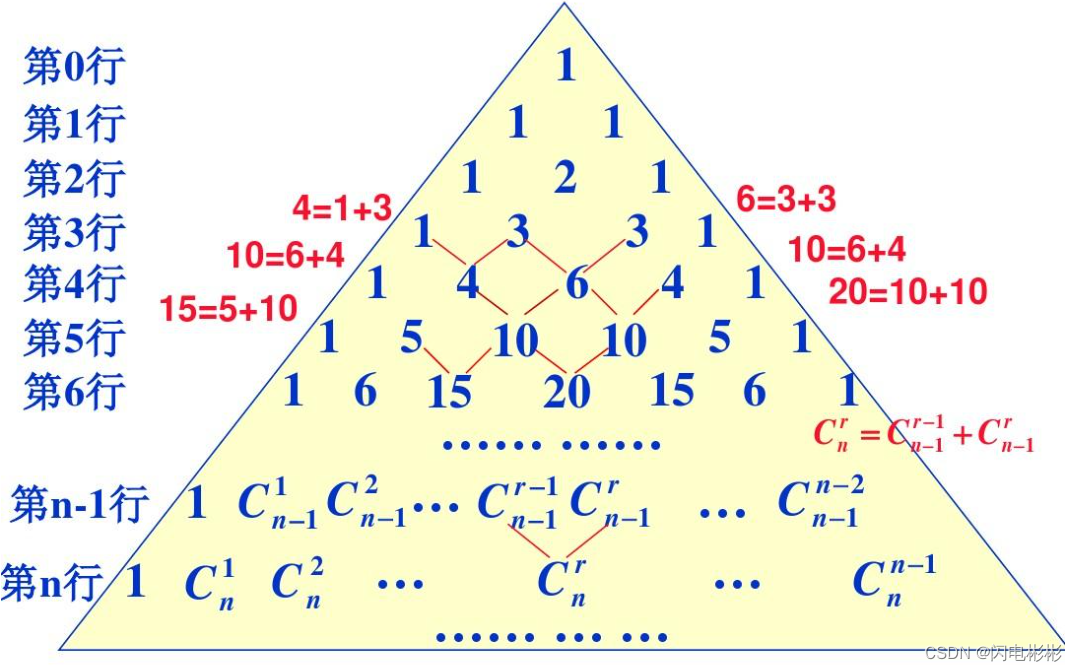
当n<=1000时，可以使用扬辉三角打表法。
用一个下三角矩阵存储组合数结果。
利用公式C[i][j] =( C[i - 1][j-1] + C[i - 1][j])%p，求解;

lld C[1010][1010];
 
void initC() {
   
   
	C[0][0] = 1;
	C[1][0] = C[1][1] = 1;
 
	for (int i = 2; i < 1010; i++) {
   
   
		C[i][0] = C[i][i] = 1;
		for (int j = 1; j < i; ++j) C[i][j] =( C[i - 1][j-1] + C[i - 1][j])%MOD;
	}
}

逆元法

$C_n^m=\frac{A_n^m}{m!}$