切比雪夫（最小区域法）圆拟合算法

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

本期话题：切比雪夫（最小区域法）圆拟合算法

相关背景和理论
点击前往
主要介绍了应用背景和如何转化成线性规划问题

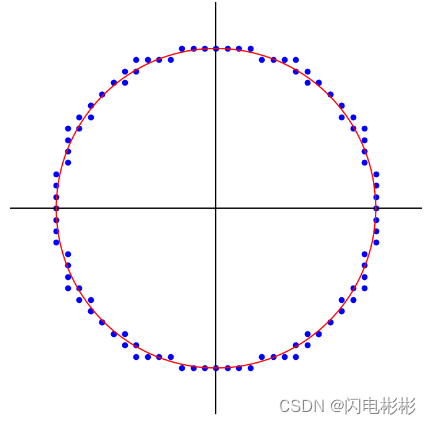
圆拟合输入和输出要求

输入

1. 10到631个点，全部采样自2D圆附近。
2. 每个点3个坐标，坐标精确到小数点后面20位，最后1个坐标为0。
3. 坐标单位是mm, 范围[-500mm, 500mm]。

输出

1. 圆心1点C，用三个坐标表示。
2. 半径r。
3. 圆度F，所有点到圆距离最大的2倍。

F的最小区域法理解

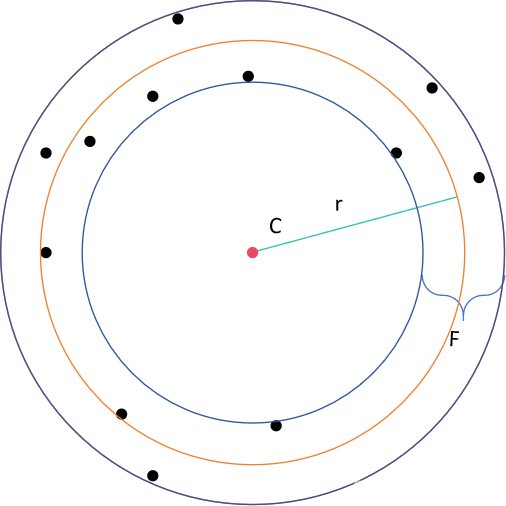
黑色为点云。

对于圆来讲，最小区域是指用两个同心圆夹住点云，使得圆之间的半径之差最小。这个最小值就是F。拟合结果就是两圆中间的圆（橙色圆）。

精度要求

1. C点到标准圆心距离不能超过0.0001mm。
2. r与标准半径的差不能超过0.0001mm。
3. F与标准圆度误差不能超过0.00001mm。

圆优化标函数

根据认证要求，圆拟合转化成数学表示如下：

圆参数化表示

1. 圆心C = (x0, y0,0)。
2. 半径r。

$圆方程(x-x_0{)}^2+(y-y_0{)}^2=r^2$

点到圆距离

第i个点 pi(xi, yi, 0)。

根据定义得到距离

$d_i=\Vert (p_i-X_0)\Vert -r$

展开一下：

$d_i=r_i-r$

$r_i=\sqrt{(x_i-x_0{)}^2+(y_i-y_0{)}^2}$

优化能量方程

能量方程 $H=f(X0,r)=\underset{1}{\overset{n}{\max }}|d_i|$

上式是一个4元二次函数中，X0, r是未知量，拟合2D圆的过程也可以理解为优化X0, r使得方程E最小。

可以对上述方程求导，使得导数等于0取得最值。但是求导后会变成一个比较复杂的方程组，不好解。可以使用高斯牛顿迭代法来求解。

转化为线性规划

$设a=(x_0,y_0,r),d_i=F(x_i;a),引入\Gamma ＝\stackrel{n}{\underset{i=1}{\mathrm{MAX}}}|d_i|$

根据上述定义，可以将原来的最值问题转化为下述条件

对于所有点应该满足

$F(x_i;a)\le$