最小二乘3D圆拟合(高斯牛顿法)

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

本期话题：最小二乘3D圆拟合

相关背景资料
点击前往

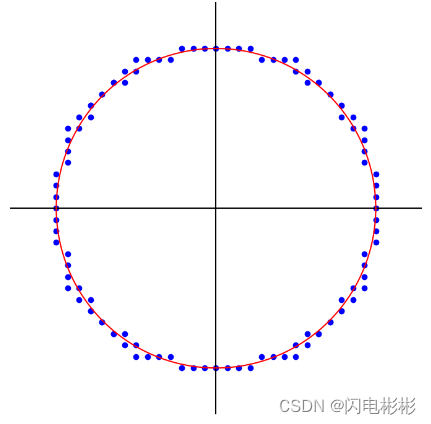
3D圆拟合输入和输出要求

输入

1. 8到50个点，全部采样自3D圆上。
2. 每个点3个坐标，坐标精确到小数点后面20位。
3. 坐标单位是mm, 范围[-500mm, 500mm]。

tips
输入虽然是严格来自3D圆，但是由于浮点表示，记录的值和真实值始终是有微小的误差，点云到拟合圆的距离不可能完全为0。

输出

1. 1点X0表示 圆心，用三个坐标表示。
2. 法向A代表圆所在平面法向。
3. 圆半径r。

精度要求

1. X0点到标准圆心距离不能超过0.0001mm。
2. 法向A与圆法向夹角不能超过0.0000001rad。
3. r与标准半径的差不能超过0.0001mm。

3D圆优化标函数

根据论文，圆拟合转化成数学表示如下：

圆参数化表示

1. 圆心为1点X0 = (x0, y0, z0)。
2. 法向A=(a,b,c)。
3. 半径r。

$圆方程\begin{array}{c}(x-x_0{)}^2+(y-y_0{)}^2+(z-z_0{)}^2=r^2\\ a(x-x_0)+b(y-y_0)+c(z-z_0)=0\end{array}$

能量方程

第i个点 pi(xi, yi, zi)。

定义距离如图

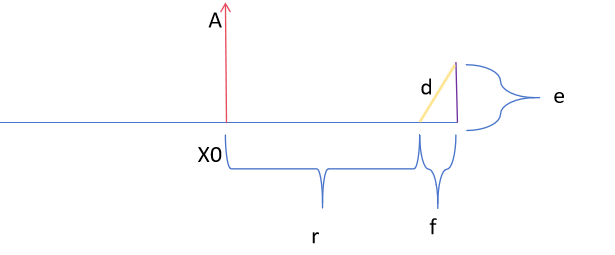
根据勾股定理，黄色线为距离。

$d_i=\sqrt{e_i^2+f_i^2}$

根据定义得到能量方程

$E=\sum _1^n{d}_i^2=\sum _1^n(e_i^2+f_i^2)$

$\begin{array}{l}{e}_i=a(x_i-x_0)+b(y_i-y_0)+c(z_i-z_0)\\ f_i=\sqrt{u_i^2+v_i^2+w_i^2}-r\end{array}$

$\begin{array}{l}{u}_i=c(y_i-y_0)-b(z_i-z_0)\\ v_i=a(z_i-z_0)-c(x_i-x_0)\\ w_i=b(x_i-x_0)-a(y_i-y_0)\end{array}$

最小二乘优化能量方程

能量方程 $E=f(X0,A,r)=\sum _1^n{d}_i^2$

上式是一个7元二次函数中，X0, A, r是未知量，拟合3D圆的过程也可以理解为优化X0, A, r使得方程E最小。

上述方程直接求导不好解，可以使用高斯牛顿迭代法。

高斯牛顿迭代法

用于解非线性最小二乘问题。同时，高斯牛顿法需要比较可靠的初值，所以寻找目标函数的初值也是一个比较关键的步骤。

基本原理

$设a=(a_0,a_1,...,a_n)是待求解向量，\hat{a}是初始给定值，a=\hat{a}+\Delta a,\Delta a是我们每次迭代后移动的量$

$定义距离函数为F(x,a),d_i=F(x_i,a),进行泰勒1阶展开，F(x,a)＝F(x,\hat{a})+\frac{\partial F}{\partial \hat{a}}\Delta a=F(x,\hat{a})+J\Delta a$

$每次迭代，其实就是希望通过调整\Delta a使得J\Delta a＝-F(x,\hat{a})$

$J=\left[\begin{array}{cccc}\frac{\partial F(x_0,a)}{\partial a_0}& \frac{\partial F(x_0,a)}{\partial a_1}& ...& \frac{\partial F(x_0,a)}{\partial a_n}\\ & & & \\ \frac{\partial F(x_1,a)}{\partial a_0}& \frac{\partial F(x_1,a)}{\partial a_1}& ...& \frac{\partial F(x_1,a)}{\partial a_n}\\ & & & \\ ...& ...& ...& ...\\ & & & \\ \frac{\partial F(x_n,a)}{\partial a_0}& \frac{\partial F(x_n,a)}{\partial a_1}& ...& \frac{\partial F(x_n,a)}{\partial a_n}\end{array}\right]$