三角网格半边数据结构设计与实现

功能

• 读取obj三角网格文件，将数据转化成半边数据结构。
• 将半边数据结构写入obj文件。
• 给定一个三角面，找到3个点按逆时针排列。
• 给定1个点，找到与该点相邻的面。
• 给定1个点，找到从该点出发的边。
• 给定1个点，找到进入到该点的边。
• 给定1个点，找到与该点相邻的点。
• 给定1条边，找到与该边相邻的面。
• 给定1个面及其1边，找到与该边相邻的另一面（如果有）。
• 判断点是否在边界点。
• 判断边是否为边界。

数据结构设计及功能算法

半边数据结构中的一条边分成2个方向，分别属于被边分割的2个部分。
每条边都有自己的后继和前驱，从一条边开始遍历后继，最后可以形成一个环。

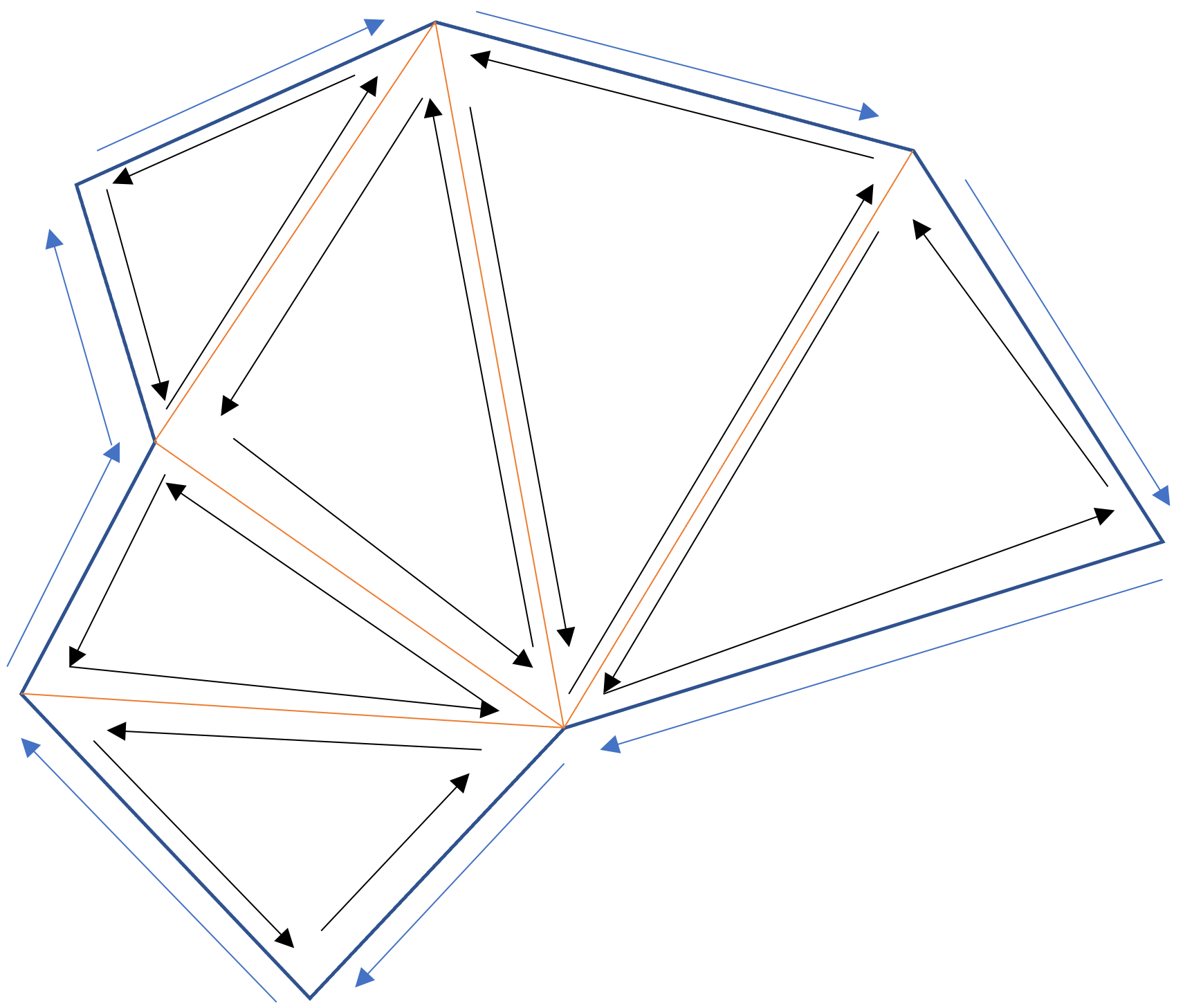
上图中箭头指向的边就是下一条边，反之是上一条边。
每个三角形内部会形成循环，最外部的边界所有边也会形成循环。如果内部有循环说明有空洞。

数据结构定义

// 点定义
class MVert
{
   
   
private:
	int index_;// 编号， 从0开始

	MPoint3 point_; // 坐标

	MHalfedge* he_; // 从该点出发的一条半边，尽量设置成边界边（如果有）
};

// 半边结构
class MHalfedge {
   
   
private:
	int index_; // 编号

	MVert* v_; // 半边起点
	MEdge* e_; // 半边对应的全边
	MPolyFace* poly_face_; // 半边对应的三角面

	MHalfedge* next_, * prev_; // 后继和前驱

	MHalfedge* pair_; // 对应的另一条半边
};

// 全边结构
class MEdge {
   
   
private:
	int index_; // 编号

	MVert* v1_; MVert* v2_; // 对应2点

	MHalfedge* he_; // 其中一条半边
};

// 三角面定义
class MPolyFace
{
   
   
private:
	int index_; // 编号

	MHalfedge* he_begin_; // 开始半边
};

// 物体实体定义

class PolyMesh {
   
   
private:

    std::vector<MHalfedge *> half_edges_;
    std::vector<MVert *> vertices_;
    std::vector<MEdge *> edges_;
    std::vector<MPolyFace *> polygons_;
    
};

算法过程

• 读取obj三角网格文件，将数据转化成半边数据结构。

1. 读入点入到数组里。
2. 对于每个面，读入面的三个点。
3. 构建出三条边，如果已经构建则复用。
4. 三条边初始后继和前驱都是自己。
5. 建立边与面的关系。
6. 调整边的前驱和后继关系。返回步骤2.
   上述过程比较复杂的是调整边的前驱和后继关系。下面以图示说明。每次调整的是三角形2条相邻边的关系。
   

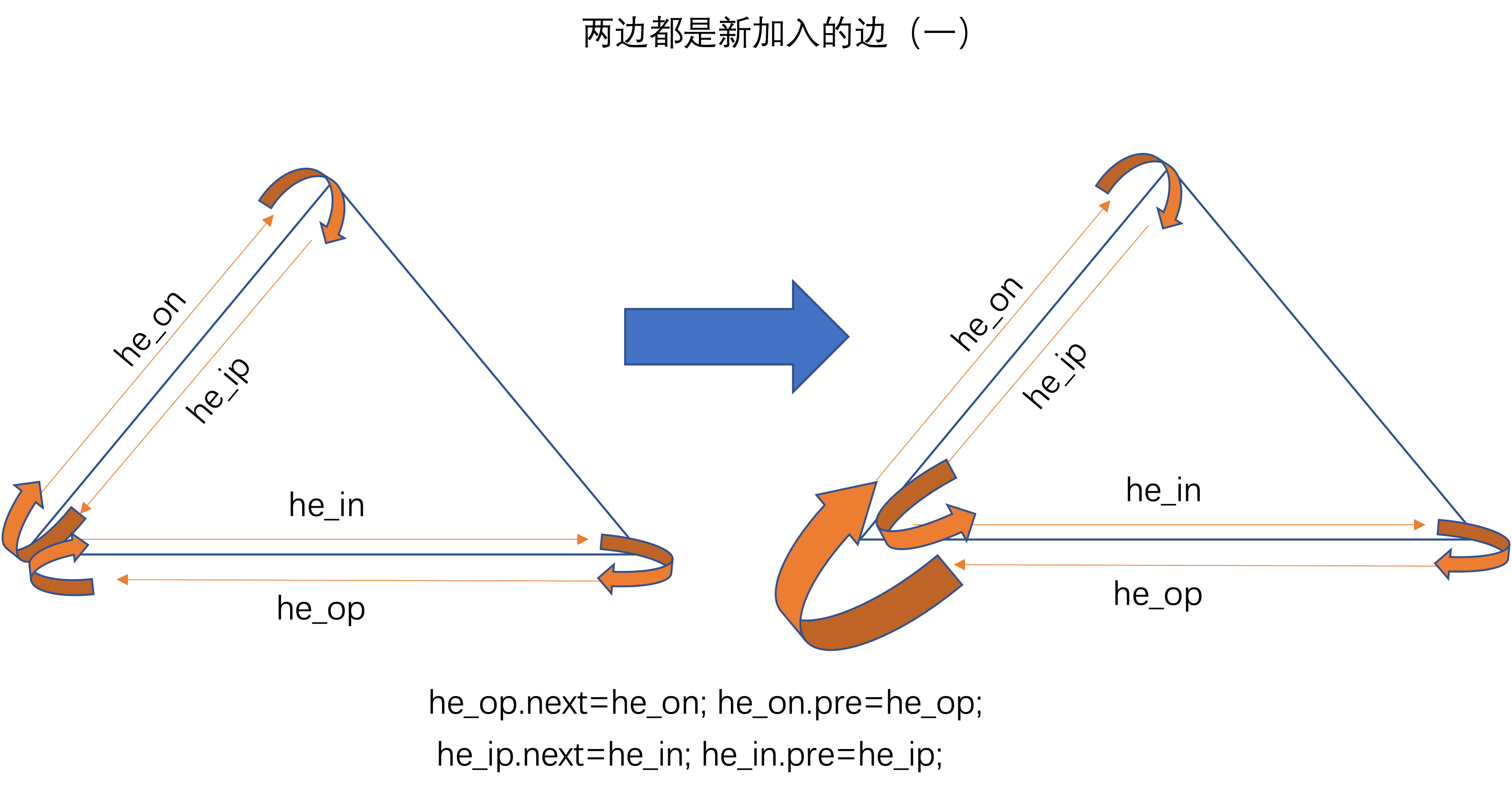
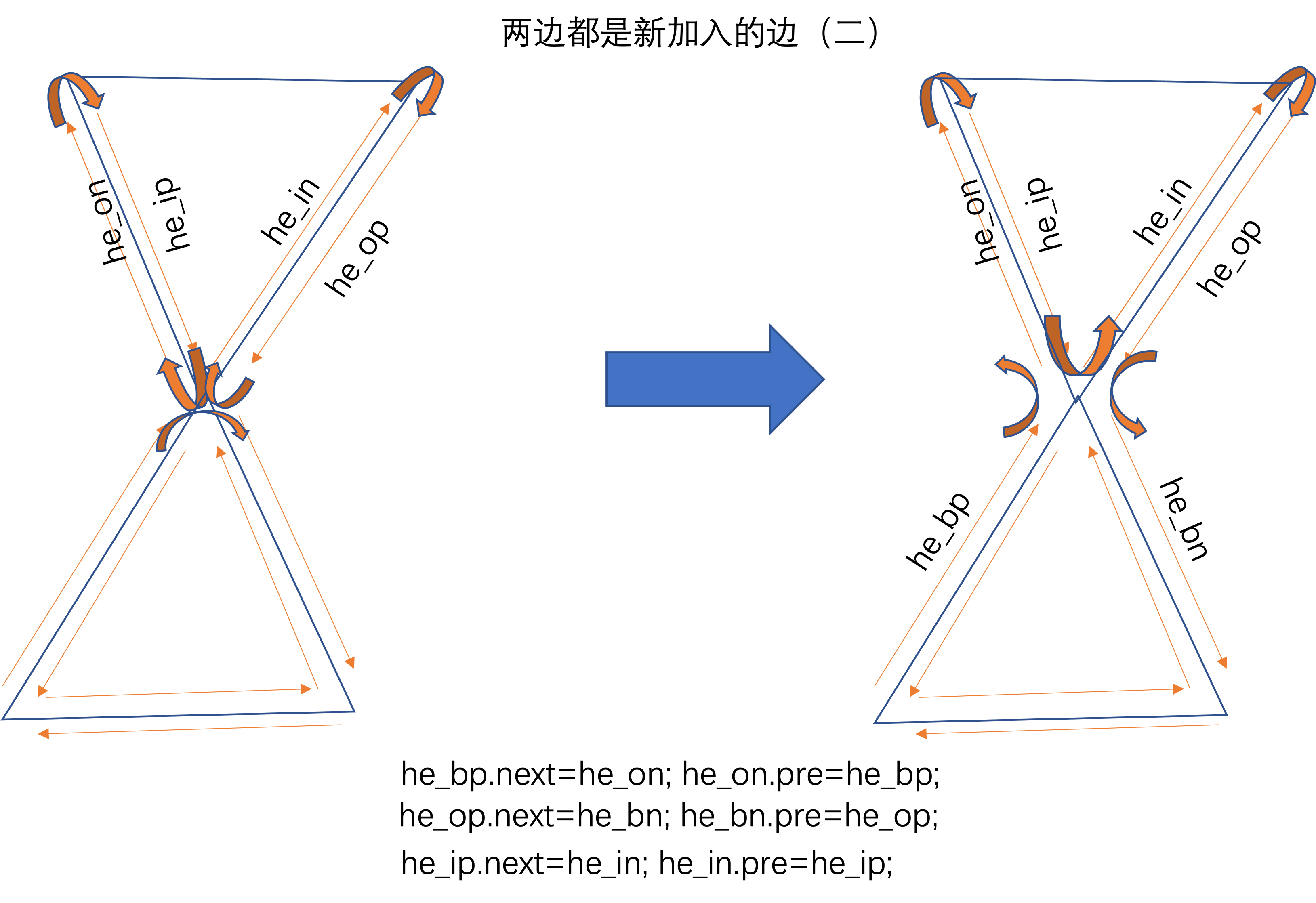
上图中he_bp = he_bn.pre

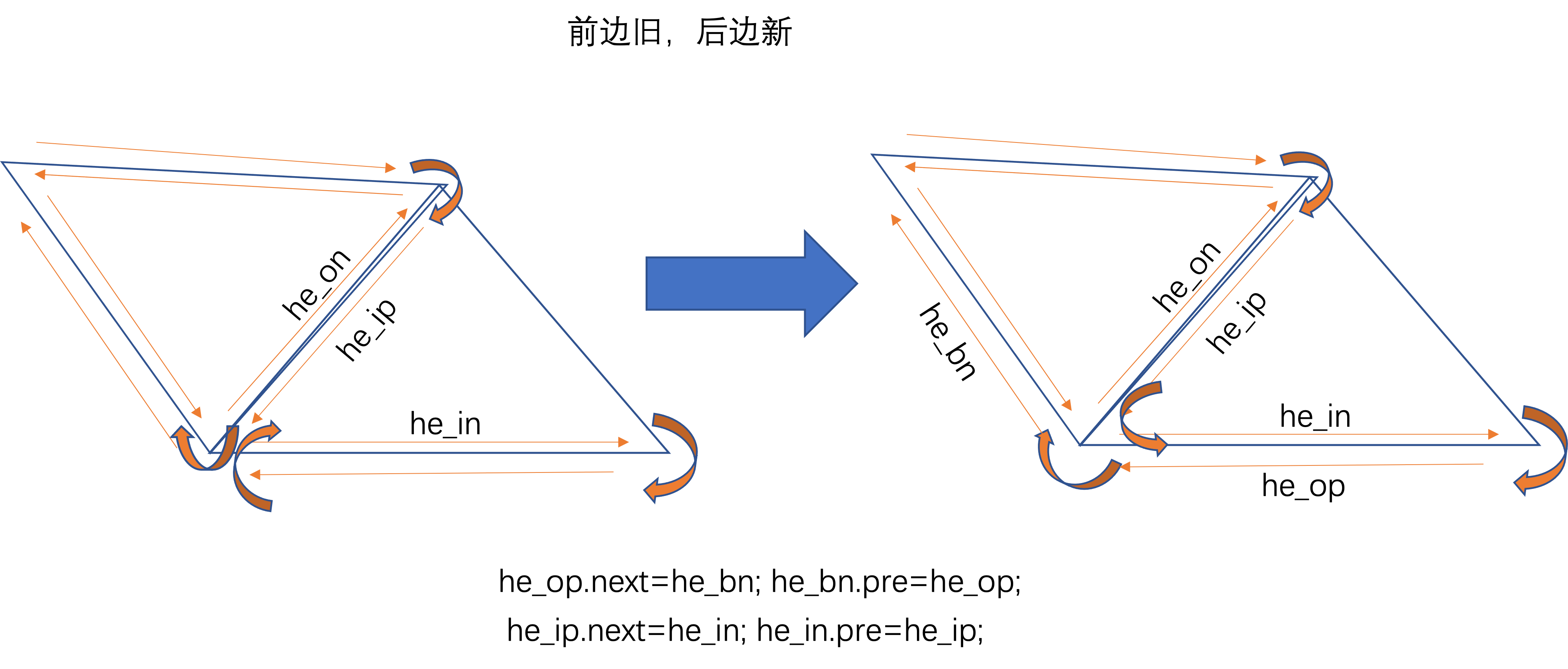
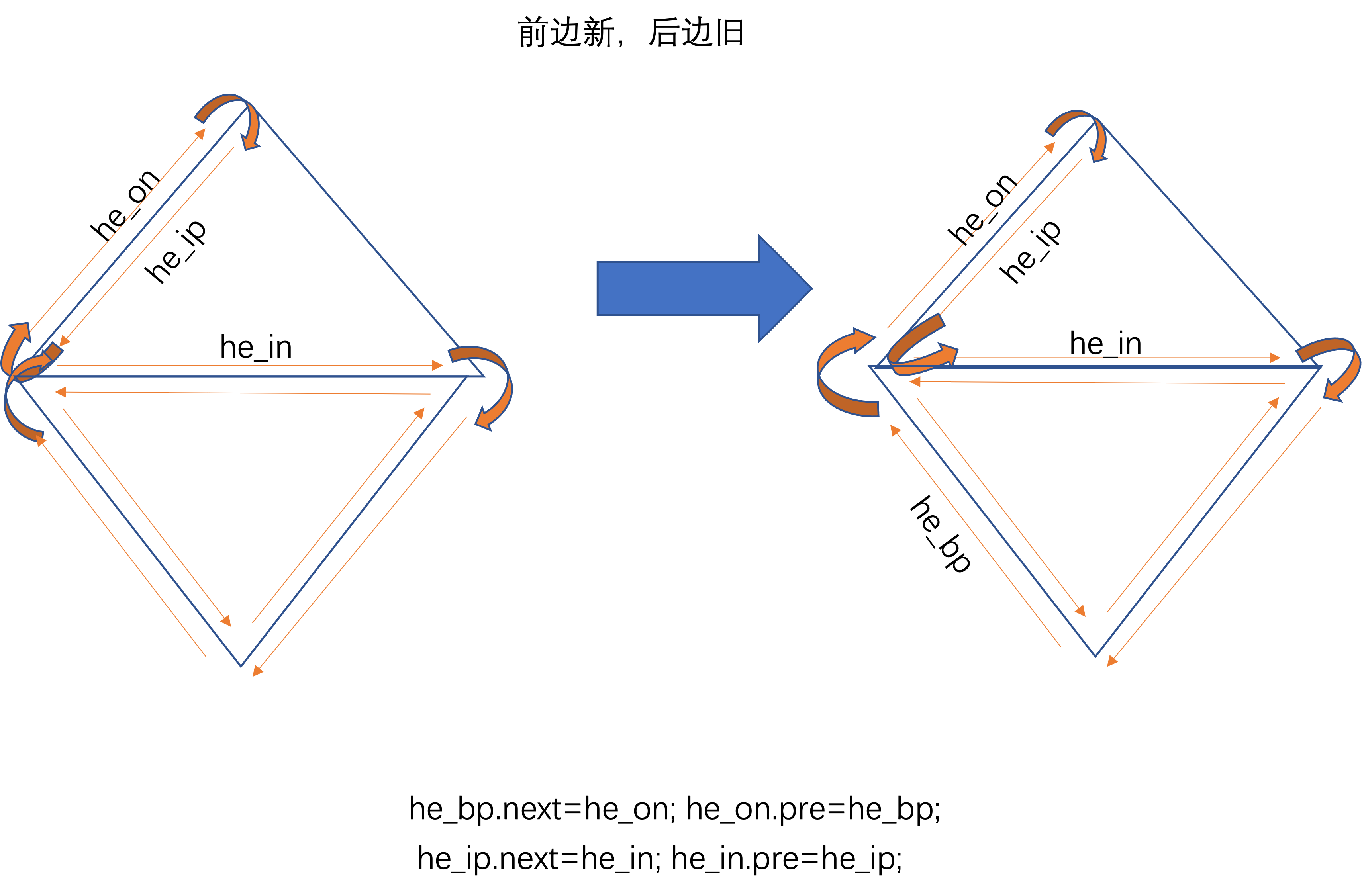
上图中he_bp=he_in.pre

• 将半边数据结构写入obj文件。

1. 遍历点，写入obj文件。
2. 遍历面，按照逆时针写入三点的编号。

• 给定一个三角面，找到3个点按逆时针排列。
  找到三角面的第一条边he，拿到边的出发点，再找he.next，直到回到第一条边，找到3点。

• 给定1个点，找到与该点相邻的面。
  
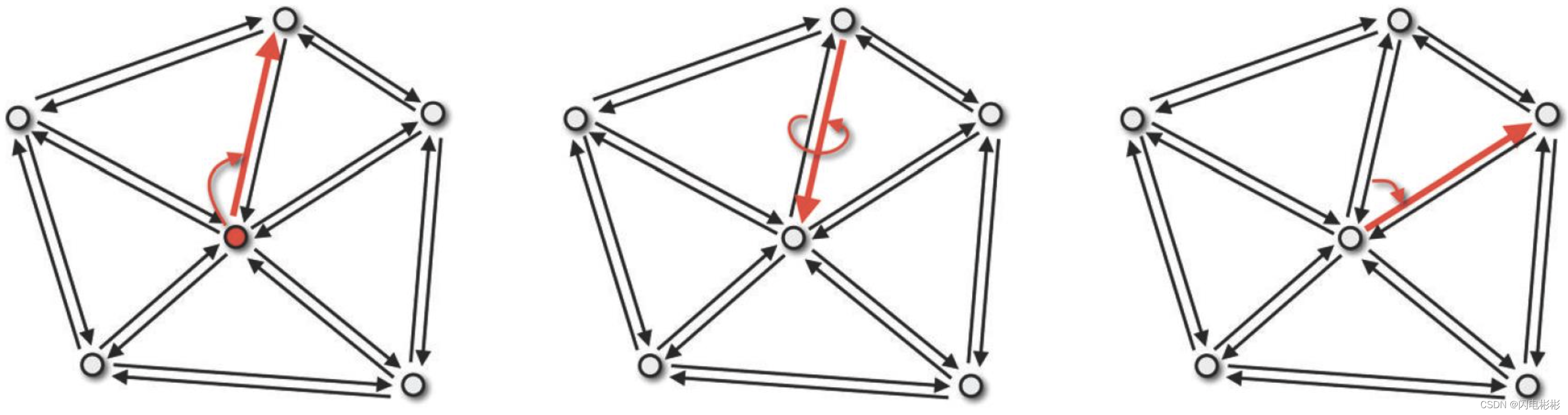
  先找到点的第一条边he， he.pair.next就是从点出发的下一条，如此反复找到所有边，就可以找到所有面。

• 给定1个点，找到从该点出发的边。
  同上。

• 给定1个点，找到进入到该点的边。
  同上，先找到第1条边he = v.he.pair, 下一条边是he.next.pair，如此反复找到所有边。

• 给定1个点，找到与该点相邻的点。
  同上，找到所进入的边，边的起点就是相邻点。

• 给定1条边，找到与该边相邻的面。
  找出2条半边he, he.pair， 半边邻接的面就是与该边相邻的面。

• 给定1个面及其1边，找到与该边相邻的另一面（如果有）。
  找出边的2个半边，判断哪边与现有面连接，另一条相邻的面就是所求的面。

• 判断点是否在边界点。
  扫描从该点出发的所有边，判断是否存在一条边没有面连接。

• 判断边是否为边界。
  是否有邻接面。

代码实现

https://github.com/LightningBilly/ACMAlgorithms/tree/master/图形学算法/半边数据结构/glTriangle/

//
// Created by chenbinbin on 2022/3/30.
//
#include "MPoint3.h"
#include "MVector3.h"
#ifndef GLTRIANGLE_POLYMESH_H
#define GLTRIANGLE_POLYMESH_H

class MVert;
class MEdge;
class MHalfedge;
class MPolyFace;

// 点定义
class MVert
{
   
   
private:
    int index_;// 编号， 从0开始

    MPoint3 point_; // 坐标

    MHalfedge* he_; // 从该点出发的一条半边，尽量设置成边界边（如果有）
public:
    MVert() : index_(-1), point_(0, 0, 0), he_(nullptr){
   
   }
    MVert(double x, double y, double z) : index_(-1), point_(x, y, z), he_(nullptr) {
   
   }
    ~MVert() {
   
    index_ = -1; }

public:
    MHalfedge* const halfEdge() {
   
    return he_; }
    const MHalfedge* const halfEdge() const {
   
    return he_; }

    void setHalfedge(MHalfedge* he) {
   
    he_ = he; }

    void setPosition(MPoint3 new_point) {
   
    point_ = new_point; }
    void setPosition(double x, double y, double z) {
   
    point_ = MPoint3(x, y, z); }
    MPoint3 position()