Nearest Common Ancestors

最新推荐文章于 2023-06-02 21:01:49 发布

chen_zan_yu_

最新推荐文章于 2023-06-02 21:01:49 发布

阅读量172

点赞数

CC 4.0 BY-SA版权

分类专栏： VJ 最短路

本文链接：https://blog.youkuaiyun.com/chen_zan_yu_/article/details/98481480

VJ 同时被 2 个专栏收录

105 篇文章

订阅专栏

最短路

16 篇文章

订阅专栏

本文深入讲解LCA（最近公共祖先）算法，通过实例解析Tarjan思想在深搜树中的应用，展示如何通过并查集优化算法，降低时间复杂度至O(n+q)，适用于有根树结构的数据查询。

Nearest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 38307		Accepted: 19085

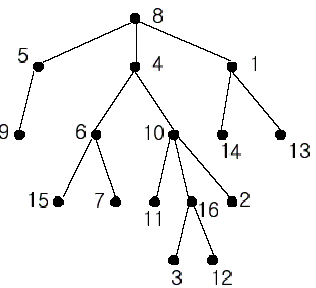
Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:

In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.

Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

Sample Output

4
3

Source

Taejon 2002

这是我的第一篇LCA文章，可以看看这篇关于LCA算法简介

LCA 最近公共祖先

这篇博客写的非常不错，我就是看这个学会的。

第一次写最近公共祖先问题，用的邻接表指针。

对于一棵有根树，就会有父亲结点，祖先结点，当然最近公共祖先就是这两个点所有的祖先结点中深度最大的一个结点。

/ \

2 3

比如说在这里，如果0为根的话，那么1是2和3的父亲结点，0是1的父亲结点，0和1都是2和3的公共祖先结点，但是1才是最近的公共祖先结点，或者说1是2和3的所有祖先结点中距离根结点最远的祖先结点。

在求解最近公共祖先为问题上，用到的是Tarjan的思想，从根结点开始形成一棵深搜树，非常好的处理技巧就是在回溯到结点u的时候，u的子树已经遍历，这时候才把u结点放入合并集合中，这样u结点和所有u的子树中的结点的最近公共祖先就是u了，u和还未遍历的所有u的兄弟结点及子树中的最近公共祖先就是u的父亲结点。以此类推。。这样我们在对树深度遍历的时候就很自然的将树中的结点分成若干的集合，两个集合中的所属不同集合的任意一对顶点的公共祖先都是相同的，也就是说这两个集合的最近公共最先只有一个。对于每个集合而言可以用并查集来优化，时间复杂度就大大降低了，为O(n + q)，n为总结点数，q为询问结点对数。

另外Tarjan解法，是一个离线算法，就是说它必须将所有询问先记录下来，再一次性的求出每个点对的最近公共祖先，只有这样才可以达到降低时间复杂度。另外还有一个在线算法，有待学习

#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
const int N=100005;
int n;
vector<int> vec[N];
int pre[N];
bool vis[N];
bool root[N];
int u,v;
int Find(int x)
{
    return x==pre[x]?x:Find(pre[x]);
}
void mix(int x,int y)
{
    int xx=Find(x);
    int yy=Find(y);
    if(xx!=yy)
    {
        pre[yy]=xx;//不可搞错顺序，xx是yy的祖先
    }
}
void Init()
{
    for(int i=0; i<=n; i++)
    {
        vec[i].clear();
        pre[i]=i;
        root[i]=true;
        vis[i]=false;
    }
}
void Tarjan(int x)
{
    for(int i=0; i<(int)vec[x].size(); i++)
    {
        Tarjan(vec[x][i]);
        mix(x,vec[x][i]);
    }
    vis[x]=true;
    if(u==x&&vis[v]==true)
    {
        printf("%d\n",Find(v));
        return ;
    }
    if(v==x&&vis[u]==true)
    {
        printf("%d\n",Find(u));
        return ;
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        Init();
        for(int i=0; i<n-1; i++)
        {
            int a,b;
            scanf("%d%d",&a,&b);
            vec[a].push_back(b);
            root[b]=false;
        }
        scanf("%d%d",&u,&v);
        for(int i=1; i<=n; i++)
        {
            if(root[i]==true)
            {
                Tarjan(i);
                break;
            }
        }
    }
    return 0;
}