混流生产在数字化工厂投产序列平衡与仿真中的应用研究【附数据】

✅ 博主简介：擅长数据搜集与处理、建模仿真、程序设计、仿真代码、论文写作与指导，毕业论文、期刊论文经验交流。

 ✅ 具体问题可以私信或扫描文章底部二维码。

---

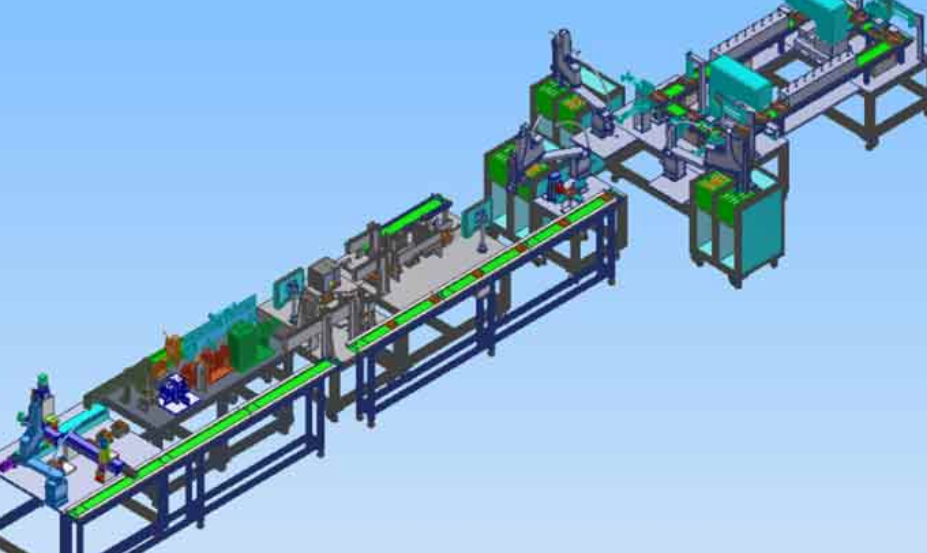
（1）铝合金门窗混流生产线的数字化工厂仿真框架

在智能制造的背景下，铝合金门窗混流生产线面临着提高生产效率和满足个性化需求的双重挑战。数字化工厂仿真技术的应用，为解决这些问题提供了新的途径。本文首先概述了铝合金门窗生产的数字化工厂内涵及关键技术，包括生产单元、物流系统、信息系统等，并提出了一个独具特色的仿真框架。该框架旨在通过仿真技术，实现生产过程的可视化、可监控、可优化和可管理，从而提高混流生产线的综合性能达到提升[124^]。

（2）生产线平衡优化和混流投产序列优化

生产线平衡优化是提高铝合金门窗混流生产线效率的关键。本文通过数字化工厂仿真技术，对车间的生产线进行建模和仿真，重点研究了生产线平衡优化和混流投产序列优化。通过仿真实验，开展了生产线平衡分析、作业模式对比分析、瓶颈分析与改善及物流运送系统优化等工作。这些优化措施综合改善了生产线的性能，提高了生产效率和流程时间，同时也提升了质量稳定性[128^]。

（3）仿真模型的建立与优化效果

采用em-plant软件建立了铝合金门窗混流生产系统仿真模型，并详细描述了建模的过程。在仿真模型验证后，通过设计仿真实验，对生产线进行了一系列的优化工作。确定了混流生产线的投产序列问题及优化目标，在em-plant中导入GA工具，设置遗传算法，求出基于总完工时间、各工位的平均空闲时间率及在制品数量最大值三目标下的最优解。这些优化工作对生产系统的性能提升具有良好的效果，提高了生产线的平衡率，减少了工作站闲置时间，并优化了节拍时间[130^]。

 

import numpy as np
import random

# 定义遗传算法的参数
POP_SIZE = 50  # 种群大小
GENE_LENGTH = 20  # 基因长度
MUTATION_RATE = 0.01  # 变异率
CROSSOVER_RATE = 0.8  # 交叉率
MAX_GENERATIONS = 100  # 最大迭代次数

# 初始化种群
def initialize_population(pop_size, gene_length):
    return [[random.randint(0, 1) for _ in range(gene_length)] for _ in range(pop_size)]

# 计算种群的适应度
def calculate_fitness(population):
    fitness = []
    for individual in population:
        # 假设适应度函数是简单的基因和
        fitness.append(sum(individual))
    return fitness

# 选择操作
def selection(population, fitness):
    weighted_fitness = [f / sum(fitness) for f in fitness]
    selected_idx = np.random.choice(range(POP_SIZE), size=POP_SIZE, replace=True, p=weighted_fitness)
    return [population[i] for i in selected_idx]

# 交叉操作
def crossover(parent1, parent2):
    if random.random() < CROSSOVER_RATE:
        crossover_point = random.randint(1, GENE_LENGTH - 1)
        child1 = parent1[:crossover_point] + parent2[crossover_point:]
        child2 = parent2[:crossover_point] + parent1[crossover_point:]
        return child1, child2
    else:
        return parent1, parent2

# 变异操作
def mutation(individual):
    for i in range(GENE_LENGTH):
        if random.random() < MUTATION_RATE:
            individual[i] = 1 - individual[i]

# 遗传算法主函数
def genetic_algorithm():
    population = initialize_population(POP_SIZE, GENE_LENGTH)
    
    for generation in range(MAX_GENERATIONS):
        fitness = calculate_fitness(population)
        selected_population = selection(population, fitness)
        
        new_population = []
        for i in range(0, POP_SIZE, 2):
            parent1, parent2 = selected_population[i], selected_population[i+1]
            child1, child2 = crossover(parent1, parent2)
            mutation(child1)
            mutation(child2)
            new_population.extend([child1, child2])
        
        population = new_population
        
        # 打印当前代的最佳适应度
        max_fitness_idx = np.argmax(fitness)
        print(f"Generation {generation}, Max Fitness: {fitness[max_fitness_idx]}")
    
    return population

# 运行遗传算法
best_solution = genetic_algorithm()