快速了解PCA

主成分分析 (PCA) ：

是用于降维的黄金标准。 5 分钟内，介绍完他：

1. 什么是PCA？

PCA是一种用于数据分析的统计技术，主要用于降维。在处理具有许多变量的大型数据集时，它非常有用，并且有助于简化数据的复杂性，同时保留尽可能多的变量和信息。

2. PCA如何工作

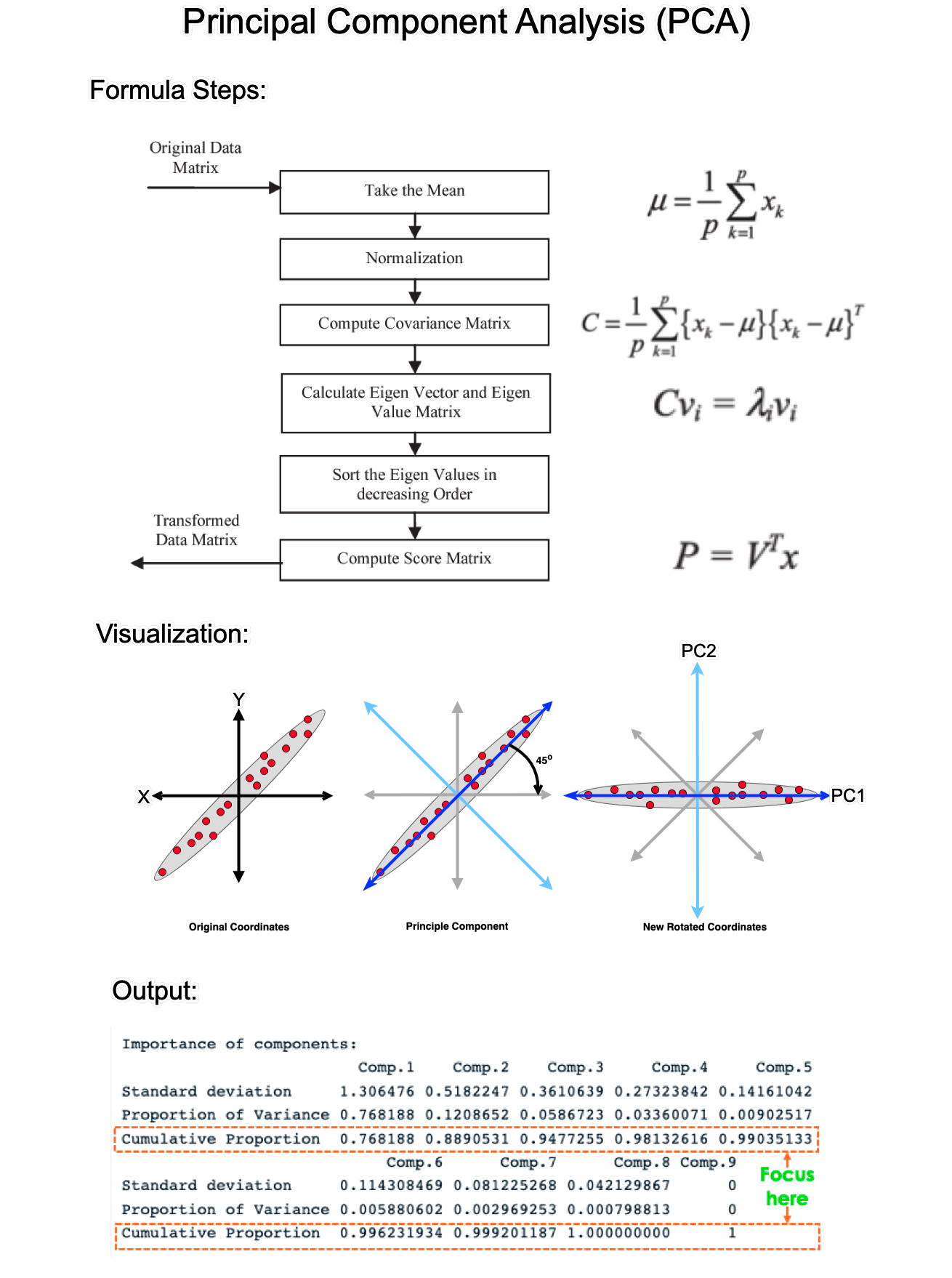
PCA有5个步骤；标准化、协方差矩阵计算、特征向量计算、选择主成分和转换数据。

3.标准化

PCA的第一步是对数据进行标准化。由于数据规模影响 PCA，因此对数据进行标准化（均值为 0，方差为 1）可确保分析不会偏向幅度较大的变量。

4.协方差矩阵计算

PCA着眼于数据的方差和协方差。方差是对单个特征的变异性的度量，而协方差是对两个特征一起变化的程度的度量。协方差矩阵是一个表，其中每个元素代表两个特征之间的协方差。

5.特征值和特征向量计算

根据协方差矩阵，计算特征值和特征向量。特征向量是方差最大的轴方向（即主成分），特征值是附加到特征向量的系数，给出每个主成分中携带的方差量。

6. 选择主成分

特征向量按其特征值降序排列。这按重要性顺序给出了组件。在这里，您可以决定保留多少个主成分。这通常基于累积解释方差比，即每个选定组件解释的方差量。

7. 变换数据

最后，将原始数据投影到主成分（特征向量）上，将数据变换到新的空间。这会产生一个新的数据集，其中变量不相关，并且前几个变量保留原始数据的大部分可变性。

8. 评估：

每个 PCA 分量都占数据集中总方差的一定量。解释的方差的累积比例只是每个变量的累积和

图文整理