leetcode72：编辑距离

最新推荐文章于 2024-06-25 14:15:48 发布

chandelierds

最新推荐文章于 2024-06-25 14:15:48 发布

阅读量224

点赞数

CC 4.0 BY-SA版权

分类专栏： Python 刷题 leetcode

本文链接：https://blog.youkuaiyun.com/chandelierds/article/details/90699033

leetcode 同时被 3 个专栏收录

123 篇文章

订阅专栏

刷题

98 篇文章

订阅专栏

Python

83 篇文章

订阅专栏

博客围绕某问题展开，解题思路采用动态规划，需建立dp表，多加一行一列，先单独考虑第一行和第一列。第一行对应插入操作，第一列对应删除操作，还提及根据dp表规律得出相关结论，最后给出代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：

在这里插入图片描述
思路：使用动态规划，建立dp表，注意此类问题都要多加一行和一列，并且第一行和第一列都要先单独考虑，如下图所示。
dp[i][j]表示word1的前i位转化到word2的前j位所需的最少步骤。

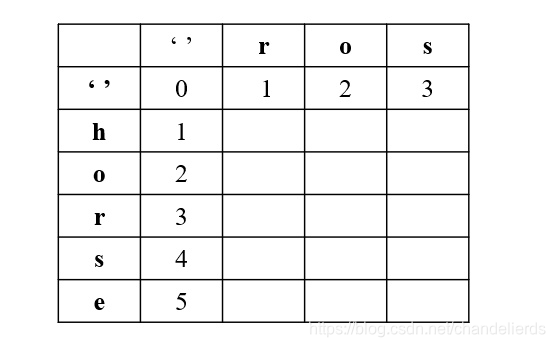
第一行，是word1为空，变成word2最少步数，就是插入操作
第一列，是word2为空，需要的最少步数，就是删除操作
根据所列dp表的规律，可以发现：
当word1[i] == word2[j],dp[i][j] = dp[i-1][j-1];
当word1[i] != word2[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1

代码实现

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        row = len(word1)
        col = len(word2)
        dp = [[0] * (col+1) for _ in range(row+1)]
#         print(dp)
        #第一列
        for i in range(1,row+1):
            dp[i][0] = dp[i-1][0] + 1
        #第一列
        for j in range(1,col+1):
            dp[0][j] = dp[0][j-1] + 1
        #注意dp标相应位置的的下标为两个字符下标+1
        for i in range(row):   
            for j in range(col):
                if word1[i] == word2[j]:
                    dp[i+1][j+1] = dp[i][j]
                else:
                    dp[i+1][j+1] = min(dp[i][j],dp[i+1][j],dp[i][j+1]) + 1
#         print(dp)
        return dp[-1][-1]