【论文笔记】RepVGG: Making VGG-style ConvNets Great Again

原创 已于 2023-07-07 20:35:46 修改 · 987 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#论文阅读 #深度学习 #cnn

于 2022-09-22 21:08:34 首次发布
RepVGG是一种在训练阶段采用多分支结构而在推理阶段转换为单一3x3卷积的网络，通过结构重参数化技术提高了网络的推理速度和内存效率。文章详细介绍了RepVGG的设计理念、工作原理及实验结果。

RepVGG: Making VGG-style ConvNets Great Again

目录

code

  • 提出了一种在训练阶段使用多分支网络结构，但是在inference时只有3x3卷积和Relu激活函数组成的单分支网络结构。
  • 网络主要用了一种结构重参数化方法a structural re-parameterization technique将训练时的多分枝融合为推理时的单分支结构。
  • 因为inference时网络很像VGG结构，和使用re-parameterization方法，所以命名为RepVGG.

1. Introduction

1.1 多分支网络结构的缺点

  1. 多分支的网络结构减少程序的并发性，在推理时的速度慢，降低内存利用率（比如ResNet中残差分支的add、Inception结构的concatenation操作）
  2. 一些组件比如说深度可分离卷积、channel shuffle（ShuffleNets）会增加内存消耗，并且适用性不好。

1.2 RepVGG优点

很多因素影响推理速度，FLOPs的数量值不能真实反应实际的速度。

  1. 网络推理时是一条单分支结构。

  2. 只使用3x3卷积核ReLU激活函数。证明了kernel=3的有效性
    在这里插入图片描述

  3. 网络简单，没有复杂的超参数。

  4. RepVGG是由RepVGGBlock堆叠的简单网络，能很好的达到速度和精度的折中。证明了该网络在分类和分割上的有效性。
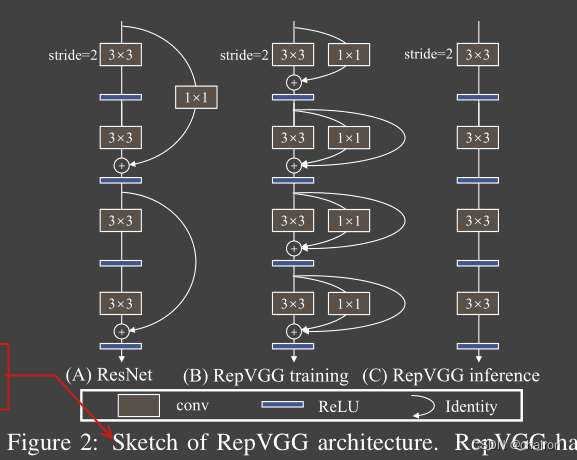
    在这里插入图片描述

2. Model Re-parameterization（模型重参数化）

2.1. DiracNet

通过对普通卷积进行编码得到的一条单分支网络，也是 一种 re-parameterization method。
W = d i a g ( a ) I + d i a g ( b ) W n o r m W = diag(a)I + diag(b){W_{norm}} W=diag(a)I+diag(b)Wnorm​
W W W是最终的卷积参数， a a a和 b b b是一个待学习的参数， W n o r m W_{norm} Wnorm​是归一化后的卷积核

另外，之前看过的ACBlock、DO-Conv 、ExpandNet也可以看作是一种模型重参数化方法，他们是把一个block看成一个卷积，去代替普通卷积，是一种component-level improvements 。而本文提出的方法对应一个扁平（plain)的卷积网络来说是很重要的。

2.2 Winograd Convolution

Winograd is a classic algorithm for accelerating 3 × 3 conv (only if the stride is 1).

3. Building RepVGG via Structural Re-param

3.1Simple is Fast, Memory-economical, Flexible

  • Fast：

    • == 内存访问成本(MAC)和并发度这两个影响推理速度的关键因素没有被考虑进FLOPs，因此FLOPs其实并不能反应真实的推理速度==
    • 此外，在分组卷积中，MAC占用了很大一部分时间。另一方面，在相同的FLOPs下，一个具有高并行度的模型可能比另一个具有低并行度的模型快得多。

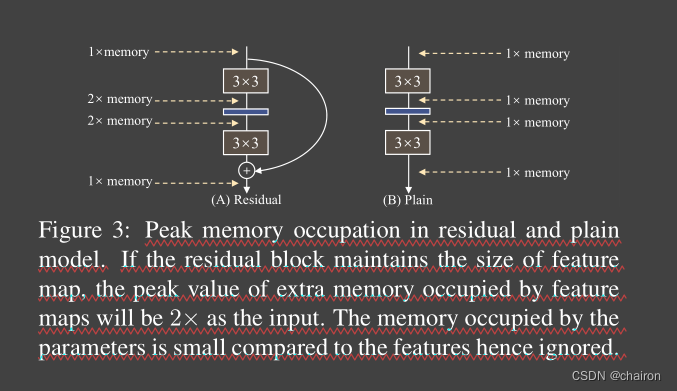
  • Memory-economical

    • 多分支网络结构内存使用是无效率的，因为在add或者concatenate操作之前，每个分支的结果都需要保持，因此会导致内存占用量的峰值变高。
    • 相比之下，普通单分支网络允许在操作完成时立即释放输入到特定图层的输入所占用的内存。在设计专门的硬件时，能做更深层次的内存优化，并降低内存单元的成本，这样我们就可以将更多的计算单元集成到芯片上。

  • Flexible

    • 比如残差连接，必须要相同size才能add，就需要做一些操作和限制
    • 多分枝结构限制了通道减枝（channel pruning）的运用
      在这里插入图片描述

3.2 对ResNet的一段精辟解释

ResNet，它构造了一个shortcut分支来将信息流建模为 y = x + f ( x ) y = x+ f (x) y=x+f(x)，并使用一个残差块来学习 f f f
当x和f (x)的维度不匹配时，它就变成了 y = g ( x ) + f ( x ) y = g (x) +f (x) y=g(x)+f(x)，其中 g ( x ) g (x) g(x)是一个由一个1×1conv实现的shortcut。对ResNets成功的一个解释是，这样的多分支体系结构使模型成为一个由许多较浅的模型[36]组成的隐式集成。

ResNet, which explicitly constructs a shortcut branch to model the information flow as y = x + f(x) and uses a residual block to learn f. When the dimensions of x and f(x) do not match, it becomes y = g(x)+f(x), where g(x)is a convolutional shortcut implemented by a 1×1 conv.

RepVGG使用了像是ResNet中的恒等连接的一个分支，并且加了一个1x1卷积分支，共三个卷积分支进行相加: y = x + g ( x ) + f ( x ) y =x+ g (x) +f (x) y=x+g(x)+f(x)

3.3 Re-param for Plain Inference-time Model

训练阶段：
M ( 2 ) = b n ( M ( 1 ) ∗ W ( 3 ) , µ ( 3 ) , σ ( 3 ) , γ ( 3 ) , β ( 3 ) ) + b n ( M ( 1 ) ∗ W ( 1 ) , µ ( 1 ) , σ ( 1 ) , γ ( 1 ) , β ( 1 ) ) + b n ( M ( 1 ) , µ ( 0 ) , σ ( 0 ) , γ ( 0 ) , β ( 0 ) ) . M(2)= bn(M(1)∗ W(3), µ(3), σ(3), γ(3), β(3))+ bn(M(1)∗ W(1), µ(1), σ(1), γ(1), β(1))+ bn(M(1), µ(0), σ(0), γ(0), β(0)) . M(2)=bn(M(1)∗W(3),µ(3),σ(3),γ(3),β(3))

最低0.47元/天 解锁文章
【论文阅读】RepVGG: Making VGG-style ConvNets Great Again
hu_yinghui的博客
10-06 893
【论文阅读】RepVGG: Making VGG-style ConvNets Great Again 提出了一种类似VGG的推理时间体，仅由3×3卷积和ReLU的堆栈组成，而训练时间模型具有多分支拓扑。这种训练时间和推理时间结构的解耦是通过结构重新参数化技术实现的，因此该模型被命名为RepVGG，模型的运行速度比ResNet-50快83%，比ResNet-101快101%，具有更高的精度，与最先进的模型（如EfficientNet和RegNet）相比，显示出良好的精度-速度权衡。
【网络理解】RepVGG: Making VGG-style ConvNets Great Again
zengwb的博客
01-15 2166
系列文章目录 提示：这里可以添加系列文章的所有文章的目录，目录需要自己手动添加 例如：第一章 Python 机器学习入门之pandas的使用 提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录系列文章目录前言一、Netron模型可视化二、代码实现总结 前言 本文主要是对RepVGG的讲解 论文：https://arxiv.org/pdf/2101.03697.pdf GitHub：https://github.com/DingXiaoH/RepVGG 参考博客 一、Netron模型
＜论文翻译＞RepVGG: Making VGG-style ConvNets Great Again
行步至春深
03-22 1835
RepVGG:让VGG风格的卷积网络再一次伟大 作者 ![test](https://img-blog.csdnimg.cn/20210322111226782.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDk5NzgwMg==,size_16,color_FFFFFF,t_70) 摘要 我们提出了一个简单但功能强大的卷
RepVGG: Making VGG-style ConvNets Great Again(CVPR 2021)
Recursions的博客
10-10 501
（3）1x1卷积的表征能力弱于3x3卷积，因为前者可以看作一个有很多参数为0的3x3卷积，但是1x1 + 3x3的性能却好于3x3 + 3x3，一个强结构加一个弱结构大概率好于两个强结构相加。参考官方在ResNet-50/101的最后两个阶段使用Dilated Convolution，RepVGG的最后两个阶段使用Dilated Convolution。（1）推理时的等价性不代表训练时的等价性，直接训练一个 3x3 卷积最终也会得到同样形状的参数，虽然形状相同，但性能不同。
RepVGG（Re-parameterization VGG）: Making VGG-style ConvNets Great Again
胖胖大海的博客
02-06 1223
鉴于多分支模型训练性能好，推理性能差，单分支扁平化模型训练性能差，推理性能好的情况，将二者综合，试图构建一种网络模型，在模型训练阶段使用多分支训练获得更好的训练性能，在模型推理阶段将训练好的多分支模型恒等转换为单分支的扁平化模型，推理阶段的网络模型中只有3x3的卷积和ReLU激活这两种操作。这其中的核心问题就是如何把多分支的模型转换为一个单分支的模型？RepVGG里面把这个过程叫做结构重参数化技术。
论文阅读——《RepVGG: Making VGG-style ConvNets Great Again》
qq_36919342的博客
07-08 577
提出了一种简单但功能强大的卷积神经网络结构：ReVGG（没有任何分支，只使用3 × 3 conv和ReLU。）通过结构重新参数化来解耦训练时的多分支和推理时的平面体系结构，从而就能避免在训练时出现梯度消失的问题。 在ImageNet上，RepVGG达到80%以上的top-1精度。在NVIDIA 1080Ti GPU上，RepVGG模型的运行速度比ResNet-50快83%，比ResNet-101快101%，并且具有更高的精度，与最先进的模型如EfficientNet和RegNet相比，显示了良好的精度-速度
rep论文阅读4:RepVGG:Making VGG-style ConvNets Great Again
weixin_44600457的博客
05-06 882
利用结构重参数化“复兴”VGG式单路极简架构，一路3x3卷到底，在速度和性能上达到SOTA水平
【论文阅读】RepVGG: Making VGG-style ConvNets Great Again（CVPR2021）
络小绎
05-06 854
论文题目：RepVGG: Making VGG-style ConvNets Great Again 论文地址：https://arxiv.org/abs/2101.03697 代码地址：https://github.com/DingXiaoH/RepVGG 文章贡献： 1. 提出RepVGG网络，实现精度与速度的权衡； 2. 提出structural re-parameterization ，将多分支的训练模型解耦成普通结构用于推理； 3.展示了RepVGG在图像分类和语义分割方面的...
Backbone - RepVGG: Making VGG-style ConvNets Great Again
清欢
01-17 665
文章目录0. 前言1. 要解决什么问题2. 用了什么方法3. 效果如何4. 还存在什么问题&可借鉴之处 0. 前言 相关资料： arxiv github 论文解读（作者本人解读，其实已经说得很清楚了）：本文很多内容直接复制这一片。其实更建议大家看作者人本的文章，嘿嘿。 论文基本信息 领域：图像分类 作者单位：清华&旷视科技 发表时间：2021.1 一句话总结：解耦模型训练与模型部署，训练分支模型，经过等价转换变为单路模型，最终部署单路模型 1. 要解决什么问题 先定义下单
【RepVGG】《RepVGG：Making VGG-style ConvNets Great Again》
bryant_meng
10-17 664
CVPR-2021
SSD9的选择题们 较完整
09-01
DOC文档， SSD9的选择题， 比较完整
RepVGG: Making VGG-style ConvNets Great Again
03-08 961
提出了一个推理时类似VGG的只包含3X3卷积核Relu层但是训练时却是多分枝的RepVGG。它通过在参数化技术解耦了训练和推理，让模型拥有快速推理的同时也拥有高精度的表现。
RepVGG网络
qq_54372122的博客
04-10 516
作者单位：清华大学(丁贵广团队), 旷视科技(孙剑等人), 港科大, 阿伯里斯特威斯大学提出了一种简单而强大的卷积神经网络结构，其推理阶段是仅由3*3卷积和RELU组成VGG风格的结构，训练阶段则具有多分支结构。这种训练-推理的解耦是利用一种叫做“重参数化（re-parameterization）”的技术实现的，因此，该网络被称为RepVGG。在ImageNet上能够达到超过80%的top-1准确率，这是直通式网络第一次达到如此高的性能。
RepVGG: Making VGG-style ConvNets Great Again——让VGG风格的卷积神经网络再次伟大
Together_CZ的博客
12-04 1003
RepVGG: Making VGG-style ConvNets Great Again——让VGG风格的卷积神经网络再次伟大
(CVPR-2021)RepVGG：让 VGG 风格的 ConvNet 再次伟大
顾道长生的科研笔记
02-03 2827
我们提出了一种简单但功能强大的卷积神经网络架构，它具有类似 VGG 的推理时间主体，仅由3×33 \times 33×3卷积和 ReLU 堆栈组成，而训练时间模型具有多分支拓扑。这种训练时间和推理时间架构的解耦是通过结构重参数化技术实现的，因此该模型被命名为 RepVGG。据我们所知，在 ImageNet 上，RepVGG 达到了超过 80% 的 top-1 准确率，这对于普通模型来说是第一次。
[RepVGG] RepVGG：Making VGG-style ConvNets Great Again(CVPR.2021)
Ah丶Weii
03-04 568
paper：https://arxiv.org/abs/2101.0369 code：https://arxiv.org/abs/2101.0369 1. Motivation ​ 如今更复杂的卷积网络可以取得更大的精度，但是相对于简单的卷积网络来说，也有2种缺点，首先是多分支结构中复杂的设定，以及复杂卷积网络的计算资源的开销。 ​ 同时，其他simple ConvNets的性能并不能比得过complicated ConvNets。 2. Contribution 本文的贡献如下： 本文提出了Rep..
论文简读《RepVGG: Making VGG-style ConvNets Great Again》
grllery的博客
01-15 943
多分支的结构往往比单分支结构的性能要好，可能原因是`multi-branch`模型为众多浅层模型的隐式集合。因此作者提出在训练的时候使用`multi-branch`的结构，但是在部署的时候转换为单分支（不改变精度的情况下）。
Repvgg: Making vgg-style convnets great again
最新发布
07-23
**RepVGG: Making VGG-Style ConvNets Great Again** 是一种通过结构重参数化（Structural Re-parameterization）技术，将训练时的多分支复杂结构转换为推理时的单路VGG风格结构（仅含3×3卷积和ReLU）的卷积神经网络设计方法。以下是其核心思想与实现的分步解析： --- ### **1. 核心动机** - **VGG风格的优势**： - 结构简单（仅堆叠3×3卷积和ReLU），硬件友好（适合并行计算）。 - 但纯VGG网络在深层时易梯度消失，性能落后于ResNet等复杂结构。 - **现有结构的矛盾**： - 训练时需多分支结构（如ResNet的残差连接、Inception的多路径）提升梯度流动。 - 推理时多分支增加内存访问开销（MACs），降低实际速度。 - **RepVGG的解决方案**： - **训练时**：采用多分支结构（如ResNet的恒等映射+1×1卷积分支）。 - **推理时**：通过重参数化将多分支合并为单路3×3卷积，实现“训练复杂、推理简单”。 --- ### **2. 结构重参数化技术** #### **(1) 训练阶段的多分支设计** RepVGG的训练块（Block）包含三个并行分支： 1. **3×3卷积分支**：主路径，提取局部特征。 2. **1×1卷积分支**：调整通道数，增加非线性。 3. **恒等映射（Identity）分支**：短连接，缓解梯度消失。 **数学形式**： 输入 \( x \)，输出 \( y \) 为： \[ y = \text{ReLU}(\text{BN}_3(\text{Conv}_3(x)) + \text{BN}_1(\text{Conv}_1(x)) + \text{BN}_0(x)) \] 其中 \( \text{Conv}_3 \) 是3×3卷积，\( \text{Conv}_1 \) 是1×1卷积，\( \text{BN}_i \) 是批归一化层。 #### **(2) 推理阶段的单路转换** 通过以下步骤将多分支合并为单个3×3卷积： 1. **BN融合**： - 将每个分支的卷积（Conv）和批归一化（BN）合并为带偏置的卷积： \[ \text{Conv}_{\text{fused}} = \gamma \cdot \text{Conv} / \sqrt{\sigma^2 + \epsilon} + (\beta - \gamma \cdot \mu / \sqrt{\sigma^2 + \epsilon}) \] 其中 \( \gamma, \beta \) 是BN的缩放和平移参数，\( \mu, \sigma^2 \) 是均值和方差。 2. **1×1卷积→3×3卷积**： - 用零填充将1×1卷积的权重矩阵扩展为3×3（中心为原权重，四周为零）。 3. **恒等映射→3×3卷积**： - 将恒等映射视为一个特殊的3×3卷积，其权重矩阵中心为1，其余为零。 4. **分支合并**： - 将三个分支的3×3卷积权重和偏置相加，得到最终的3×3卷积： \[ W_{\text{final}} = W_3 + W_{1\to3} + W_{\text{id}\to3}, \quad b_{\text{final}} = b_3 + b_{1\to3} + b_{\text{id}\to3} \] **效果**： - 推理时模型变为纯VGG风格（仅3×3卷积+ReLU），速度更快（实测在GPU上比ResNet50快13%）。 - 参数和计算量与训练时相同（因重参数化无额外开销）。 --- ### **3. RepVGG的核心设计** #### **(1) 阶段式架构** - 类似ResNet，分多个阶段（Stage），每个阶段内堆叠相同结构的Block。 - **下采样**：通过步长为2的3×3卷积实现，同时通道数翻倍。 #### **(2) 通道数配置** - 浅层（如Stage1）通道数较少（如64），深层（如Stage4）通道数较多（如512）。 - **优势**：平衡计算量和表达能力，避免深层参数过多。 #### **(3) 训练技巧** - **数据增强**：采用AutoAugment或RandAugment提升泛化性。 - **标签平滑**：缓解过拟合（平滑系数0.1）。 - **混合精度训练**：加速训练并减少显存占用。 --- ### **4. 性能对比** | 模型 | 参数量（M） | Top-1准确率（ImageNet） | 推理速度（img/s, V100 GPU） | |---------------|-------------|--------------------------|-----------------------------| | ResNet50 | 25.6 | 76.5% | 1236 | | RepVGG-A0 | 8.3 | 72.4% | 3448（+179%） | | RepVGG-B1 | 51.8 | 78.4% | 1472（+19%） | | RepVGG-B3 | 103.9 | 80.5% | 831 | - **优势**：在相似参数量下，RepVGG的推理速度显著优于ResNet（尤其低参数量模型）。 - **代价**：训练时需多分支结构，可能增加内存占用（但可通过梯度检查点缓解）。 --- ### **5. 代码实现（PyTorch示例）** #### **(1) 训练块定义** ```python import torch import torch.nn as nn class RepVGGBlock(nn.Module): def __init__(self, in_channels, out_channels, stride=1): super().__init__() self.stride = stride self.conv1 = nn.Conv2d(in_channels, out_channels, 1, 1, 0, bias=False) self.conv3 = nn.Conv2d(in_channels, out_channels, 3, stride, 1, bias=False) self.bn1 = nn.BatchNorm2d(out_channels) self.bn3 = nn.BatchNorm2d(out_channels) self.bn_id = nn.BatchNorm2d(in_channels) if stride == 1 else None self.relu = nn.ReLU(inplace=True) def forward(self, x): id_out = 0 if self.stride == 1: id_out = self.bn_id(x) out3 = self.bn3(self.conv3(x)) out1 = self.bn1(self.conv1(x)) return self.relu(out3 + out1 + id_out) ``` #### **(2) 重参数化转换** ```python def repvgg_convert(block): # 融合BN到Conv def fuse_bn(conv, bn): w = conv.weight std = (bn.running_var + bn.eps).sqrt() t = (bn.running_mean - bn.bias) / std w_fused = w * (bn.weight / std).reshape([-1, 1, 1, 1]) b_fused = bn.bias + (bn.weight * t) - std * (w * t).sum([1, 2, 3]) return nn.Conv2d(conv.in_channels, conv.out_channels, 3, conv.stride, 1, bias=True) # 转换3×3分支 conv3_fused = fuse_bn(block.conv3, block.bn3) # 转换1×1分支为3×3 conv1_fused = nn.Conv2d(block.conv1.in_channels, block.conv1.out_channels, 3, 1, 1, bias=True) conv1_fused.weight.data.zero_() conv1_fused.weight.data[:, :, 1, 1] = block.conv1.weight.data conv1_fused.bias.data = block.bn1.bias - block.bn1.running_mean * block.bn1.weight / ( (block.bn1.running_var + block.bn1.eps).sqrt() ) # 合并分支 final_conv = nn.Conv2d( conv3_fused.in_channels, conv3_fused.out_channels, 3, conv3_fused.stride, 1, bias=True ) final_conv.weight.data = conv3_fused.weight.data + conv1_fused.weight.data if block.stride == 1: id_conv = nn.Conv2d(block.bn_id.num_features, block.bn_id.num_features, 3, 1, 1, bias=True) id_conv.weight.data.zero_() id_conv.weight.data[:, :, 1, 1] = 1.0 final_conv.weight.data += id_conv.weight.data final_conv.bias.data = conv3_fused.bias.data + conv1_fused.bias.data + block.bn_id.bias - block.bn_id.running_mean else: final_conv.bias.data = conv3_fused.bias.data + conv1_fused.bias.data return final_conv ``` --- ### **6. 挑战与改进方向** 1. **极深网络的训练稳定性**： - 超过50层的RepVGG可能需引入更多残差连接或梯度裁剪。 2. **移动端部署优化**： - 结合通道剪枝或量化（如INT8）进一步压缩模型。 3. **自适应结构**： - 根据任务动态调整分支数量（如浅层用1×1分支，深层用恒等映射）。 ---
评论 3
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值