感知机的暴力实现

下面是机器学习的《监督式学习》课程的一篇试读文章，进行了一下重新排版，然后展示在这里。由于格式的限制，缺少了一些习题、可运行的代码、证明、注释等，可能会导致解释差强人意，所以介意的同学可以直接访问感知机的暴力实现，以获得最佳的阅读体验。

1 寻找合适的和

简单来说，感知机就是要找到一条直线（或者说超平面），将两类点分开（下图中的为横坐标，为纵坐标）：

 

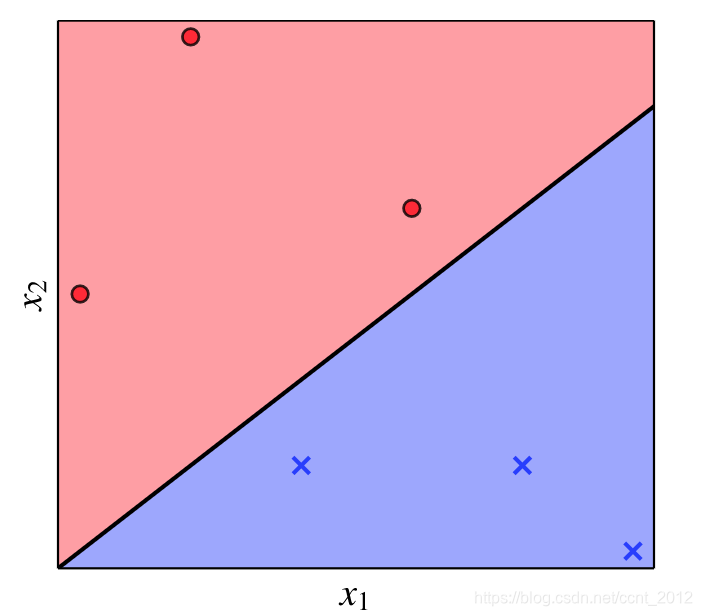
我们知道，直线（或者超平面）的方程为（下面的）：

本文就来介绍感知机如何通过一种看似暴力的方法来寻找合适的和，从而找到将两类点分开的直线（或者超平面）。

2 前置结论

首先我们要知道一些前置的结论，下面一一来介绍。

2.1 点积的正负与夹角的大小

根据点积的知识，可以知道点积的正负与夹角的大小如下：

 

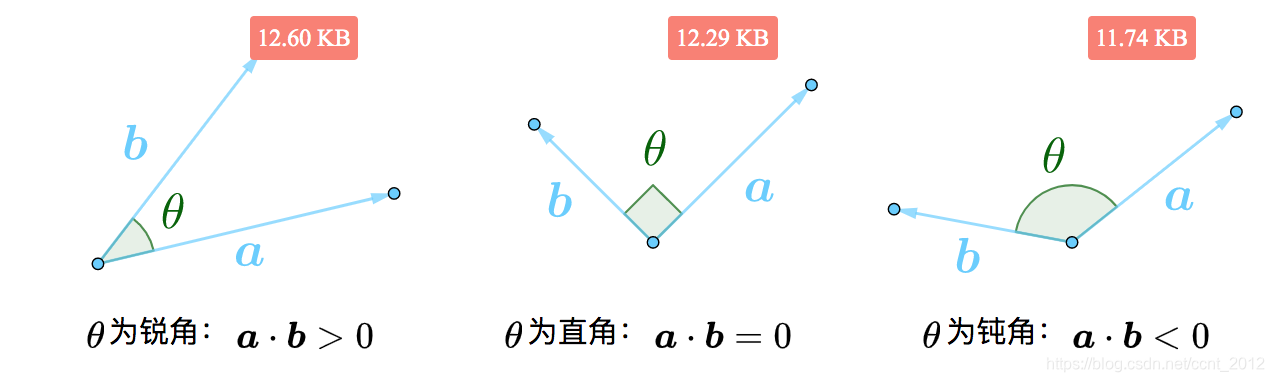
2.2 法向量

对于n维空间中的超平面而言，总是其法向量，即：

比如二维空间中，是一条直线，就垂直于该直线：

 

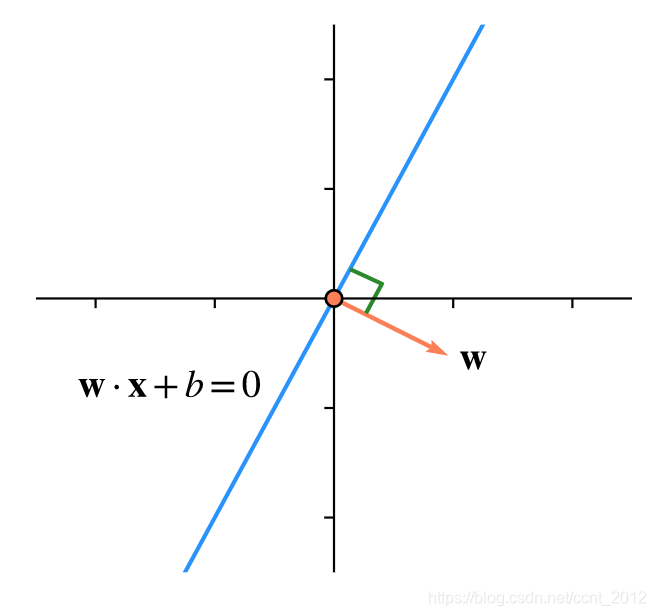
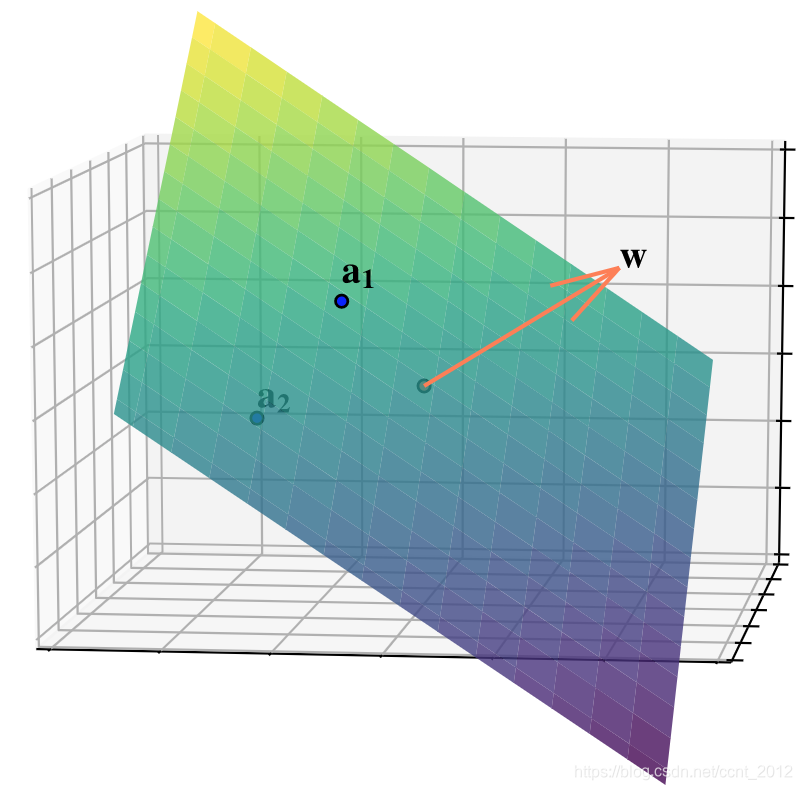
同样的道理，在三维空间中是一个平面，是该平面的法向量：

 

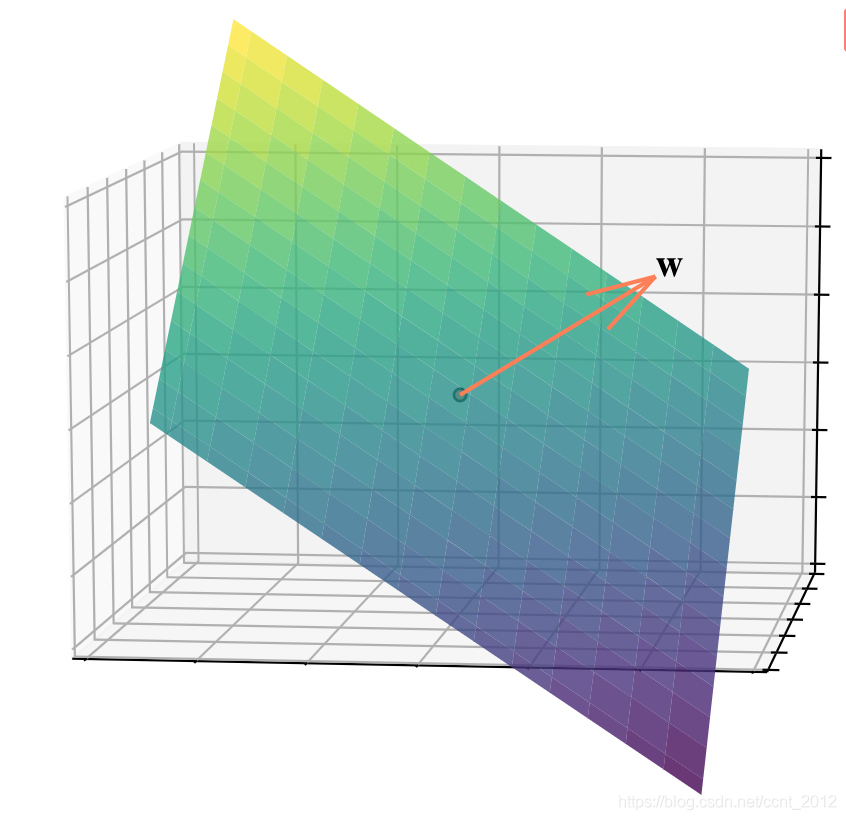
2.3 超平面的两侧

n维空间中的向量与超平面的关系为：

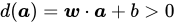• ：在超平面的法向量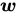所指的一侧

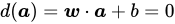• ：在超平面上

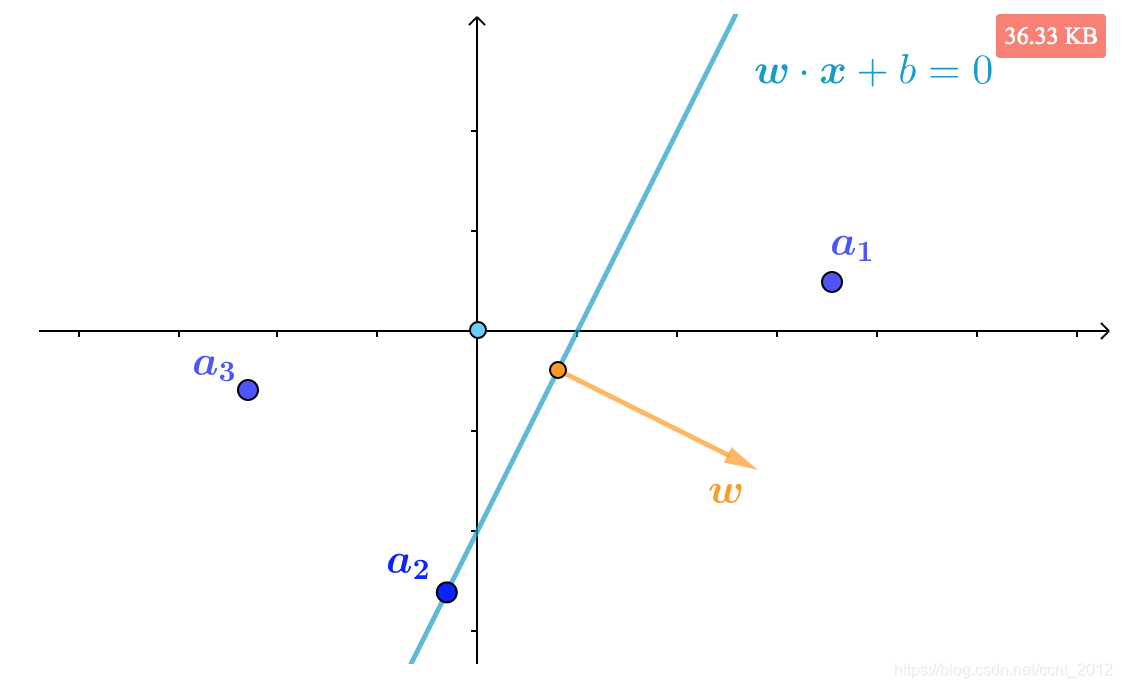
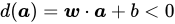• ：在超平面的法向量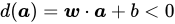所指的另外一侧

比如二维空间中的直线周围有三个向量：

根据上述结论可得：

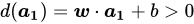• ：在直线的法向量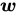所指的一侧

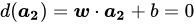• ：在直线上

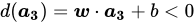• ：在直线的法向量所指的另外一侧

三维空间也是一样的，假设平面周围有两个向量：

根据上述结论可得：

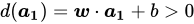• ：在平面的法向量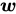所指的一侧

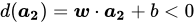• ：在平面的法向量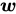所指的另外一侧

3 对错的判断

讲了这么多前置，下面开始介绍感知机的暴力实现。第一个问题是，要能判断找到的超平面的对错。

3.1 随便找的直线

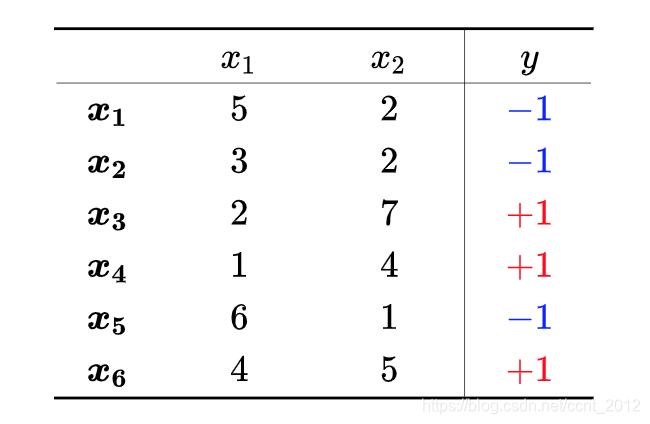
下面是用来作例子的数据集，其中为某点的作用，对应的y表示该点的类别：

3.2 是否分对

下面来判断该直线的对错。我们希望标签的特征向量在直线法向量所指的一侧，而的特征向量在法向量所指的另一侧。据此，上图中分对的点为、、、，根据上面“超平面的两侧”的介绍，可知它们是有共同特征的：

同理，分错的点、也是有共同特征的（分错边或者分到了边界线上都算错）：

3.3 小结

综上，判断对错的标准就是：

• 分对：

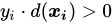
• 分错：

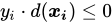
如果所有的都分对了，那么就说明是正确的超平面。

4 错误的纠正

前面看到、分错了，所以超平面是错误的，需要纠正。本节用两个二维空间中例子来说明纠错的思路，当然这些推论也是适用于n维空间的。

4.1 拉近

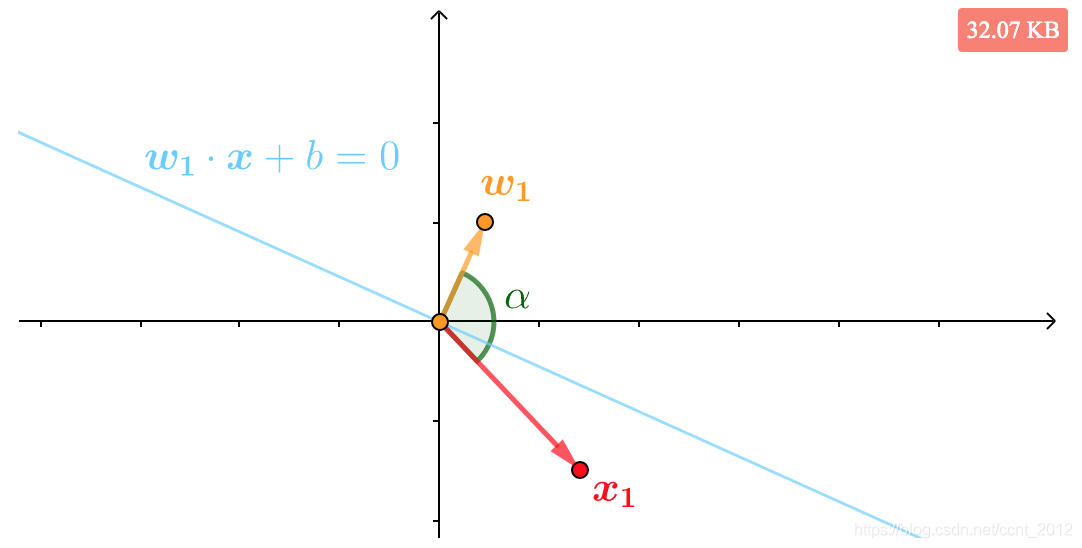
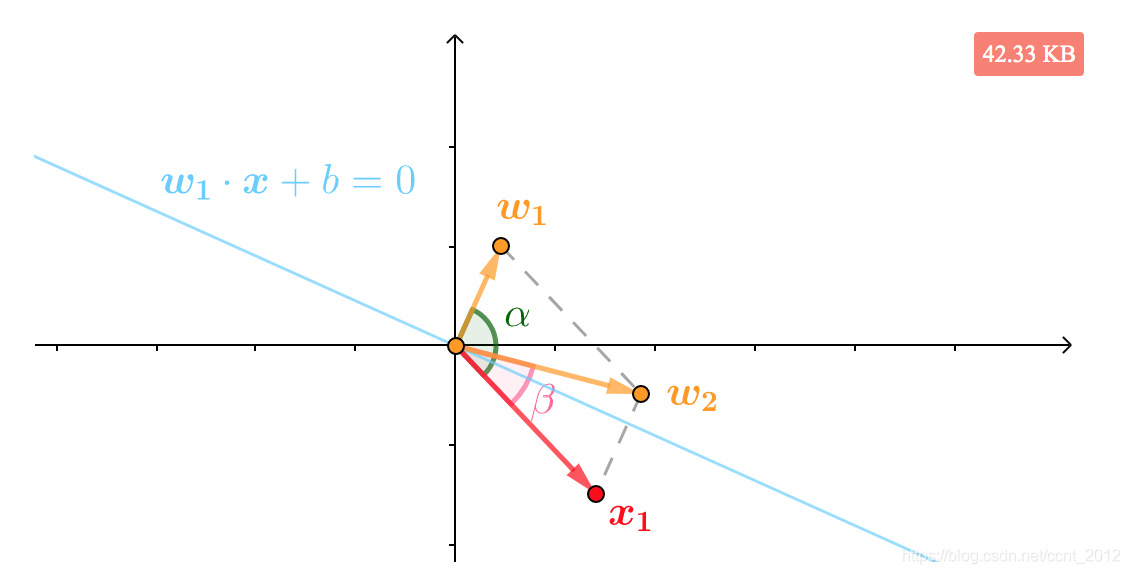
比如下面是标签的，它被错分到了直线的法向量所指另一侧，或者说本来和的夹角应该是锐角的，现在却是钝角：

那就想办法将法向量拉近一些。根据向量加法的平行四边形法则，可以看到就是和夹角更小的向量：

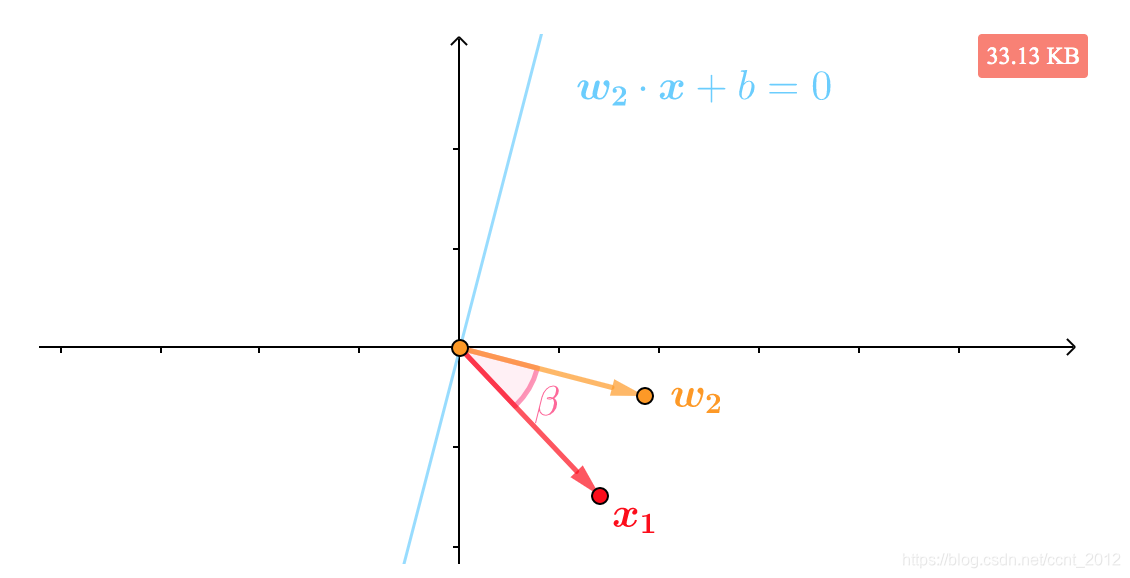
所以用为法向量，直线方程被纠正为，此时就可以正确分类：

4.2 推远

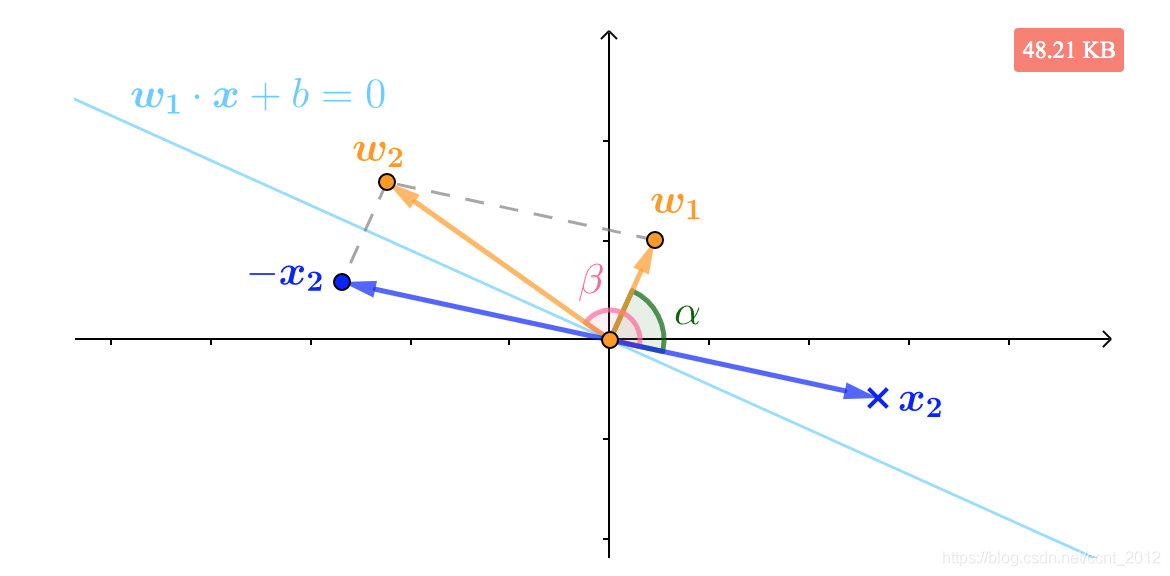
而下面是标签的被错分了，我们希望将法向量推远一点，同样根据向量加法的平行四边形法则，可以看到就是和夹角更大的向量：

所以用为法向量，直线方程被纠正为，此时就可以正确分类：

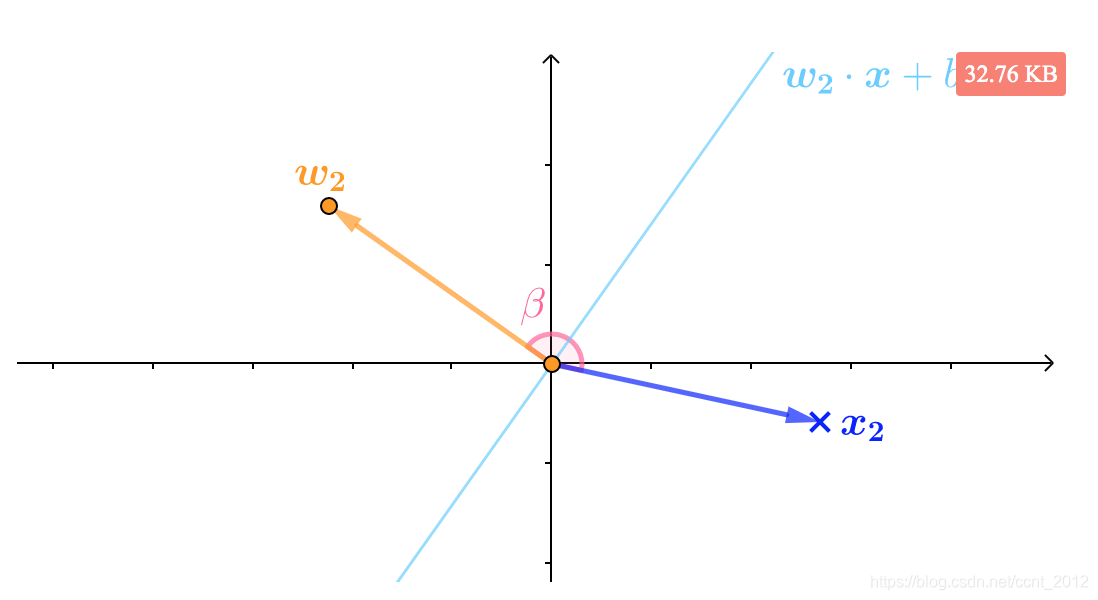
4.3 小结

总结下，当标签为的被错分时，也就有

此时，只需要令，就可以得到修正后的：

下面给一个例子来进一步说明该结论。

4.4 错误纠正的例子

例  如下图所示：

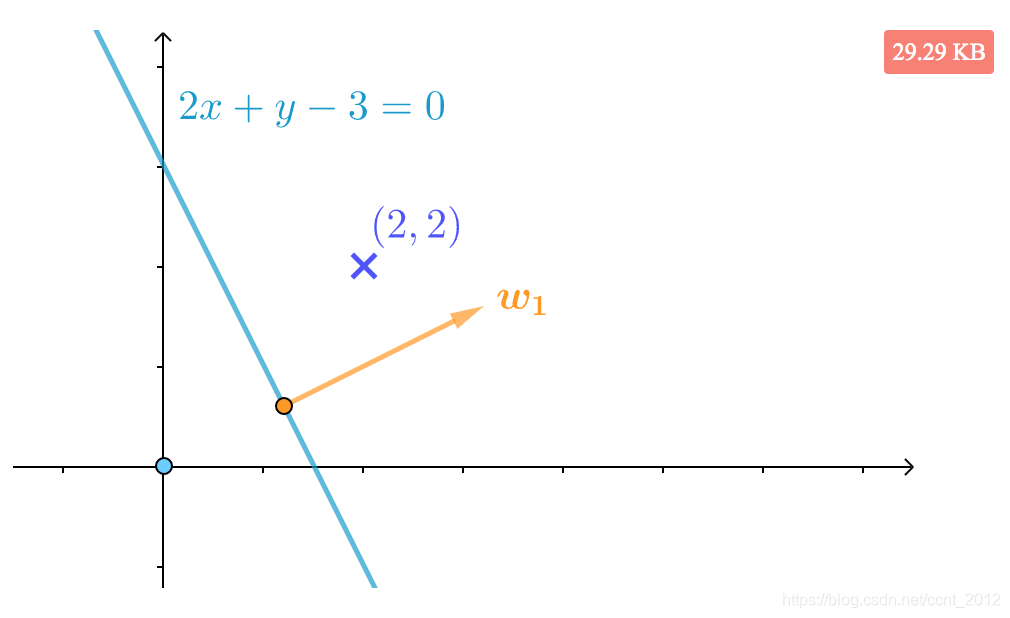
标签为的特征向量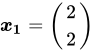分错了吗？如果分错又如何纠正？

解  通过看图，或者进行计算（该直线的法向量为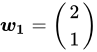），都可以发现分错了：

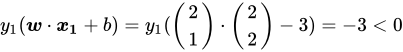
应该将法向量推远一点，修正后为：

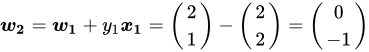
修正后的直线为，从夹角来看，修正后的法向量更远了：

5 找到决策边界

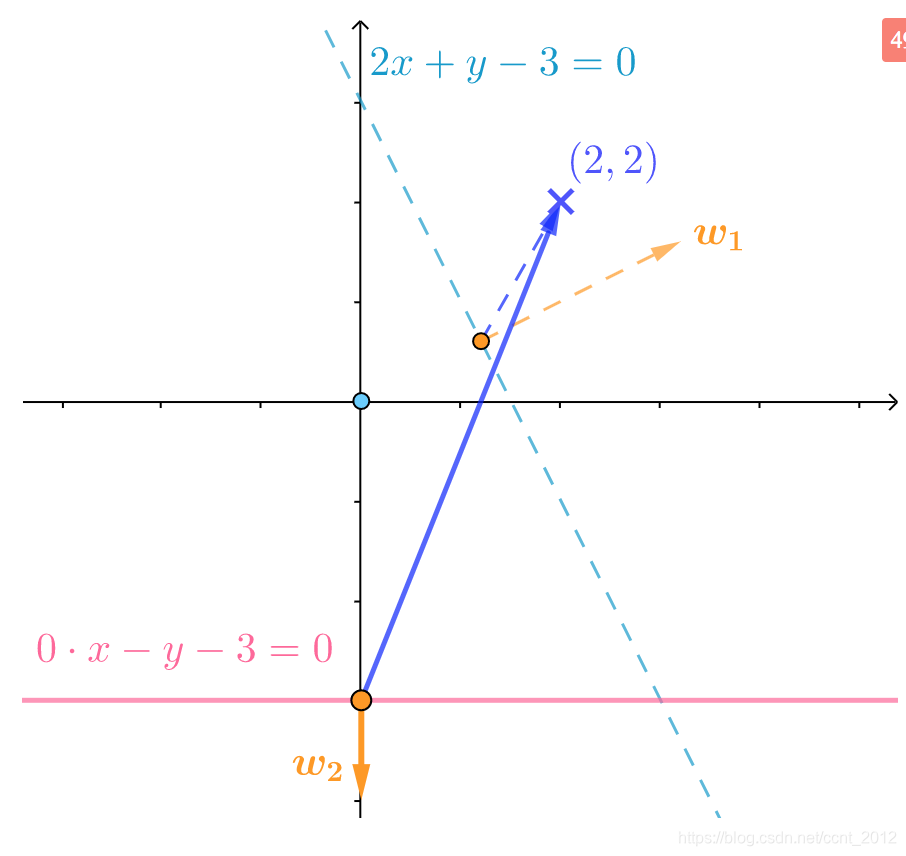
好了，现在具备需要的知识了，让我们来为、纠错。按顺序来吧。

5.1 的纠错

只需要令就可以得到新的超平面：

纠错后，对了。

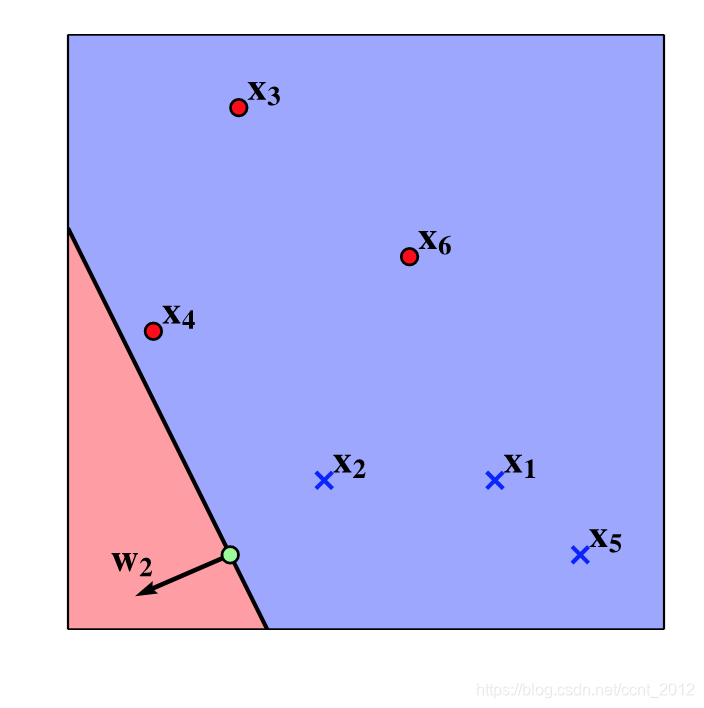
5.2 持续纠错

可是，原本没有错的却错了，令进行纠错；然后又错了，继续：

 

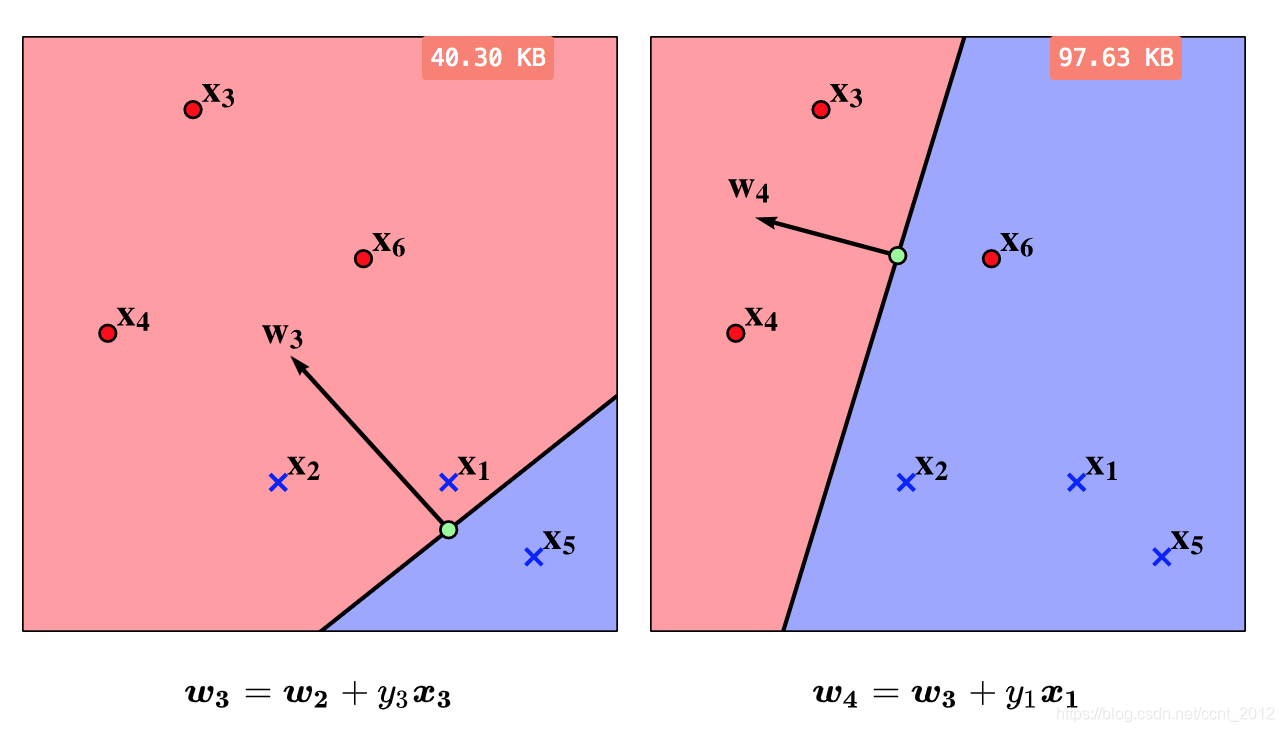
5.3 找到决策边界

还有错，还得继续：

 

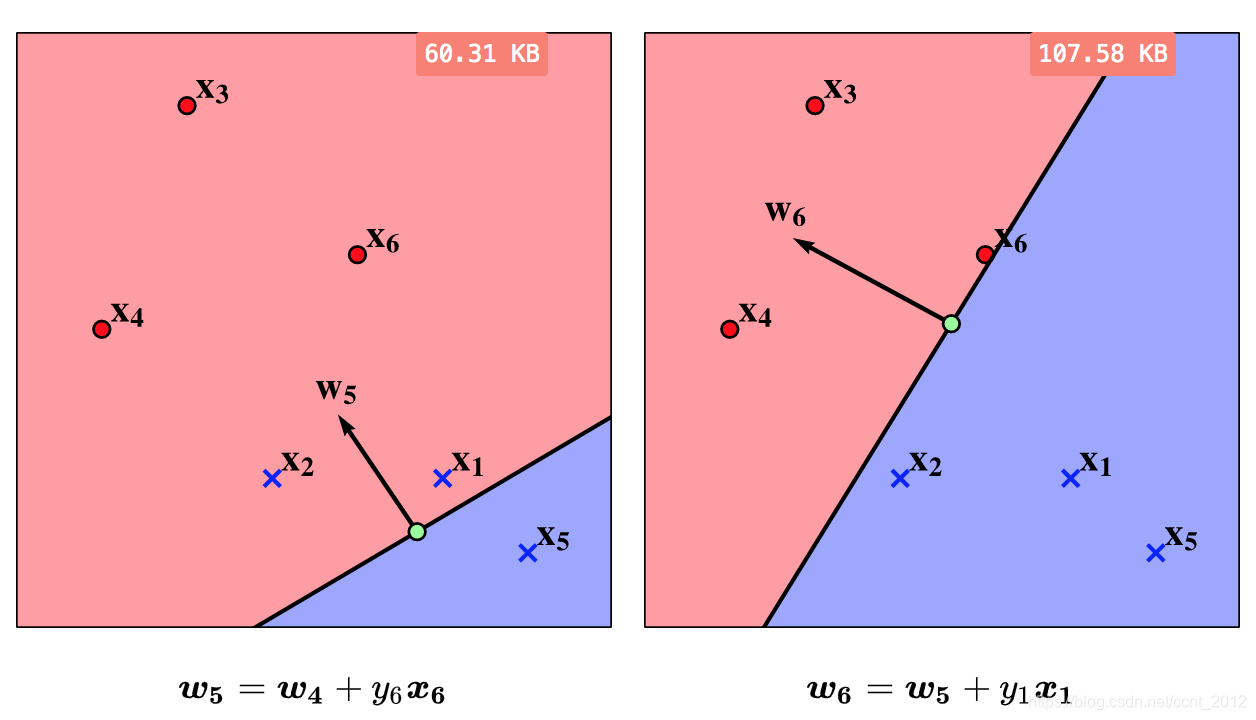
最后，法向量为的直线将所有的点正确分开，这就是感知机的暴力实现所要寻找的决策边界。

6 算法规范化

刚才介绍的算法一开始随机找了个超平面，实在太暴力了，下面来规范一下：

        （1）令权重向量和都为0：

所以初始函数为：

        （2）顺序遍历数据集，从中得到。

        （3）如果分错了，即 

则进行更正（因为刚开始，不更正的话，超平面的截距就一直是0，导致的后果是有可能不能将数据分开）：

        （4）转至（2），直到找到合适的和，使得对于所有的都满足：

此时可以说，该超平面将数据分为了两类。

6.1 实现

语言描述的算法可能有歧义，下面是按照上面步骤实现的代码，可以帮助同学们精确理解感知机的暴力实现：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Perceptron
from matplotlib.colors import ListedColormap

# 初始化 w 和 b，np.array 相当于定义向量
w, b = np.array([0, 0]), 0 

# 定义 d(x) 函数
def d(x):
    return np.dot(w,x)+b # np.dot 是向量的点积

# 历史信用卡发行数据
# 这里的数据集不能随便修改，否则下面的暴力实现可能停不下来
X = np.array([[5,2], [3,2], [2,7], [1,4], [6,1], [4,5]])
y = np.array([-1, -1, 1, 1, -1, 1])

# 感知机的暴力实现
is_modified = True # 记录是否有分错的点
while is_modified: # 循环，直到没有分错的点
    is_modified = False

    # 顺序遍及数据集 X
    for xi, yi in zip(X, y):
        # 如果有分错的
        if yi*d(xi) <= 0:
            # 更新法向量 w 和 b
            w, b = w + yi*xi, b + yi
            is_modified = True
            break

# 下面是绘制的代码，主要展示暴力实现的结果，看不懂也没有关系
def make_meshgrid(x, y, h=.02):
    """Create a mesh of points to plot in

    Parameters
    ----------
    x: data to base x-axis meshgrid on
    y: data to base y-axis meshgrid on
    h: stepsize for meshgrid, optional

    Returns
    -------
    xx, yy : ndarray
    """
    x_min, x_max = x.min() - 1, x.max() + 1
    y_min, y_max = y.min() - 1, y.max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    return xx, yy

def plot_contours(ax, clf, xx, yy, **params):
    """Plot the decision boundaries for a classifier.

    Parameters
    ----------
    ax: matplotlib axes object
    clf: a classifier
    xx: meshgrid ndarray
    yy: meshgrid ndarray
    params: dictionary of params to pass to contourf, optional
    """
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    out = ax.contourf(xx, yy, Z, **params)
    return out

# 训练 skrlearn 中的感知机，这里是为了借用该感知机的接口，便于绘制决策区域
clf = Perceptron().fit(X, y)
# 根据上面暴力实现得到的 w 和 b 来修改感知机
clf.coef_[0][0], clf.coef_[0][1], clf.intercept_[0] = w[0], w[1], b

# 设置字体大小
plt.rcParams.update({'font.size': 14})
# 设置画布和坐标系
fig, ax = plt.subplots(figsize = (6, 3), nrows=1, ncols=1)
fig.subplots_adjust(left=0.25, right=0.75, top=0.999, bottom=0.001)
ax.set_xticks(()),ax.set_yticks(())

cm = ListedColormap(('blue', 'red'))
markers = ('x', 'o')

# 决定绘制区域的大小
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())

# 绘制决策区域
plot_contours(ax, clf, xx, yy, cmap=cm, alpha=0.4)

# 绘制决策直线
lx = np.linspace(xx.min(), xx.max())
ly = - w[0] / w[1] * lx  - b / w[1]
ax.plot(lx, ly, 'k-')

# 根据类别不同，绘制不同形状的点
vmin, vmax = min(y), max(y)
for cl, m in zip(np.unique(y), markers):
  ax.scatter(x=X0[y==cl], y=X1[y==cl], c=y[y==cl], alpha=1, vmin = vmin, vmax = vmax, cmap=cm, edgecolors='k', marker = m)

plt.show()