为什么要引入矩阵这个数学工具？它能简化哪些不用矩阵会复杂的问题？

之前在“为什么学习线性代数”中宽泛地谈过我们需要矩阵的原因，本文这里再介绍一个我们课程《监督式学习》中通过矩阵来提升运算效率的例子。

先简单介绍下，之前在“如何理解线性回归”中介绍过线性回归的方法（简称为“老方法”），当特征较多时老方法效率很低（比如下文会提到的波士顿房价数据集），修改为矩阵算法之后效率会提高非常多倍：

下面就来解释其中的细节，文中有一些复杂的公式，忽略应该也不会影响理解大意。

1 线性回归

既然是和老方法比较，那么先简单复述下“如何理解线性回归”中介绍的老方法，需要了解细节的可以点击该链接回看。如果知道的可以跳到下一节“效率问题”。

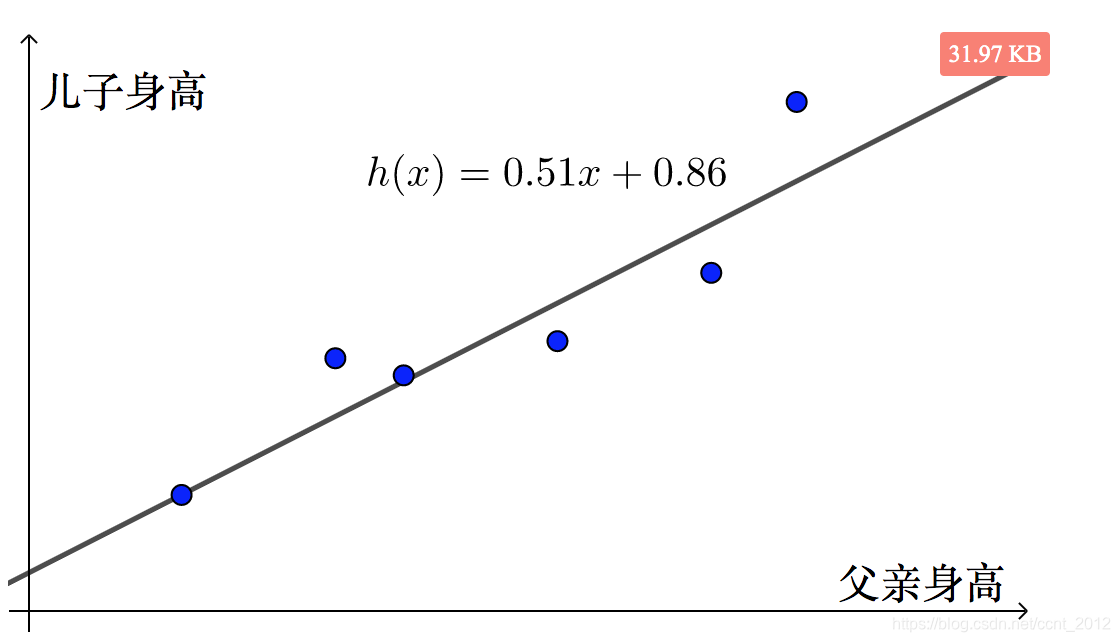
首先，回归就是根据数据集，拟合出近似的曲线，而像下列右图一样拟合出来是直线的就称为线性回归：

 

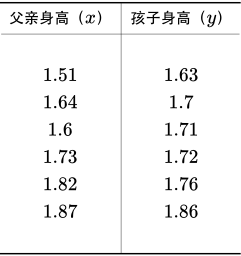
比如父子身高数据集：

 

我们通过最小二乘法来拟合直线，即假设要求的直线为，对于某父亲身高，该直线给出的和真实的儿子身高是存在距离的，这个距离也称为点与直线的误差，用两者差的平方来表示：

 

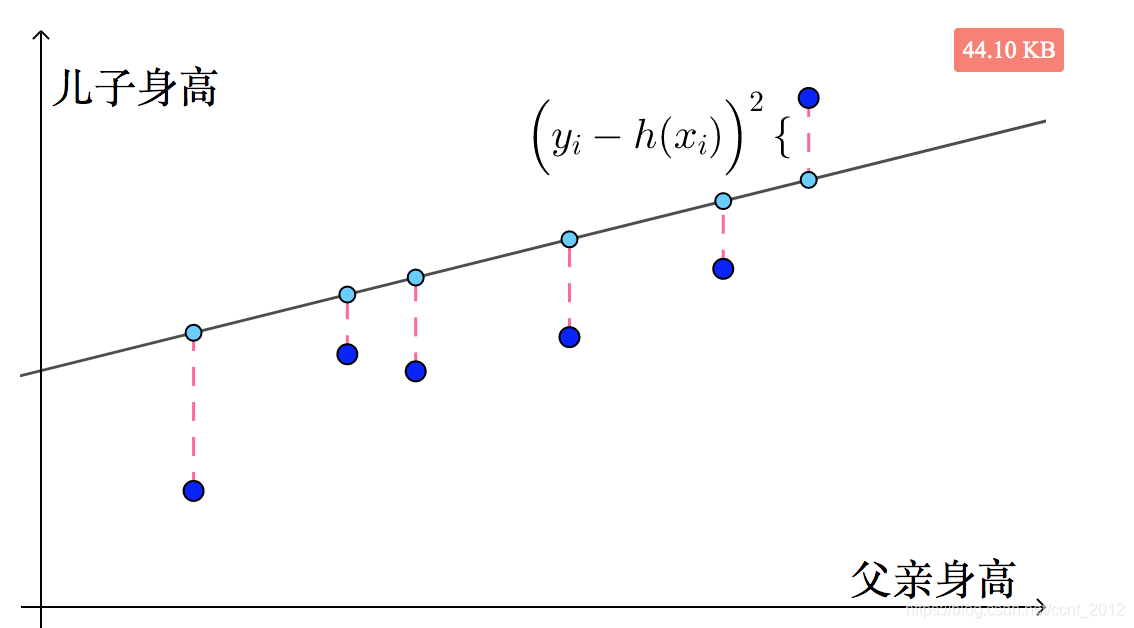
将数据集中所有点与该直线的误差加起来，再进行算术平均就是该直线在数据集上的经验误差：

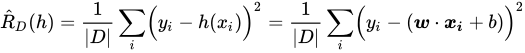
然后通过求该经验误差的最小值来拟合直线，即通过解下面方程组求出直线的参数：

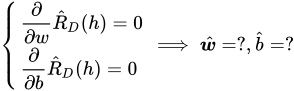
根据上面描述的数学原理，可以借助 Python 来求出 w 和 b：

from sympy import symbols, diff, solve
import numpy as np

# 数据集 D
X = np.array([1.51, 1.64, 1.6, 1.73, 1.82, 1.87])
y = np.array([1.63, 1.7, 1.71, 1.72, 1.76, 1.86])

# 构造经验误差函数
w, b = symbols('w b', real=True)
RDh = 0
for (xi, yi) in zip(X, y):
	RDh += (yi - (xi*w + b))**2
RDh *= 1/len(X)

# 对 w 和 b 求偏导
eRDhw = diff(RDh, w)
eRDhb = diff(RDh, b)

# 求解方程组
ans = solve((eRDhw, eRDhb), (w, b))
print('使得经验误差函数 RD(h) 取最小值的参数为：{}'.format(ans))

上面代码运行后，可以解出以及，从而得到拟合的直线，即完成线性回归：

 

2 效率问题

上面的数据集只有特征只有一个，就是儿子的身高，当使用更多特征的数据集时，构造经验误差函数和求偏导就会出现效率问题。

该数据集总共有 506 条数据，每条数据对应一所房屋，每所房屋包含 13 个特征，标签是各个房屋的价格。下面展示该数据集的前五条（前面 13 列为特征，最后 1 列为价格）：

别管这些特征具体是什么，当尝试在该数据集上构造经验误差：

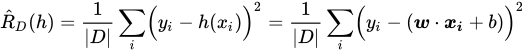
你会发现和都是 13 维的向量（因为每个向量包含了 13 个特征）：

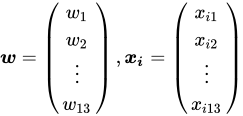
此时光是通过 sympy 构造经验误差函数运行就需要十多二十秒（ sympy 进行符号运算是非常慢的），同学可以拷贝到本地运行试试：

from sympy import symbols, diff, solve
import numpy as np
from sklearn.datasets import load_boston
import timeit

# 加载波士顿数据集
X, y = load_boston(return_X_y=True)

# 开始计时
start = timeit.default_timer()

# 构造经验误差函数
w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, b = symbols('w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 w13 b', real=True)
w = (w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13)
RDh = 0
for (xi, yi) in zip(X, y):
	err = 0
	err += yi - b
	for (xii, wi) in zip(xi, w):
		err -= xii*wi
	RDh += err**2
RDh *= 1/len(X)

# 停止计时，打印耗时
stop = timeit.default_timer()
print('耗时 {:.2f} 秒'.format(stop - start))

更不要说之后求偏导、解方程组了。所以需要寻找对于计算机来说更高效的算法。

3 最小二乘法的矩阵算法

上面解释了，通过解下列方程组来完成线性回归实在太低效了：

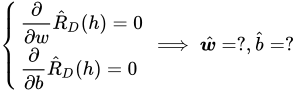
如果引入矩阵，可以将上面方程组的求解等价地转换为如下形式（其中被称为伪逆，直接被 numpy 支持，可以简化我们的代码，并且被包含到了，其中的细节不再赘述）：

矩阵算法非常高效，可以轻松完成对波士顿房价数据集的线性回归：

import numpy as np
from sklearn.datasets import load_boston

# 读取波士顿房价数据集
X0, y = load_boston(return_X_y=True)

# 构造 X，即给 X0 增加一行 1
ones = np.ones(X0.shape[0]).reshape(-1, 1)
X = np.hstack((ones, X0))

pinvX = np.linalg.pinv(X)   # 计算伪逆
w = pinvX @ y               # 最小二乘法的矩阵算法

# 打印结果
with np.printoptions(precision=3, suppress=True):	# 设置输出格式
	print('结果：w = {} 。'.format(w))

上面代码求出来的，除了第一项是之外，其余每一项代表了房屋某个特征的权重（因为有 13 个特征没有办法可视化，通过阅读各个特征的权重也可以对该结果了解一二）：

从上表中可以看出，对房价正面影响最大的是 RM（每处住房的平均房间数）以及 CHAS（是否在查理斯河边），负面影响最大的则是 NOX （一氧化氮浓度，即空气质量），这都符合我们对房屋价格的直觉。