LCA - Lowest Common Ancestor

LCA - Lowest Common Ancestor

https://www.luogu.com.cn/problem/SP14932

题目描述

A tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree. - Wikipedia

The lowest common ancestor (LCA) is a concept in graph theory and computer science. Let T be a rooted tree with N nodes. The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants (where we allow a node to be a descendant of itself). - Wikipedia

Your task in this problem is to find the LCA of any two given nodes v and w in a given tree T.

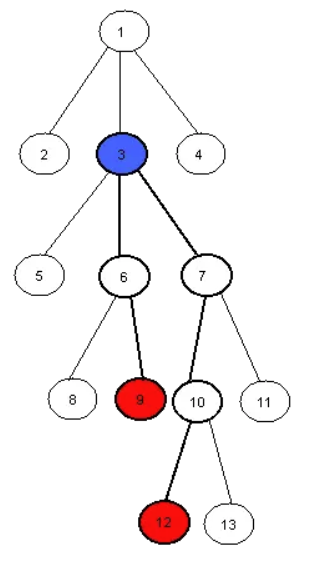
For example the LCA of nodes 9 and 12 in this tree is the node number 3.

Input

The first line of input will be the number of test cases. Each test case will start with a number N the number of nodes in the tree, 1 <= N <= 1,000. Nodes are numbered from 1 to N. The next N lines each one will start with a number M the number of child nodes of the Nth node, 0 <= M <= 999 followed by M numbers the child nodes of the Nth node. The next line will be a number Q the number of queries you have to answer for the given tree T, 1 <= Q <= 1000. The next Q lines each one will have two number v and w in which you have to find the LCA of v and w in T, 1 <= v, w <= 1,000.

Input will guarantee that there is only one root and no cycles.

Output

For each test case print Q + 1 lines, The first line will have “Case C:” without quotes where C is the case number starting with 1. The next Q lines should be the LCA of the given v and w respectively.

Example

Input:

1
7
3 2 3 4
0
3 5 6 7
0
0
0
0
2
5 7
2 7

Output:

Case 1:
3
1

输入格式

无

输出格式

无

代码

倍增算法

#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
vector<int> dep;         // 存储深度
vector<vector<int>> fa;  // 存储跳跃点
vector<vector<int>> e;   // 存储边
void dfs(int x, int y) {
  for (int i = 1; i <= 9; i++) {
    fa[x][i] = fa[fa[x][i - 1]][i - 1];
  }

  for (auto i : e[x]) {
    dfs(i, x);
  }
}

int lca(int u, int v) {
  if (dep[u] < dep[v]) swap(u, v);

  for (int i = 9; i >= 0; i--) {
    if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];
  }
  if (u == v) return v;

  for (int i = 9; i >= 0; i--) {
    if (fa[u][i] != fa[v][i]) {
      u = fa[u][i];
      v = fa[v][i];
    }
  }
  return fa[u][0];
}

void solve() {
  int N;  // 节点数
  cin >> N;
  dep    = vector<int>(N + 1);
  fa     = vector<vector<int>>(N + 1, vector<int>(10, 0));
  e      = vector<vector<int>>(N + 1);
  dep[1] = 1;
  for (int i = 1; i <= N; i++) {
    int sonNum;  // 子节点数量
    cin >> sonNum;

    while (sonNum--) {
      int sonNode;
      cin >> sonNode;
      e[i].push_back(sonNode);
      fa[sonNode][0] = i;
      dep[sonNode]   = dep[i] + 1;
    }
  }

  dfs(1, 0);

  int queryNum;
  cin >> queryNum;  // 查询次数
  while (queryNum--) {
    int u, v;
    cin >> u >> v;
    cout << lca(u, v) << endl;
  }
}

int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int T;
  cin >> T;
  for (int i = 1; i <= T; i++) {
    cout << "Case " << i << ":" << endl;
    solve();
  }
  return 0;
}

tarjan算法

#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
vector<bool> vis;                      // 存储是否访问
vector<int> fa;                        // 存储父节点
vector<vector<int>> e;                 // 存储子节点
vector<vector<pair<int, int>>> query;  // 需要查询的
vector<int> ans;                       // 存储答案

int find(int x) {
  if (x == fa[x]) return x;
  return fa[x] = find(fa[x]);
}

void tarjan(int x) {
  vis[x] = true;

  for (auto son : e[x]) {
    if (!vis[son]) {
      tarjan(son);
      fa[son] = x;
    }
  }

  for (auto q : query[x]) {
    int y = q.first, id = q.second;
    if (vis[y]) {
      ans[id] = find(y);
    }
  }
}
void solve() {
  int N;  // 节点数
  cin >> N;
  fa = vector<int>(N + 1);
  e  = vector<vector<int>>(N + 1);
  query.resize(N + 1);
  vis = vector<bool>(N + 1, false);

  for (int i = 1; i <= N; i++) {
    fa[i] = i;
  }

  // 输入子节点
  for (int i = 1; i <= N; i++) {
    int sonNum;
    cin >> sonNum;
    while (sonNum--) {
      int sonNode;
      cin >> sonNode;
      e[i].push_back(sonNode);
    }
  }

  int queryNum;
  cin >> queryNum;
  ans = vector<int>(queryNum + 1);
  for (int i = 1; i <= queryNum; i++) {
    int u, v;
    cin >> u >> v;
    query[u].push_back({ v, i });
    query[v].push_back({ u, i });
  }

  tarjan(1);

  for (int i = 1; i <= queryNum; i++) {
    cout << ans[i] << endl;
  }
}

int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int T;
  cin >> T;
  for (int i = 1; i <= T; i++) {
    cout << "Case " << i << ":" << endl;
    solve();
  }
  return 0;
}