专业基本能力测试——西爱吃西
判断题
1-1

T
C语言的数组下标从0开始。
1-2

T
这是因为浮点数在计算机中的存储方式是有限的,可能会存在精度误差。因此,直接判断两个浮点数是否相等可能会出现错误的结果。应该使用一些特定的方法来比较浮点数,例如比较它们的差值是否小于一个很小的数,或者使用一些库函数来进行比较,这样可以避免因精度误差而导致的错误判断。
1-3

F
C语言程序区分大小写。

T
函数重载是指同一个函数名可以有多个版本,这些版本必须在参数个数或者参数类型上有所不同,与返回值无关。
1-5

T
重载不能改变运算符的优先级和结合性。
1-6

F
-
正确部分
派生类对象可以直接转换为基类对象:这部分是正确的。派生类对象可以直接赋值给基类对象,这种转换被称为“向上转换”或“上行转换”,是安全的,并且是自动进行的。
-
错误部分
基类对象可以直接转换为派生类对象:这部分是不正确的。基类对象不能直接转换为派生类对象。这种转换被称为“向下转换”或“下行转换”,需要进行类型检查,通常使用C++的dynamic_cast运算符。如果基类对象没有包含派生类对象的实际实例,这种转换是危险的,并且会失败。
1-7

T
与单继承中派生类的构造函数类似,多重继承派生类的构造函数不但要对派生类中新增成员完成初始化,还要依次对各基类的继承成员进行初始化。
1-8

T
局部变量可以和成员变量重名,不加this修饰时,优先使用最近的变量。
1-9

T
正确的。比如:
Student()
{
string name;
Student()
{
}
Student(string name)
{
this->name = name;
}
}
int main()
{
Student stuA = new Student("小明");
Student stuB = new Student("小王");
}
stuA和stuB的name是不同的值
1-10(?)

T
1-11

T
所有NP完全问题(NP-Complete问题)都是NP问题。这是因为NP完全问题是NP问题中的一个子集,并且具有额外的性质:每个NP完全问题都可以被归约(Reduction)到另一个NP完全问题。因此,所有NP完全问题必然也是NP问题。
1-12

F
对于频繁进行不同下标元素的插入和删除操作,链式存储结构通常会比顺序存储结构更好。原因是:
- 顺序存储结构(如数组)在插入或删除元素时,可能需要移动大量元素,以保证元素的连续性。这种操作的时间复杂度通常为 O(n),尤其是当插入或删除的位置接近数组的开始或中间时。
- 链式存储结构(如链表)则不需要移动其他元素,只需要调整相邻节点的指针,因此插入和删除操作通常可以在 O(1) 时间内完成,前提是你已经定位到正确的位置。
1-13

T
栈是先进后出的线性表。
1-14

F
队列是先进先出的线性表。
单选题
2-1

A
标识符的组成:
- 字母(A-Z, a-z):
- 标识符可以包含字母,通常不区分大小写(但有些语言如Java区分大小写)。
- 数字(0-9):
- 标识符可以包含数字,但不能以数字开头。
- 下划线(_):
- 下划线是有效的标识符字符,通常用于提高代码的可读性,比如
my_variable。
- 下划线是有效的标识符字符,通常用于提高代码的可读性,比如
不能作为标识符的内容:
- 保留字/关键字:
- 标识符不能是语言的保留字或关键字。例如,C、C++中的
int、while,Java中的public、class,Python中的def、for都不能用作标识符。
- 标识符不能是语言的保留字或关键字。例如,C、C++中的
- 空格、标点符号和特殊字符:
- 标识符中不能包含空格、运算符、标点符号(如
+,-,*,&),以及其他特殊字符(如@,#,$等)。
- 标识符中不能包含空格、运算符、标点符号(如
- 其他语言限制:
- 某些语言可能有额外的规则,例如C++标准中有对标识符命名的长度和使用某些字符的限制。
2-2

A
解析:
-
函数的定义不能嵌套:
- 在大多数编程语言中,函数的定义不能嵌套在其他函数内部。也就是说,你不能在一个函数内部再定义另一个函数。比如,在C、C++、Java和Python等语言中,函数定义通常是独立的,并且只能在文件的作用域中(或类的作用域中)定义,而不能在另一个函数的定义内部定义。
-
函数的调用可以嵌套:
- 函数的调用可以嵌套,即在一个函数的实现中可以调用其他函数,甚至可以调用自身(递归)。嵌套调用是常见的编程模式。例如,函数A可以调用函数B,而函数B也可以调用函数C,函数A和B的调用关系就是嵌套的。
示例:
-
函数定义不能嵌套(不允许在一个函数内部定义另一个函数):
// 错误示范 void outerFunction() { void innerFunction() { // 不能在函数内部定义另一个函数 // ... } } -
函数调用可以嵌套(可以在一个函数中调用其他函数):
// 正确示范 void foo() { bar(); // foo调用bar } void bar() { // ... }
总结:函数的定义通常不能嵌套,而函数的调用(包括嵌套调用)是允许的。
2-3

D
选项A:break语句不仅可以用于switch语句,还可以用于循环语句(如for、while等),以跳出循环。
选项B:default是可选的,即使在switch语句中没有default子句,语法依然是合法的。
选项C:虽然在大多数情况下,break语句与switch语句中的case配对使用以防止“贯穿”(fall-through),但它不是必须的。可以省略break语句以使程序继续执行后续的case块。
选项D:如上所述,break语句在switch语句中是可选的,而不是必须的。省略它会导致程序“贯穿”到下一个case块。
2-4
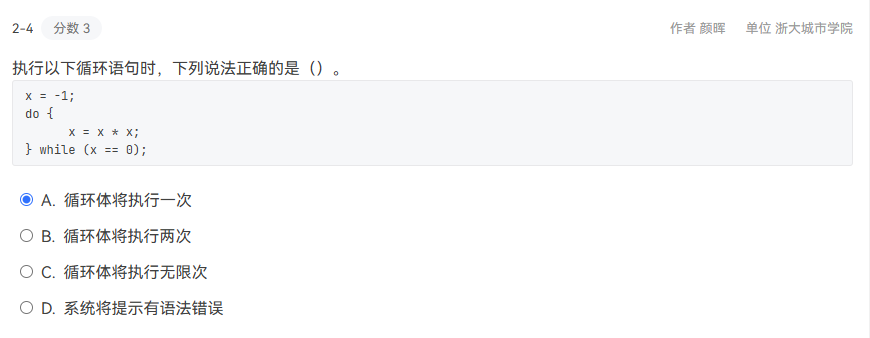
A
由于是do-while,不管条件如何会先执行一遍循环,执行x=x*x后x的值变为1,此时不符合判断条件x==0,跳出循环,所以只执行一次。
2-5

D
结构程序设计的三种结构是:顺序结构、选择结构、循环结构。
2-6

D
解析:
-
A. 指针可以进行加、减等算术运算:
这是正确的。在C/C++等语言中,指针支持加法和减法运算。例如,你可以增加指针的值来让它指向下一个内存单元,或减去一个值来让它指向前一个内存单元。指针算术运算通常是基于数据类型大小的。 -
B. 指针中存放的是地址值:
这是正确的。指针变量存储的是一个内存地址,该地址指向一个具体的数据对象或函数。 -
C. 指针是一个变量:
这是正确的。指针是一个变量,和其他变量一样,它也有自己的存储空间,并且存储的是一个地址。 -
D. 指针变量不占用存储空间:
这是错误的。指针变量本身是一个变量,它占用一定的存储空间。在大多数现代系统中,指针通常占用 4 或 8 个字节(具体大小取决于系统架构,例如32位系统上通常是4字节,64位系统上通常是8字节)。
因此,D 选项是错误的,指针变量和其他类型的变量一样,也需要占用存储空间。
2-7

B
A. 递归函数是自己调用自己。这个说法是正确的。
B. 递归函数的运行速度很快。这个说法是错误的。递归函数由于需要进行多次调用,运行速度通常较慢,尤其是在递归深度较大时。
C. 递归函数占用较多的存储空间。这个说法是正确的。因为每次递归调用都会占用堆栈空间,因此递归函数通常比迭代方法占用更多的存储空间。
D. 递归函数的运行速度一般比较慢。这个说法是正确的。
所以,正确答案是 B。
2-8
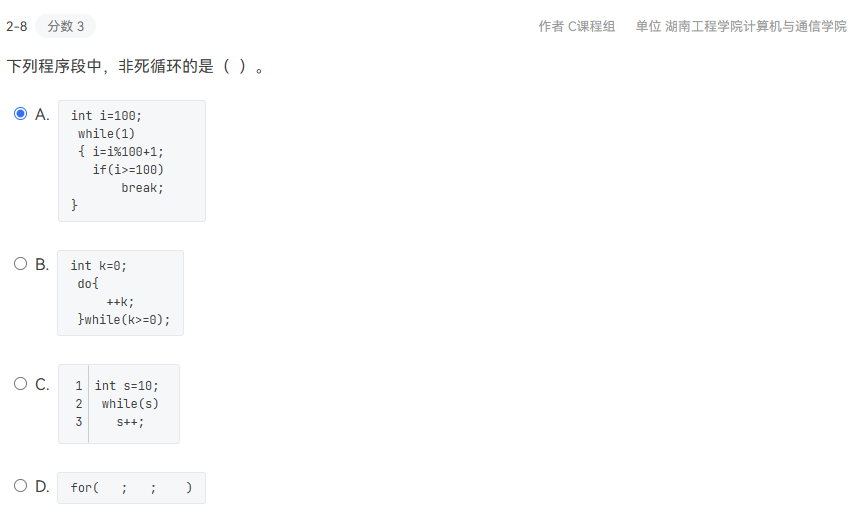
A。
当i为99时,i%100+1为100,结束循环。
2-9

D
面向对象程序设计通过封装、继承和多态等特性,使得代码可以被复用,提高了开发效率和软件质量。这种编程范式有助于创建模块化、可扩展和易于维护的软件系统。
2-10

A
2-12
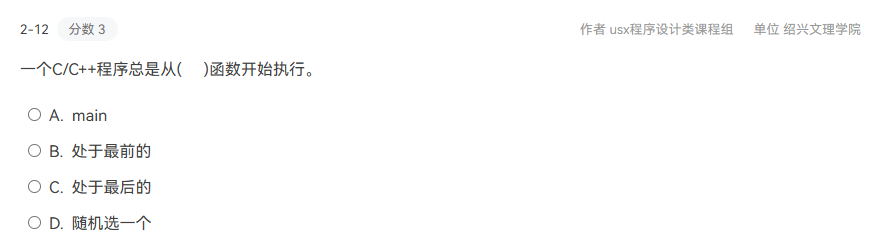
A。main 函数是程序的入口点,每个C/C++程序都必须包含一个 main 函数,不然程序无法编译和执行。
2-13

C
2-14

D
具有以下形态:
- 一个根节点,左子树有两个节点。
- 一个根节点,右子树有两个节点。
- 一个根节点,左子树有一个节点,右子树有一个节点。
- 一个根节点,左子树有一个节点,左子树的右子树有一个节点。
- 一个根节点,右子树有一个节点,右子树的左子树有一个节点。
扩展:n个节点可以构造的二叉树形态数量:
f(n)=(2n)!(n+1)!n!
f(n) = \frac{(2n)!}{(n+1)!n!}
f(n)=(n+1)!n!(2n)!
2-15

C
二叉树高度的范围
计算具有 n 个节点的二叉树的高度可以从以下两个极端情况考虑:完全二叉树和链式二叉树(最坏情况)。
-
完全二叉树(最小):
- 在这种情况下,二叉树的高度是最小的。
- 完全二叉树的高度为 log2(n+1)\log_2(n+1)log2(n+1)(向上取整)或者log2(n)\log_2(n)log2(n)(向下取整再加1),因为完全二叉树的节点数量满足 20+21+...+2h=n2^0 + 2^1 + ... + 2^h = n20+21+...+2h=n,其中 h 是高度。
-
链式二叉树(最大):
- 这是最坏的情况,即所有的节点都只有一个子节点,形成一条直线。
- 在这种情况下,树的高度是最大的,等于 n,因为每个节点都加在前一个节点之上。
2-16
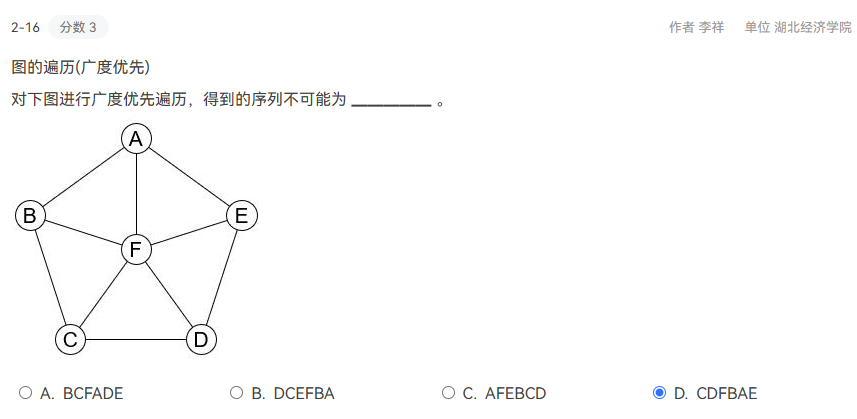
D
第一层:C
第二层:DFB
第三层:AE错误,因为第二层从D开始,所以第三层必须是与D相连的E开头,即EA
D选项应为:CDFBEA
2-17

B
A和D选项第一步就错误,第一步只能是从A节点开始
C选项第三个的D节点错误,必须还有C节点在D节点前面
2-18

D
具体步骤如下:
- S:将1入栈。
- X:将1出栈。
- S:将2入栈。
- S:将3入栈。
- X:将3出栈。
- S:将4入栈。
- X:将4出栈。
- X:将2出栈。
2-19

B
假设某个带头结点的单链表的头指针为 head,则判定该表为空表的条件是 head->next == NULL。因为带头结点的单链表中,头结点(head)本身并不存储有效数据,它只是一个指向链表第一个有效节点的指针。如果 head->next 为空,说明链表中没有有效节点,链表为空。
2-20

C
要将普通的中缀表达式转换为后缀表达式(也称为逆波兰表示法,RPN),可以使用一种名为“Shunting Yard”的算法,这是由计算机科学家Edsger Dijkstra发明的。以下是步骤:
- 初始化两个栈:一个操作符栈和一个输出栈。
- 从左到右遍历输入表达式中的每个字符:
- 操作数(数字或变量):直接放入输出栈。
- 左括号:放入操作符栈。
- 右括号:从操作符栈中弹出操作符,并将它们放入输出栈,直到遇到左括号(左括号不放入输出栈)。
- 操作符:处理操作符时,需要考虑操作符的优先级和栈中的其他操作符。
- 当操作符栈非空且栈顶操作符的优先级高于或等于当前操作符时,将栈顶操作符弹出并放入输出栈。
- 将当前操作符压入操作符栈。
- 处理完所有字符后:如果操作符栈中还有操作符,则将它们依次弹出并放入输出栈。
最后,输出栈中的顺序即为后缀表达式。
2-21

D
在栈的操作中,元素是先进后出的。因此,如果一个序列 in 是入栈序列,其对应的出栈序列 out 可以是 in 的倒序。例如,如果入栈顺序是 [1, 2, 3],那么出栈顺序可以是 [3, 2, 1],它们是互为倒序的。
2-22

D
I. 大部分元素已有序:直接插入排序在数据已经基本有序的情况下效率很高。
II. 待排序元素数量很少:直接插入排序在小数据集上的性能优于快速排序,因为它的开销较低。
III. 要求空间复杂度为O(1):直接插入排序是就地排序算法,不需要额外的空间。空间排序的空间复杂度为O(logn)。
IV. 要求排序算法是稳定的:直接插入排序是稳定排序,而快速排序通常不是稳定排序。
多选题
3-1

ABC
面向对象程序设计的三大特性:封装、继承、多态
3-2
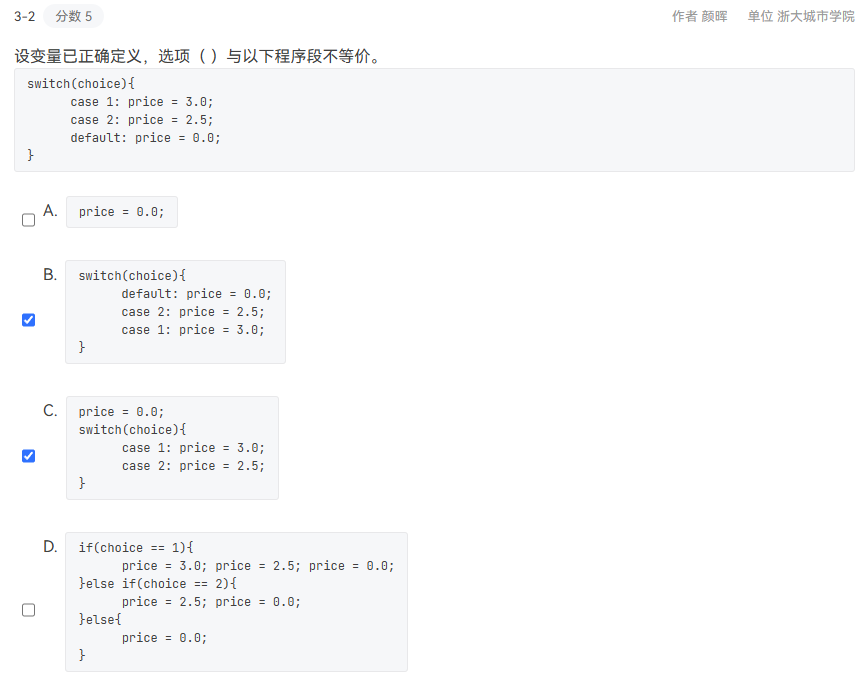
BC
要注意到switch语句中case带有break和不带有break的区别。题目中没有break,不管choice为什么值最后price的值都为0.0。知道了这一点再看各个选项哪个不是使得price始终为0.0的就可以得到答案。
3-3

ABC
A. 自然语言:用日常语言描述算法的步骤,使其容易理解。
B. 伪代码:用类似编程语言的结构来描述算法,方便程序员理解和实现。
C. 流程图:用图形化的方式展示算法的流程和各个步骤之间的关系,直观且清晰。
3-4

ACD
唯一的开始结点和唯一的终端结点(选项A):
- 在非空线性表中,总是有一个开始结点(头结点)和一个终端结点(尾结点)。头结点是表的第一个元素,尾结点是表的最后一个元素。这是线性表的基本特征之一,确保线性表只有一个明确的起点和终点。
不能拥有多个开始结点和多个终端结点(选项B):
- 如果线性表有多个开始结点或者多个终端结点,那么它就不再是一个线性的结构,而可能是树形结构或图形结构。因此,选项B不正确。
每个结点只有一个前驱结点(选项C):
- 除了头结点之外,线性表中的每个结点都只有一个前驱结点。前驱结点指的是在当前结点之前的那个结点。这一特性确保了线性表的每个结点都是有序的。
每个结点只有一个后继结点(选项D):
- 除了尾结点之外,线性表中的每个结点都只有一个后继结点。后继结点指的是在当前结点之后的那个结点。这一特性同样确保了线性表的有序性。
3-5(?)

AC?(貌似是官方答案)
自我观点:
A正确。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
B错误。假设我们有以下二叉树:
A
/ \
B C
\
D
这个二叉树的中序遍历(In-order)序列是:B D A C
这个二叉树的后序遍历(Post-order)序列是:D B C A
在这个二叉树中,节点 B 是某子树的叶子节点,并且在中序遍历序列中,B 是该子树的第一个节点(仅针对左子树来看)。然而,在后序遍历序列中,B 不是该子树的第一个节点,而是 D 才是该子树的第一个节点。
C错误。已知二叉树的前序遍历和后序遍历虽然不能唯一确定树,但是知道树的根节点是哪一个。
D正确。在前序遍历中,根结点首先访问,然后是左子树的所有结点,最后是右子树的所有结点。因此,任何结点的子树的所有结点都直接跟在该结点之后。
3-6

ABE
A. 冒泡排序:冒泡排序在排序过程中只使用了常数级别的额外空间,因此空间复杂度是 O(1)。
B. 选择排序:选择排序同样只需要常数级别的额外空间,用于临时变量交换,因此空间复杂度也是 O(1)。
C. 归并排序:归并排序在合并两个有序序列时需要额外的辅助数组,其空间复杂度是 O(n),而不是 O(1)。
D. 快速排序:快速排序的额外空间复杂度取决于递归调用的深度。最坏的情况下会到达O(n)。一般情况下,快速排序的空间复杂度是 O(log n),但不是 O(1)。
E. 堆排序:堆排序在排序过程中只使用了常数级别的额外空间来维护堆结构,因此空间复杂度是 O(1)。
因此,额外空间复杂度为 O(1) 的排序算法是 A. 冒泡排序、B. 选择排序 和 E. 堆排序。
3-7

ABC
A. 访问第 i 个数据元素:因为链表是线性结构,访问第 i 个元素需要从头结点开始逐个遍历,直到第 i 个元素,因此时间复杂度为 O(n)。
B. 在第 i (1≤i≤n) 个结点后插入一个新结点:在链表中插入一个新结点同样需要先找到第 i 个结点,而找到第 i 个结点的操作需要 O(n) 的时间,因此整体时间复杂度为 O(n)。
C. 删除第 i (1≤i≤n) 个结点:删除某个结点前需要找到该结点,同样需要 O(n) 的时间,因此删除操作的时间复杂度为 O(n)。
D. 将 n 个元素按升序排序:排序操作一般需要 O(n log n) 的时间复杂度,而非 O(n),因此不适用于这个选项。
归调用的深度**。最坏的情况下会到达O(n)。一般情况下,快速排序的空间复杂度是 O(log n),但不是 O(1)。
E. 堆排序:堆排序在排序过程中只使用了常数级别的额外空间来维护堆结构,因此空间复杂度是 O(1)。
因此,额外空间复杂度为 O(1) 的排序算法是 A. 冒泡排序、B. 选择排序 和 E. 堆排序。





















 2026
2026

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








