流式计算中的window机制

已于 2022-07-31 18:00:21 修改
阅读量580 收藏
点赞数
CC 4.0 BY-SA版权
文章标签： 大数据 flink
于 2022-07-30 11:12:36 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/cblock1/article/details/126068747
本文深入探讨了流式计算中的window机制，包括watermark的概念及其在处理乱序数据中的作用，详细介绍了滚动窗口、滑动窗口和会话窗口的原理和应用场景。同时，文章通过两个具体的业务案例展示了如何利用Flink SQL解决实时计算问题，讨论了增量计算和全量计算的差异，以及高级优化策略，如Mini-batch优化、倾斜优化和状态复用等。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

一、摘要

  1. 概述流式计算跟批计算，以及实时数仓和离线数仓的区别；引出流式计算中的window计算定义以及挑战
  2. 介绍实时计算中的Watermark概念，以及如何产生、传递，还有一些典型的生产实践中遇到的问题
  3. 介绍三种最基本的window类型，以及他们的实现原理；同时会结合业务场景介绍一些高级优化的功能和原理
  4. 结合两个真实业务场景的需求，讲解window是如何解决实际生产问题的(字节Flink使用量峰值90亿QPS)
QPS：全名 Queries Per Second，意思是“每秒查询率”，是一台服务器每秒能够响应的查询次数，是对一个特定的查询服务器在规定时间内所处理流量多少的衡量标准

二、概述流式计算机制

简述流式计算的基本概念，与批式计算相比的难点和挑战

    数据价值：实时性越高，数据价值越高

2.1批处理

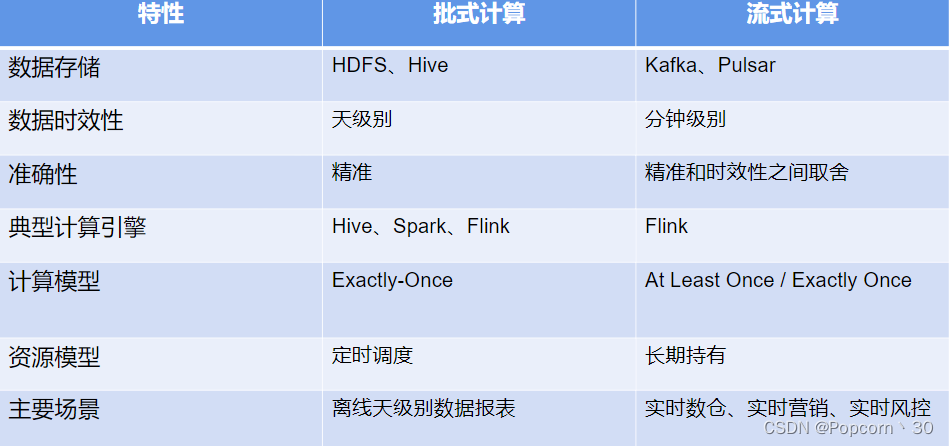
批处理模型典型的数仓架构为T+1架构，即数据计算时天级别的，当天只能看到前一天的计算结果
通常使用的计算引擎为Hive或者Spark等。计算的时候，数据是完全ready的，输入和输出都是确定性的

2.2实时处理

实时计算:处理时间窗口
数据实时流动，实时计算，窗口结束直接发送结果，不需要周期调度任务。

处理时间(Processing time):数据在流式计算系统中真正处理时所在机器的当前时间。
处理时间这是在系统中观察事件的时间
事件时间(Event time):数据产生的时间，比如客户端、传感器、后端代码等上报数据时的时间。
事件时间这是事件实际发生的时间

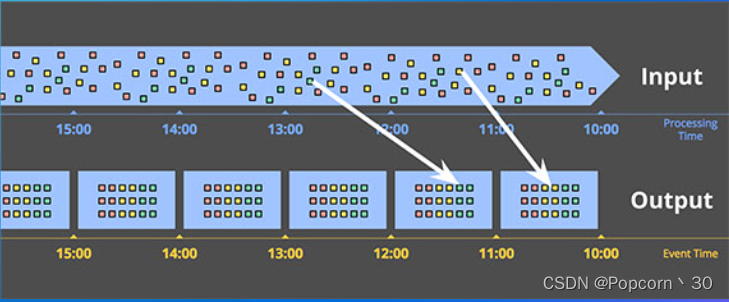
实时计算:事件时间窗口(传入,运算,到输出时间总和)
数据实时进入到真实事件发生的窗口中进行计算，可以有效的处理数据延迟和乱序。

窗口真实结束时间(延迟与乱序)衡量:watermark
在数据中插入—些watermark，来表示当前的真实时间。
在数据存在乱序的时候，watermark就比较重要了，它可以用来在乱序容忍和实时性之间做一个平衡。

三、watermark(水印)

Watermark的含义、生成方法、传递机制，以及—些典型场景的问题和优化

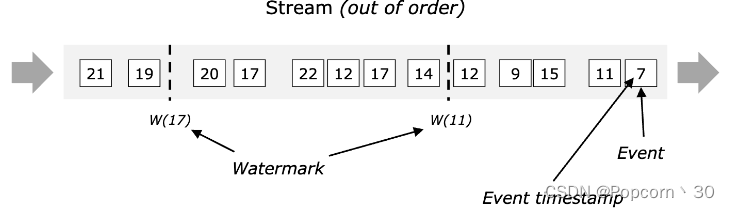
    概念:表示系统认为的当前真实的事件时间

3.1产生watermark

可以通过Watermark Generator 来生成
一般是从数据的事件时间来产生，产生策略可以灵活多样，最常见的包括使用当前事件时间的时

最低0.47元/天 解锁文章

200万优质内容无限畅学
Popcorn丶30
关注
Flink 的 emit 作用
Top5软件工程硕士，先后在京东、字节从事多年Java后端开发、实时和离线大数据开发
04-28 1838
flink 1.9 如下： 配置如下： table.exec.emit.early-fire.enabled：true table.exec.emit.early-fire.delay：60 s early-fire.delay 就是每分钟输出一次结果的意思。 SQL 如下： SELECT TUMBLE_ROWTIME(eventTime, interval ‘1’ day) AS rowtime, dimension, count(distinct id) as uvFROM personG
【Flink实战系列】Flink 的分布式缓存使用
JasonLee实时计算
07-03 1562
Flink提供了一个分布式缓存，类似于Apache Hadoop，可以在本地访问用户函数的并行实例。此函数可用于共享包含静态外部数据的文件，如字典或机器学习的回归模型。 缓存的工作原理如下。程序在其作为缓存文件的特定名称下注册本地或远程文件系统（如HDFS或S3）的文件或目录ExecutionEnvironment。执行程序时，Flink会自动将文件或目录复制到所有工作程序的本地文件系统。用户函...
Flink 理解流式计算中的窗口概念
天道酬勤
11-14 1574
一、描述 Window 是处理无限流的核心。Flink 认为 Batch 是 Streaming 的一个特例，所以 Flink 底层的引擎是一个流式引擎，在上面实现了流处理和批处理。 而窗口（Window）就是从Streaming 到 batch 的一个桥梁。Flink 提供了非常完善的窗口机制，这是 Flink 最大的亮点之一（其他的亮点包括消息乱序处理和 Checkpoint 机制） 二、窗口...
流式计算中的Window机制
m0_51561690的博客
01-04 456
流式计算中的Window机制
PipelineDB流式计算（六）- 滑动窗口
印府的菜园子
12-04 566
目录滑动窗口快速示例滑动聚合失效时间步长因子 滑动窗口 连续视图会随时间持续不断地更新，因此PipelineDB能够结合当前时间来更新连续视图的结果。包含与当前时间相关的时间条件查询称为滑动窗口查询，WHERE子句过滤或接受的事件集会随着时间不断变化。 滑动窗口WHERE子句有两个重要组成部分： clock_timestamp ( )：返回当前时间戳的内置函数。 arrival_timestamp：所有传入事件的一个特殊属性，即，PipelineDB接收它们的时间。 PipelineDB在内部执行此操作，仅
FlinkSQL加参数处理延迟数据
weixin_50034173的博客
10-12 2475
FlinkSQL仅限处理延迟数据，乱序延迟数据最好使用 flinkstream编码解决。
大数据中流式计算中的Window机制
qq_61189986的博客
07-29 519
流式计算VS批式计算 数据价值：实时性越高，数据价值越高 批处理模型典型的数仓架构为T+1架构，即数据计算时天级别的，当天只能看到前一天的计算结果。 通常使用的计算引擎为Hive或者Spark等。...
流式计算-low watermark机制
Move_now的博客
06-24 4676
前言 最近在学习流式计算相关的知识，在阅读了MillWheel论文以及DStream相关实现后，在这里对low watermark机制做一个总结与介绍。 Window 实时数据流是永不停歇的，我们无法获取所有的数据并产出一个最终的结果。很多情况下我们更关心的是最近的状态，而不是从实时数据流启动至今的统计数据。因此需要将数据流切分为一个个片段，这些片段形象的称为Window。总而言之，Wi...
工业物联网中的流式计算
yanboshuju的博客
10-17 952
在设备监控方面，Flink 利用其高效的流处理能力，通过工业物联网统一接入系统实时传来的设备数据，为企业的生产运营提供实时反馈。在事件时间与处理时间的处理上，Flink引入了水印(Watermarks)和时间窗口(Time Window)的概念，允许用户在事件时间语义下进行计算，即使在数据乱序到达的情况下也能保证结果的准确性。首先，在数据模型方面，Flink通过其核心的DataStream API支持流处理，该API基于轻量级的分布式快照算法，可以在保持状态一致性的同时，实现对无界流数据的实时处理。
一文入门大数据准流式计算引擎Spark【万字详解，全网最新】
qq_73181349的博客
09-04 1815
Spark发展、特点、概述，三大组件：Spark Core、Saprk SQL、Spark Streaming，RDD算子、RDD转换和行动操作、RDD持久化和缓存、检查点机制、宽窄依赖、DAG、Stage，Spark SQL发展、概述、特点、dataframe、dataset，Spark Streaming工作机制、缓存、容错、DStream、常见流式计算和离线计算，Spark多种部署方式
Flink 窗口聚合提前触发参数(流和SQL)
延宝小白马的博客
05-22 471
Flink sql 的窗口聚合也可以想 Streaming api 设置 trigger 一样，提前触发计算，并且输出的结果是 upsert 流，会发出 -U/+U 两条数据(输出到 upsert-kafka 就只有 +U 的消息了)
Flink实践：Flink窗口函数在SQL中的使用
Yuan_CSDF的博客
06-17 2616
1.使用FlinkSQL定时输出计算结果： 计算每天的pv,uv，可以开一个24h的窗口，统计窗口内数据情况。但是这样有一个问题，flink sql没有办法直接设置trigger，所以只能等待窗口结束后才会有计算结果输出。这往往不是我们想要的，针对这种情况，有两种解决办法，一种是设置参数，提前输出计算结果；另一种办法是开一分钟窗口（根据自己输出频率来设定窗口）做初步聚合，然后根据日期做二次聚合； 两种方式有一个区别，提前输出方式，因为窗口没有关闭，输出的数据是update，而二次聚合方式，因为窗口已经关
flinkSql 时间窗口到达前 输出结果
jeseva的博客
08-28 2103
flinkSql的时间窗口,可以将一段时间内的数据进行聚合计算. 但是有时, 我们希望可以在时间窗口截止前, 就可以看到结果. 一种方案是: 使用嵌套的时间窗口, 另一种方案是, 在代码进行配置. 我们这里说下如何在代码里进行配置 比如, 时间窗口为 12小时-12小时 (24小时为一个窗口), 但是希望每5分钟就需要输出一次结果. 配置如下: Configuration conf = new Configuration(); conf.setString( "ta
什么是流式(实时)计算?
m0_58873085的博客
06-26 3001
什么是流式计算，流式计算与离线计算的区别，流式计算有哪些概念？流式计算有哪些框架，这些框架多方面性能如何？
大数据系列六：Spark实时流计算-滑动窗口(sliding window)
dustzhu的博客
06-26 1764
一.前言 为什么会有流计算？ 因为有流^_^ 为什么会有流？ 这个原因比较复杂，部分是因为RDBMS解决不了，部分是为了解耦，部分是因为数据价值密度太低…，部分是因为架构^_^ 二.概念 窗口：指定了时间长度和延时长度的时间段（长度也就是时间），比如：长度是5分钟，并且允许有1分钟的延迟。 窗口的创建时间：第一个元素到达就创建。 窗口的销毁时间：在窗口时间长度+延时长度到时。 每个窗口都会绑定一个触发器和一个执行函数，触发器定义了何时会触发窗口的执行函数的计算，比如水位经过了窗口结束时间的时候 窗口产生的目
Storm滑动窗口实现批量计算
sawen21的专栏
03-31 5455
storm是一个流式处理框架，可以做到Spout产生一条数据，Bolt处理一条以达到实时计算。 这种模式并不是实际的业务需要的，我们更多是需要 最近5分钟的PV UV ,最近10分钟的网络最大延迟,最近5分钟页面访问TOP10 这类问题都可以抽象为：每隔M秒统计最近N秒内的数据，即我们需要一个滑动窗口（固定时间段）来控制数据流量 因为storm 未提供api封装，滑动窗口只能自己来实现
Linux环境安装Protobuf
JasonLee实时计算
12-27 403
1,下载地址:https://github.com/protocolbuffers/protobuf/releases最好是下载-all的包,因为里面的依赖文件比较全,不然还需要下载各...
实时计算和流式计算的区别
有志者事竟成
11-17 1万+
实时计算，强调的是实时。比如小明要查看他去年一年的消费总额度，那么当小明点下统计按钮的时候，服务器集群就在噼里啪啦的赶紧计算了，必须在小明能够忍耐的时间范围内得出结果。这种计算的背后实现，一般都是冗余 + 各种高性能部件在做支撑，算法也对实时性做了优化，但实时计算并没有强调用那种算法，只要能保证高实时性的就行。实时计算与离线计算的最大区别，就是离线计算是人无法忍耐的时间进行计算，因此人不需要等待，
流式计算--Kafka详解
热门推荐
ForgetThatNight的博客
03-24 1万+
        理解storm、spark streamming等流式计算的数据来源、理解JMS规范、理解Kafka核心组件、掌握Kakfa生产者API、掌握Kafka消费者API。对流式计算的生态环境有深入的了解，具备流式计算项目架构的能力。所以学习kafka要掌握以下几点： 1、  kafka是什么？ 2、  JMS规范是什么？ 3、  为什么需要消息队列？ 4、  Kafka核心组件 5...
softmax流式计算
最新发布
03-25
### Softmax 的流式计算实现 Softmax 函数是一种常用的激活函数，在机器学习领域广泛应用于分类问题。其核心作用是对输入向量进行指数化处理，并将其归一化为概率分布形式。然而，当面对大规模数据集或实时应用场景时，传统的 softmax 计算可能无法满足性能需求。因此，引入流式计算来优化 softmax 的效率变得尤为重要。 #### 背景知识 在传统 softmax 中，计算过程可以表示为： \[ P(y=i|x) = \frac{e^{z_i}}{\sum_{j=1}^{N} e^{z_j}} \] 其中 \( z_i \) 是第 i 个类别的得分值，\( N \) 表示类别总数。此公式的分母部分涉及全局求和操作，这可能导致高时间复杂度以及内存占用增加的问题。为了应对这一挑战，可以通过以下方式实现流式计算版本的 softmax。 --- #### 方法一：基于滑动窗口的局部规范化 一种常见的策略是采用 **滑动窗口技术** 来近似整个 softmax 输出。具体而言，仅考虑当前时刻及其附近若干步的数据作为上下文范围，从而减少不必要的全局计算开销。 代码示例如下： ```python import numpy as np def streaming_softmax(scores, window_size=5): """ 使用滑动窗口机制实现流式 softmax。 参数: scores (list): 输入分数列表。 window_size (int): 滑动窗口大小，默认为 5。 返回: list: 经过 softmax 处理后的结果。 """ result = [] exp_scores = np.exp(scores) for idx in range(len(exp_scores)): start_idx = max(0, idx - window_size // 2) end_idx = min(len(exp_scores), idx + window_size // 2 + 1) local_sum = sum(exp_scores[start_idx:end_idx]) prob = exp_scores[idx] / local_sum if local_sum != 0 else 0 result.append(prob) return result ``` 这种方法的核心在于通过限定窗口内的元素数量降低每次迭代所需的计算成本[^1]。 --- #### 方法二：增量更新法 另一种更高效的解决方案称为 **增量更新法**，它利用前一步的结果动态调整当前状态下的 softmax 值，而无需重新执行完整的指数运算与归一化步骤。 以下是其实现逻辑： ```python class StreamingSoftmax: def __init__(self): self.cumulative_exp_sum = 0 self.prev_score = None def update(self, new_score): """ 更新 softmax 结果。 参数: new_score (float): 新增项的原始得分。 返回: float: 当前位置对应的 softmax 概率估计。 """ if self.prev_score is not None: # 移除旧项的影响 old_term = np.exp(self.prev_score) self.cumulative_exp_sum -= old_term current_exp = np.exp(new_score) self.cumulative_exp_sum += current_exp probability = current_exp / self.cumulative_exp_sum if self.cumulative_exp_sum != 0 else 0 # 缓存最新一项用于后续移除 self.prev_score = new_score return probability ``` 上述算法假设我们始终维护一个固定长度的历史记录队列，并不断替换最早加入的一项以保持整体结构稳定[^2]。 --- #### 方法三：结合 GPU 加速的大规模分布式实现 如果目标场景涉及到极其庞大的维度或者超多批次样本，则可借助 MATLAB 或其他框架所提供的 GPU 支持功能进一步提升运行效能。例如，在 MATLAB 平台上创建 gpuArray 对象存储中间变量即可自动完成底层硬件调度工作；而在 Python 生态圈里也有类似的库比如 TensorFlow 和 PyTorch 提供相应接口简化开发流程。 下面给出一段伪代码展示如何调用这些工具完成任务： ```python import tensorflow as tf # 初始化设备配置 with tf.device('/GPU:0'): input_tensor = tf.constant([your_data], dtype=tf.float32) output_probs = tf.nn.softmax(input_tensor) ``` 此处需要注意的是实际部署过程中还需要充分考虑到通信延迟等因素影响最终表现效果。 --- ### 总结 综上所述，针对不同业务需求可以选择合适的技术路线达成目的——从小巧灵活适用于嵌入式系统的简单启发式估算方案直到依托先进计算资源驱动的强大端到端流水线架构都有各自适用场合。无论采取哪种途径都应紧密结合项目具体情况权衡利弊做出明智决策。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值