神经网络学习 梯度法的代码实现

import numpy as np
#求梯度
def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 还原值
        it.iternext()   
        
    return grad


def gradient_descent(f,iniy_x,lr=0.01,step_num=100):#
    x=init_x

    for i in range(step_num):
        grad=numercial_gradient(f,x)
        x-=lr*grad

    return x
#设置一个函数
def function_2(x):
    return x[0]**2+x[1]**2
#实现
init_x=np.array([-3.0,4.0])
gradient_descent(function_2,init_x=init_x,lr=0.1,step_num=100)

让我们逐行解释这个代码片段，理解每一行的作用。

1. def gradient_descent(f, init_x, lr=0.01, step_num=100):

这是一个函数定义语句，用来实现梯度下降法。它的作用是最小化输入函数 f，并找到使 f(x) 最小的 x。

• f: 这是目标函数，我们希望通过梯度下降来最小化这个函数。

• init_x: 初始的参数值，即开始时的 x 值。

• lr: 学习率（Learning Rate），默认值为 0.01，控制每次更新步长的大小。

• step_num: 梯度下降的迭代次数，默认值为 100，表示我们将进行 100 次梯度更新。

2. x = init_x

这行代码将初始参数 init_x 赋值给 x，x 是我们在梯度下降中要优化的参数。也就是说，我们开始时的 x 就是 init_x 的值。

3. for i in range(step_num):

这是一个循环，表示梯度下降将迭代 step_num 次。在每一次迭代中，都会计算梯度并更新 x。

• range(step_num) 创建一个迭代器，表示从 0 到 step_num-1 的 100 次迭代。

4. grad = numerical_gradient(f, x)

在每次迭代中，这一行计算目标函数 f 在当前 x 处的梯度。numerical_gradient(f, x) 是计算数值梯度的函数，它会返回 f 对 x 的导数（即梯度）。梯度表示损失函数的变化方向，指示参数应该朝哪个方向调整。

5. x -= lr * grad

这一行根据梯度更新 x 的值，使用标准的梯度下降公式：

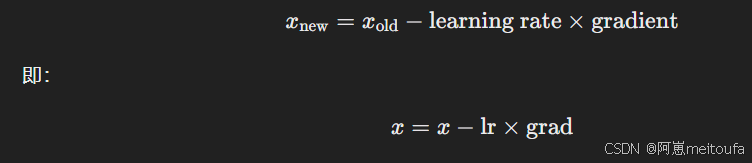
• lr 是学习率，它控制每次更新的步长。

• grad 是梯度，表示在当前点的损失函数沿各个方向的变化率。

通过这一步，x 会向最小化目标函数的方向更新。

6. return x

当迭代结束后，x 会被更新到一个较优值（通常是局部最小值或全局最小值），这时函数返回最终的 x，即我们找到的最优参数。

7. def function_2(x):

这行定义了一个目标函数 function_2(x)，我们希望通过梯度下降法最小化这个函数。目标函数是 x[0]^2 + x[1]^2，也就是二维空间中的一个简单的二次函数。

• 这个函数的最小值出现在 (0, 0) 处，即当 x[0] = 0 和 x[1] = 0 时，f(x) 达到最小值。

8. init_x = np.array([-3.0, 4.0])

这一行创建了一个 NumPy 数组，表示初始参数 x 的值为 [-3.0, 4.0]。这意味着我们从点 (-3.0, 4.0) 开始进行梯度下降。

9. gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)

这行调用了前面定义的 gradient_descent 函数，并传入以下参数：

• function_2: 目标函数，我们要最小化的函数。

• init_x=init_x: 初始值 x，即从 [-3.0, 4.0] 开始。

• lr=0.1: 学习率为 0.1，表示每次更新时的步长为 0.1。

• step_num=100: 梯度下降迭代 100 次。

调用该函数后，梯度下降会开始迭代，更新 x 的值，并最终返回最优的 x（使 function_2 最小化的值）。

总结

这个代码实现了一个简单的梯度下降算法，通过数值计算目标函数的梯度，更新参数 x，从而使目标函数 function_2 达到最小值。整个过程包括初始化 x、计算梯度、更新参数、并返回优化后的 x。