实验-二叉树的应用

• 实验目的

掌握哈夫曼树的基本思想及构造过程，能够对哈夫曼树进行一定的应用，并设计相应的算法。

二、实验内容

输入一组权值，例如{5, 6, 2, 9, 7，8}，构造一颗哈夫曼树，以直观的方式打印该哈夫曼树，并给出各个结点的编码值。二叉树的存储结构定义:

typedef  struct

{  int weght;

   int parent,lch,rch;

}*HuffmanTree;

输入一组权值，例如{5, 6, 2, 9, 7，8}，构造一颗哈夫曼树，以直观的方式打印该哈夫曼树，可分以下层次：

（1）创建哈夫曼树

（2）以左右孩子的身份打印哈夫曼树

（3）以表格的形式打印哈夫曼树

（4）创建哈夫曼树，并以树的形式打印哈夫曼树          

评分标准

（1）实现功能1              50分

（2）实现功能1和2          70分

（3）实现功能1和3          90分

（4）实现功能1和4         100分  

#include <stdio.h>
#include <stdlib.h>

typedef  struct
{
	int weight;
	int parent, lch, rch;
}HuffmanTree;

HuffmanTree* hfTreeInit(int* weight, int length) {
	HuffmanTree* T = (HuffmanTree*)malloc(sizeof(HuffmanTree) * (2 * length - 1));
	//由n个结点形成的哈夫曼树有2n-1个结点
	for (int i = 0; i < length; i++) {
		T[i].weight = weight[i];
		//-1代表没有孩子
		T[i].lch = -1;
		T[i].rch = -1;
		T[i].parent = 0;
	}
	return T;
}
int* selectMin(HuffmanTree* T, int length) {
	int min = 10000;
	int secondMin = 10000;
	int minIndex = 0;
	int secondIndex = 0;
	for (int i = 0; i < length; i++) {
		if (T[i].parent == 0) {
			if (T[i].weight < min) {
				min = T[i].weight;
				minIndex = i;
			}
		}
	}
	for (int i = 0; i < length; i++) {
		if (T[i].parent == 0 && i != minIndex) {
			if (T[i].weight < secondMin) {
				secondMin = T[i].weight;
				secondIndex = i;
			}
		}
	}
	int* res = (int*)malloc(sizeof(int) * 2);//接收索引

	res[0] = minIndex;
	res[1] = secondIndex;
	return res;
}
int creatHuffmanTree(HuffmanTree* T, int length1) {
	int length2 = length1 * 2 - 1;//边界
	int* res;
	int min = -1;
	int secondMin = -1;
	for (int i = length1; i < length2; i++) {
		//因为数组中已经存放了初始的T->length的值,所以下标从T->length开始
		res = selectMin(T, length1);
		//获得索引
		min = res[0];
		secondMin = res[1];
		T[i].weight = T[min].weight + T[secondMin].weight;
		T[i].parent = 0;
		T[min].parent = i;
		T[secondMin].parent = i;
		T[i].lch = min;
		T[i].rch = secondMin;
		length1++;
	}
	return length1;
}
void preOrder(HuffmanTree* T, int index) {
	if (index != -1) {
		//因为树结点都储存在一个数组中,我们通过下标访问,
		printf("%d ", T[index].weight);
		preOrder(T, T[index].lch);
		preOrder(T, T[index].rch);
	}
}
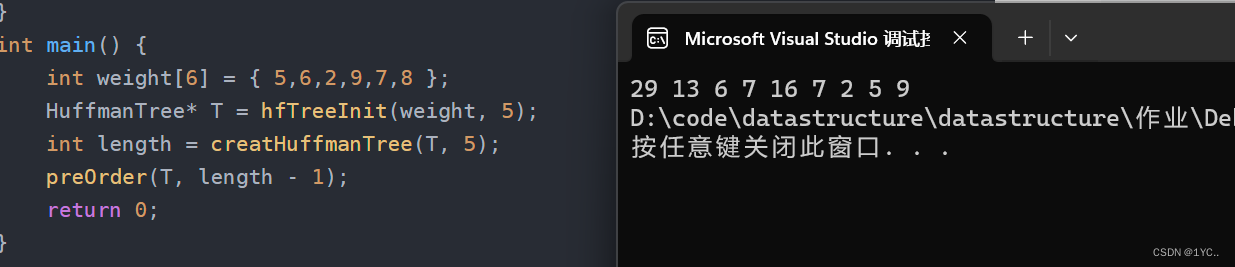
int main() {
	int weight[6] = { 5,6,2,9,7,8 };
	HuffmanTree* T = hfTreeInit(weight, 5);
	int length = creatHuffmanTree(T, 5);
	preOrder(T, length - 1);
	return 0;
}